回帰
注
詳細については、「 テキストと画像 」タブを参照してください。
回帰モデルは、特徴と既知のラベルの両方を含むトレーニング データに基づいて数値ラベル値を予測するようにトレーニングされます。 回帰モデル (または実際には、教師あり機械学習モデル) のトレーニングプロセスには、適切なアルゴリズム (通常はパラメーター化された設定) を使用してモデルをトレーニングし、モデルの予測パフォーマンスを評価し、許容できるレベルの予測精度が得られるまで、さまざまなアルゴリズムとパラメーターでトレーニング プロセスを繰り返してモデルを調整する複数のイテレーションが含まれます。
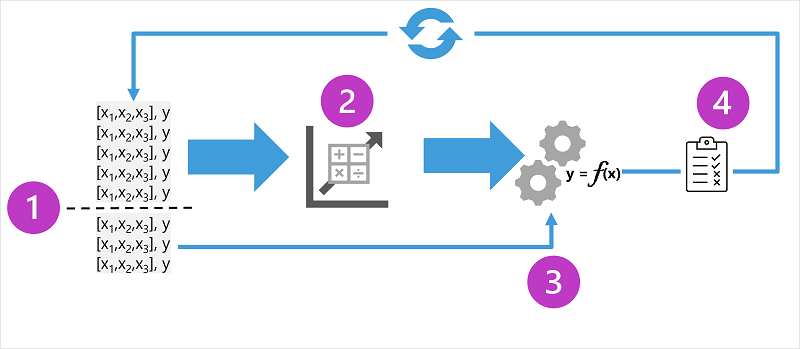
この図は、教師あり機械学習モデルのトレーニング プロセスの 4 つの重要な要素を示しています。
- トレーニング データを (ランダムに) 分割して、トレーニング済みモデルの検証に使用するデータのサブセットを保持しながら、モデルのトレーニングに使用するデータセットを作成します。
- アルゴリズムを使用して、トレーニング データをモデルに適合させます。 回帰モデルの場合は、線形回帰などの回帰アルゴリズムを使用 します。
- 保持した検証データを使用して、特徴のラベルを予測してモデルをテストします。
- 検証データセット内の既知の 実際 のラベルを、モデルが予測したラベルと比較します。 次に、 予測された ラベル値と 実際 のラベル値の差を集計して、検証データに対して予測されたモデルの精度を示すメトリックを計算します。
各トレーニング、検証、および評価のイテレーションの後、許容可能な評価メトリックが達成されるまで、さまざまなアルゴリズムとパラメーターを使用してプロセスを繰り返すことができます。
サンプル - 回帰分析
1 つの特徴値 (x) に基づいて数値ラベル (y) を予測するモデルをトレーニングする、簡略化された例を使用して回帰を調べてみましょう。 ほとんどの実際のシナリオには複数の機能値が含まれており、複雑さが増します。しかし、原則は同じです。
この例では、前に説明したアイスクリームの販売シナリオに取り組みましょう。 この機能では、 温度 を考慮します (値が特定の日の最大温度であると仮定します)。予測するモデルをトレーニングするラベルは、その日に販売されたアイスクリームの数です。 まず、毎日の気温 (x) とアイスクリームの売上 (y) の記録を含むいくつかの履歴データから始めます。

|

|
|---|---|
| 温度 (x) | アイスクリームの販売 (y) |
| 51 | 1 |
| 52 | 0 |
| 67 | 14 |
| 65 | 14 |
| 70 | 23 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 73 | 22 |
| 81 | 30 |
| 78 | 26 |
| 83 | 36 |
回帰モデルのトレーニング
まず、データを分割し、そのサブセットを使用してモデルをトレーニングします。 トレーニング データセットを次に示します。
| 温度 (x) | アイスクリームの販売 (y) |
|---|---|
| 51 | 1 |
| 65 | 14 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 81 | 30 |
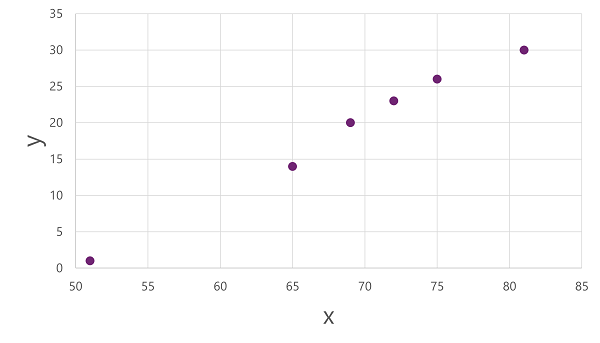
これらの x 値と y 値が相互にどのように関連しているかの分析情報を得るために、次のように 2 つの軸に沿って座標としてプロットできます。
これで、トレーニング データにアルゴリズムを適用し、演算を x に適用して y を計算する関数に合わせる準備ができました。 そのようなアルゴリズムの 1 つは 線形回帰です。これは、次のように、線とプロットされたポイントの間の平均距離を最小限に抑えながら 、x と y の 値の交差部分を通って直線を生成する関数を導き出すことによって機能します。
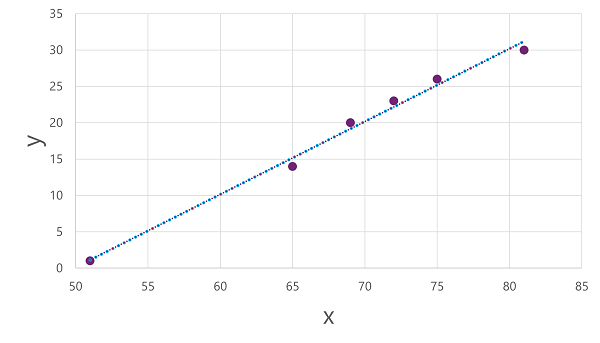
線は、線の傾きが x の特定の値の y の値を計算する方法を記述する関数の視覚的表現です。 線は x 軸を 50 で切片するので、 x が 50 の場合、 y は 0 になります。 プロット内の軸マーカーからわかるように、線は傾き、 x 軸に沿って 5 を増やすたびに y 軸の上に 5 が増加します。したがって、 x が55の場合、 y は5です。 x が 60 の場合、 y は 10 です。 x の指定された値に対して y の値を計算するには、関数は単に 50 を減算します。つまり、関数は次のように表現できます。
f(x) = x-50
この関数を使用すると、任意の温度で 1 日に販売されるアイスクリームの数を予測できます。 たとえば、天気予報で、明日は 77 度になるとします。 モデルを適用して 77 から 50 を計算し、明日 27 個のアイスクリームを販売すると予測できます。
しかし、私たちのモデルはどのくらい正確ですか?
回帰モデルの評価
モデルを検証し、予測の程度を評価するために、ラベル (y) 値がわかっているデータを保持しました。 保持しているデータを次に示します。
| 温度 (x) | アイスクリームの販売 (y) |
|---|---|
| 52 | 0 |
| 67 | 14 |
| 70 | 23 |
| 73 | 22 |
| 78 | 26 |
| 83 | 36 |
このモデルを使用して、特徴 (x) 値に基づいて、このデータセット内の各観測値のラベルを予測できます。予測ラベル (ŷ) を既知の実際のラベル値 (y) と比較します。
前にトレーニングしたモデル ( 関数 f(x) = x-50 をカプセル化) を使用すると、次の予測が行われます。
| 温度 (x) | 実績売上 (y) | 予測売上 (ŷ) |
|---|---|---|
| 52 | 0 | 2 |
| 67 | 14 | 十七 |
| 70 | 23 | 20 |
| 73 | 22 | 23 |
| 78 | 26 | 28 |
| 83 | 36 | 33 |
次のように、 予測ラベル と 実際 のラベルの両方を特徴値に対してプロットできます。
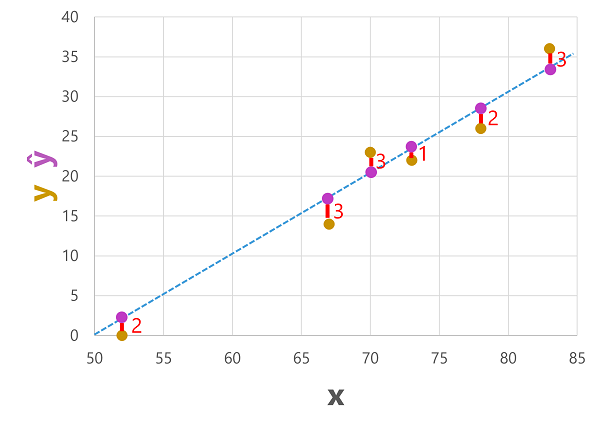
予測されたラベルはモデルによって計算されるため、関数行に配置されますが、関数によって計算される ŷ 値と検証データセットの実際の y 値の間に多少の差異があります。これは、予測が実際の値からどれだけ離れていたかを示す ŷ と y の 値の間の線としてプロットに示されます。
回帰評価メトリック
予測値と実際の値の違いに基づいて、回帰モデルの評価に使用される一般的なメトリックをいくつか計算できます。
平均絶対誤差 (MAE)
この例の分散は、各予測が間違っていたアイスクリームの数によって示されます。 予測が実際の値 を超えている か 下 にあるかは関係ありません (たとえば、-3 と +3 はどちらも分散 3 を示します)。 このメトリックは、各予測の 絶対誤差 と呼ばれ、検証セット全体について 平均絶対誤差 (MAE) として要約できます。
アイスクリームの例では、絶対誤差 (2、3、3、1、2、3) の平均 (平均) は 2.33 です。
平均二乗誤差 (MSE)
平均絶対誤差メトリックでは、予測ラベルと実際のラベルの間のすべての不一致が均等に考慮されます。 ただし、エラーが少ないが大きいモデルよりも、一貫して間違っているモデルを少量使用する方が望ましい場合があります。 個々の誤差を 二乗 し、二乗値の平均を計算することによって、より大きな誤差を「増幅」するメトリックを生成する方法の 1 つ。 このメトリックは、 平均二乗誤差 (MSE) と呼ばれます。
このアイスクリームの例では、2 乗絶対値 (4、9、9、1、4、9) の平均は 6 です。
二乗平均平方根誤差 (RMSE)
平均二乗誤差はエラーの大きさを考慮に入れるのに役立ちますが、エラー値が 2 乗 するため、結果のメトリックはラベルによって測定された量を表すのではありません。 言い換えると、モデルの MSE は 6 ですが、誤って予測されたアイスクリームの数の観点からはその精度は測定されません。6 は、検証予測の誤差レベルを示す数値スコアにすぎません。
アイスクリームの数の観点から誤差を測定する場合は、MSEの 平方根 を計算する必要があります。これは、当然ながら 、平方根平均二乗誤差と呼ばれるメトリックを生成します。 この場合、√6 は 2.45 (アイスクリーム) です。
決定係数 (R2)
ここまでのすべてのメトリックは、モデルを評価するために、予測された値と実際の値の不一致を比較します。 しかし、実際には、モデルが考慮するアイスクリームの毎日の売上には自然なランダム分散があります。 線形回帰モデルでは、トレーニング アルゴリズムは、関数と既知のラベル値の間の平均分散を最小限に抑える直線に適合します。 決定係数 (より一般的には R 2 またはR-2と呼ばれます) は、検証データのいくつかの異常な側面 (たとえば、地元の祭りのために非常に異常な数のアイスクリームの販売がある日) とは対照的に、モデルで説明できる検証結果の分散の割合を測定するメトリックです。
R2 の計算は、前のメトリックよりも複雑です。 次のように、予測ラベルと実際のラベルの 2 乗差の合計と、実際のラベル値と実際のラベル値の平均の 2 乗差の合計を比較します。
R2 = 1- ∑(y-ŷ)2 ÷ ∑(y-ȳ)2
それが複雑に見える場合は、あまり心配しないでください。ほとんどの機械学習ツールでは、メトリックを計算できます。 重要な点は、モデルによって説明される分散の割合を表す 0 ~ 1 の値になります。 簡単に言うと、この値が 1 に近いほど、モデルが検証データに適合する方が適しています。 アイスクリーム回帰モデルの場合、検証データから計算されるR2 は 0.95 です。
反復トレーニング
上記のメトリックは、回帰モデルの評価に一般的に使用されます。 ほとんどの実際のシナリオでは、データ サイエンティストは反復的なプロセスを使用して、モデルのトレーニングと評価を繰り返し行います。次に示す内容はさまざまです。
- 特徴の選択と準備(モデルに含める特徴を選び、それらに対して精度を向上させるための計算を行うこと)。
- アルゴリズムの選択 (前の例では線形回帰を調べていましたが、他にも多くの回帰アルゴリズムがあります)
- アルゴリズム パラメーター (アルゴリズムの動作を制御するための数値設定。x パラメーターと y パラメーターを区別するためにハイパーパラメーターと呼ばれます)。
複数のイテレーションの後、特定のシナリオで許容できる最適な評価メトリックを得るモデルが選択されます。