二項分類

完了

回帰と同様に、分類は 教師あり 機械学習手法です。そのため、モデルのトレーニング、検証、評価の同じ反復プロセスに従います。 回帰モデルのような数値を計算する代わりに、分類モデルのトレーニングに使用されるアルゴリズムはクラス割り当ての 確率 値を計算し、モデルのパフォーマンスを評価するために使用される評価メトリックは、予測されたクラスと実際のクラスを比較します。

二項分類 アルゴリズムは、1 つのクラスに対して考えられる 2 つのラベルの 1 つを予測するモデルをトレーニングするために使用されます。 基本的に、true または false を予測 します。 ほとんどの実際のシナリオでは、モデルのトレーニングと検証に使用されるデータ観測値は、複数の特徴 (x) 値と 1 または 0 の y 値で構成されます。

例 - 二項分類

二項分類のしくみを理解するために、1 つの特徴 (x) を使用してラベル y が 1 か 0 かを予測する簡略化された例を見てみましょう。 この例では、患者の血糖値を使用して、患者に糖尿病があるかどうかを予測します。 モデルをトレーニングするデータを次に示します。

血糖値 (x)	糖尿病ですか？ (y)
67	0
103	1
114	1
72	0
116	1
65	0

二項分類モデルのトレーニング

モデルをトレーニングするには、アルゴリズムを使用して、クラス ラベルが true になる確率 (つまり、患者が糖尿病を持っている) を計算する関数にトレーニング データを適合させます。 確率は 0.0 ~ 1.0 の値として測定され、すべての可能なクラスの合計確率は 1.0 になります。 たとえば、糖尿病の患者の確率が 0.7 の場合、患者が糖尿病でない確率は 0.3 になります 。

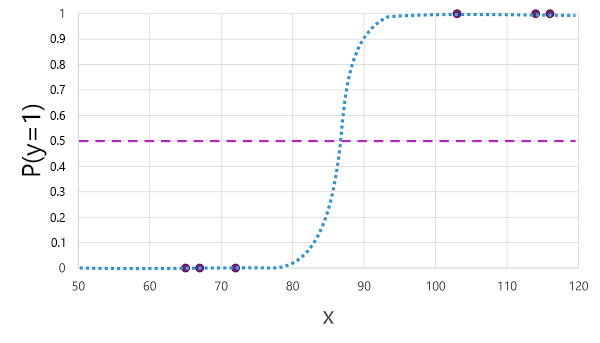
0.0 から 1.0 の値を持つシグモイド (S 字形) 関数を派生させるロジスティック回帰など、二項分類に使用できるアルゴリズムは多数あります。次に例を示します。

注

その名前にもかかわらず、機械学習 のロジスティック回帰では、回帰 ではなく分類に使用されます。 重要な点は、生成する関数の ロジスティック 特性です。これは、低い値と上位の値の間の S 字曲線 (二項分類に使用する場合は 0.0 と 1.0) を表します。

アルゴリズムによって生成される関数は、指定された値 x に対して y が true (y=1) になる確率を記述します。 数学的には、次のように関数を表現できます。

f(x) = P(y=1 | x)

トレーニング データ内の 6 つの観測のうち 3 つの場合、 y は確実に 当てはまることがわかっています。したがって、 y= 1 が 1.0 であり、他の 3 つの観測値の確率は y が確実 に false であることを知っているので、 y=1 は 0.0 です。 S 字曲線は、線上に x の値をプロットして 、y が 1 である対応する確率を識別するように確率分布を記述します。

この図には、この関数に基づくモデルが true (1) または false (0) を予測するしきい値を示す水平線も含まれています。 しきい値は、 y (P(y) = 0.5) の中間点にあります。 この時点以上の値の場合、モデルは true (1) を予測します。この時点より下の値の場合は false (0) を予測します。 たとえば、血糖値が 90 の患者の場合、関数の確率値は 0.9 になります。 0.9 が 0.5 のしきい値より高いため、モデルは true (1) を予測します。つまり、患者は糖尿病であると予測されます。

二項分類モデルの評価

回帰と同様に、二項分類モデルをトレーニングするときは、トレーニング済みのモデルを検証するためのデータのランダムなサブセットを保持します。 糖尿病分類器を検証するために、次のデータを保持したとします。

血糖値 (x)	糖尿病ですか？ (y)
66	0
107	1
112	1
71	0
87	1
89	1

前に派生したロジスティック関数を x 値に適用すると、次のプロットになります。

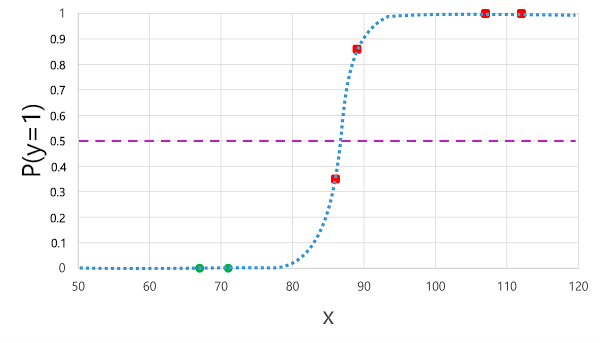
関数によって計算される確率がしきい値を上回っているか下回っているかに基づいて、モデルは各観測値に対して 1 または 0 の予測ラベルを生成します。 次に示すように、 予測された クラス ラベル (ŷ) と 実際 のクラス ラベル (y) を比較できます。

血糖値 (x)	実際の糖尿病診断 (y)	予測の糖尿病診断 (ŷ)
66	0	0
107	1	1
112	1	1
71	0	0
87	1	0
89	1	1

二項分類評価メトリック

二項分類モデルの評価メトリックを計算する最初の手順は、通常、考えられる各クラス ラベルの正しい予測と正しくない予測の数のマトリックスを作成することです。

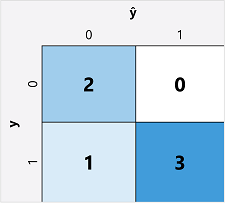
この視覚化は 混同行列と呼ばれ、予測の合計が次の場所に表示されます。

• ŷ=0 および y=0: 真の陰性 (TN)
• ŷ=1 および y=0: 偽陽性 (FP)
• ŷ=0 および y=1: 偽陰性 (FN)
• ŷ=1 および y=1: 真陽性 (TP)

混同行列の配置は、正しい (true) 予測が左上から右下の斜線に表示されるようにします。 多くの場合、色の強度は各セルの予測数を示すために使用されるため、よく予測されるモデルをひとめで確認すると、深く網掛けされた対角線の傾向が明らかになります。

精度

混同行列から計算できる最も簡単なメトリックは 、正確さ (モデルが正しく取得した予測の割合) です。 精度は次のように計算されます。

(TN+TP) ÷ (TN+FN+FP+TP)

糖尿病の例では、次の計算が行われます。

(2+3) ÷ (2+1+0+3)

= 5 ÷ 6

= 0.83

検証データでは、糖尿病分類モデルによって 83% の確率で正しい予測が生成されました。

精度は、最初はモデルを評価するための適切なメトリックのように見えるかもしれませんが、これを考慮してください。 人口の 11% が糖尿病であるとします。 常に0を予測するモデルを作成でき、その際、特徴を評価して患者を区別しようとする実際の試みを行わなくても、89%の精度を達成できます。 実際に必要なのは、肯定的なケースの場合は 1 、負のケースでは 0 を予測する際のモデルのパフォーマンスをより深く理解することです。

取り消し

再現率 は、モデルが正しく識別した肯定的なケースの割合を測定するメトリックです。 つまり、糖尿病を 持つ 患者の数と比較して、モデルは糖尿病を持っていると 予測 した人はいくつでしたか?

取り消しの数式は次のとおりです。

TP ÷ (TP + FN)

糖尿病の例:

3 ÷ (3 +1)

= 3 ÷ 4

= 0.75

そこで我々のモデルは,糖尿病患者の75% を糖尿病と正しく同定した.

精度

精度 は、再現率と同様のメトリックですが、真のラベルが実際に正である予測される肯定的なケースの割合を測定します。 言い換えると、モデルによって 予測される 患者の割合は、実際に糖尿病を 持っている のでしょうか?

精度の数式は次のとおりです。

TP ÷ (TP+FP)

糖尿病の例:

3 ÷ (3 +0)

= 3 ÷ 3

= 1.0

そこで、私たちのモデルによって予測された患者の100% は、実際に糖尿病を持っています。

F1 スコア

F1 スコア は、再現率と精度を組み合わせた全体的なメトリックです。 F1 スコアの数式は次のとおりです。

(2 x 精度 x 再現率) ÷ (精度 + 再現率)

糖尿病の例:

(2 x 1.0 x 0.75) ÷ (1.0 + 0.75)

= 1.5 ÷ 1.75

= 0.86

曲線の下の領域 (AUC)

再現率のもう 1 つの名前は真陽性率 (TPR) であり、FP÷(FP+TN) として計算される偽陽性率 (FPR) と呼ばれる同等のメトリックがあります。 しきい値 0.5 を使用する場合のモデルの TPR は 0.75 であり、FPR の数式を使用して 0÷2 = 0 の値を計算できることは既にわかっています。

もちろん、モデルが true (1) と予測するしきい値を変更すると、正と負の予測の数に影響します。したがって、TPR と FPR のメトリックを変更します。 これらのメトリックは、多くの場合、0.0 から 1.0 の間のすべての可能なしきい値の TPR と FPR を比較する 受信演算子特性 (ROC) 曲線をプロットしてモデルを評価するために使用されます。

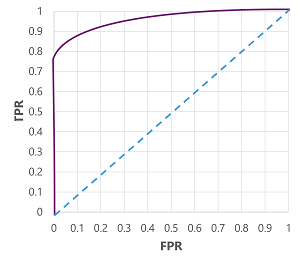
完璧なモデルの ROC 曲線は、左側の TPR 軸をまっすぐ上に、次に上部の FPR 軸を横切ります。 曲線のプロット エリアは 1x1 を測定するため、この完璧な曲線の下の面積は 1.0 になります (つまり、モデルは時間の 100% 正しいことを意味します)。 一方、左下から右上の斜線は、バイナリ ラベルをランダムに推測することによって達成される結果を表します。0.5の曲線下の面積を生成します。 言い換えると、2 つの可能なクラス ラベルを指定すると、50% の時間を正しく推測することが合理的に期待できます。

糖尿病モデルの場合、上記の曲線が生成され、 曲線下面積 (AUC) メトリックは 0.875 です。 AUCは0.5より高いため、モデルはランダムに推測するよりも患者が糖尿病を持っているかどうかを予測する方が優れていると結論付けることができます。