PRT 数式 (Direct3D 9)

PRT を実装するシェーダーを完全に理解するには、シェーダーが出口放射を計算するために使用する数式を派生させるのが役立ちます。

最初に、次の式は、任意の離れた照明を持つ拡散オブジェクト上の直接照明に起因する出口放射輝度を計算する一般的な方程式です。

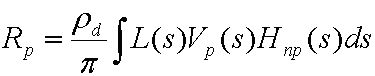
どこ：

パラメーター	形容
Rp	頂点 p での終了放射。 メッシュ上のすべての頂点で評価されます。
pd	サーフェスのアルベド。
円周率	省エネ正規化係数として使用される定数。
L(s)	照明環境 (ソースの放射)。
Vp₍s₎	ポイント p のバイナリ可視性関数。 ポイントが光を見ることができる場合は 1、見えない場合は 0 です。
Hnp₍s₎	ランバートの法則のコサイン用語。 max((Np· s)、0 に等しい。Np はポイント p のサーフェス法線です。
s	球の上に統合される変数。

 

球面調和などの球面基底関数を使用して、次の式は照明環境に近似します。

照明環境の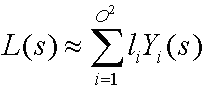

どこ：

パラメーター	形容
L(s)	照明環境 (ソースの放射)。
私	基底関数の数を合計する整数。
O	球面高調波の順序。
li	係数。
Yi(s)	球に対する何らかの基底関数。

 

これらの係数 L' のコレクションは、基底関数 Y を持つ関数 L の最適な近似値を提供します。 置換および分散すると、次の式が生成されます。

l を置換し、式

Y_i(s)Vp₍s₎Hnp₍s₎ の積分は、シミュレーターがメッシュ上のすべての頂点に対して事前計算する pi 転送係数 t です。 これを代入すると、次の式が生成されます。

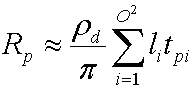に置換した後の出口放射輝度の式

これをベクター表記に変更すると、次の非圧縮方程式が生成され、各チャネルの終了放射輝度が計算されます。

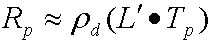
どこ：

パラメーター	形容
Rp	頂点 p での終了放射。
pd	サーフェスのアルベド。
L'	lのベクトルは、球面調和基底関数へのソース放射の射影である。 これは球面調和係数の order² ベクトルです。
トイレットペーパー	頂点 p の order² 転送ベクトル。 シミュレーターは、転送係数を p で除算します。

 

これらのベクトルはどちらも球面調和係数の order² ベクトルであるため、これは単なるドット積であることに注意してください。 順序によっては、ドットが高価になる可能性があるため、圧縮を使用できます。 クラスター化プリンシパル コンポーネント分析 (CPCA) と呼ばれるアルゴリズムは、データを効率的に圧縮します。 これにより、より高次の球面調和近似を使用できるため、影が鮮明になります。

CPCA は、転送ベクトルを近似する次の式を提供します。

近似転写ベクトル式

どこ：

パラメーター	形容
トイレットペーパー	頂点 p の転送ベクトル。
Mk	クラスター k の平均。
j	PCA ベクトルの数を合計する整数。
N	PCA ベクトルの数。
pj	ポイント p の j 番目の PCA の重み。
Bkj	クラスター k の jth PCA 基底ベクトル。

 

クラスターは、同じ平均ベクトルを共有する頂点の数にすぎません。 クラスター平均、PCA 重み、PCA 基底ベクトル、頂点のクラスター ID を取得する方法については、以下で説明します。

これらの 2 つの数式を置き換えると、次の結果が得られます。

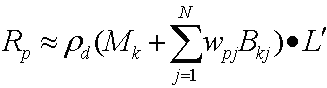に置換した後の終了放射の式

次に、ドット積を分配すると、次の式が生成されます。

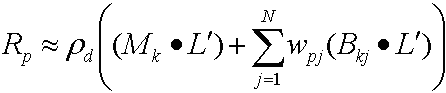を分散した後の出口放射度の式

両方 (Mk·L') および (B_kj·L') は頂点ごとに定数であり、サンプルは CPU を使用してこれらの値を計算し、定数として頂点シェーダーに渡します。各頂点_pj 変更されるため、サンプルでは頂点ごとのデータが頂点バッファーに格納されます。

関連トピック

事前計算された放射転送