이 문서에서는 Grover 알고리즘이 작동하게 하는 수학 원칙에 대한 자세한 이론적 설명을 찾을 수 있습니다.
수학 문제를 해결하기 위한 Grover 알고리즘의 실제 구현은 Grover의 검색 알고리즘 구현을 참조하세요.
문제 설명
Grover 알고리즘은 구조화되지 않은 데이터 검색(또는 검색 문제)에 대한 솔루션을 가속화하여 클래식 알고리즘보다 적은 단계로 검색을 실행합니다. 모든 검색 작업은 검색 항목 $x$를 허용하는 추상 함수 $f(x)$로 표현할 수 있습니다. 항목 $x$가 검색 작업의 솔루션인 경우 $f(x)=1$입니다. $x$ 항목이 솔루션이 아니면 $f(x)=0$입니다. 검색 문제는 f(x_0)$1$과 같은 $x_0= 항목을 $찾는 것으로 구성됩니다.
x$$지정된 값이 유효한 솔루션인지 여부를 확인할 수 있는 모든 문제(&따옴표; 예 또는 문제 없음&따옴표;) 은 검색 문제의 관점에서 공식화할 수 있습니다. 예는 다음과 같습니다.
- 부울 만족도 문제: 부울 값 집합이 지정된 부울 수식을 충족하나요?
- 여행 세일즈맨 문제: 모든 도시를 연결하는 가장 짧은 루프는 무엇인가요?
- 데이터베이스 검색 문제: 데이터베이스 테이블에 x$$레코드가 포함되어 있나요?
- 정수 인수 분해 문제: 숫자 $N$ 가 숫자 $x$로 나눠지나요?
Grover의 알고리즘이 해결하려는 작업은 다음과 같이 표현할 수 있습니다. 주어진 클래식 함수 $f(x):\{0,1\}^n \rightarrow\{0,1\}$, 여기서 $n$은 검색 공간의 비트 크기입니다. $f(x_0)$1$에 해당하는 입력 =x_0$을 찾습니다. 알고리즘의 복잡성은 $f(x)$ 함수 사용의 횟수로 측정됩니다. 고전적으로 최악의 시나리오 $에서는 f(x)$ 를 총 $N-1$ 번 평가해야 합니다. 여기서 $N=2^n$은 모든 가능성을 시험해 봅니다. N-1$ 요소 후에$는 마지막 요소여야 합니다. Grover의 양자 알고리즘은 이 문제를 훨씬 빠르게 해결할 수 있어, 알고리즘의 속도를 제곱적으로 향상시킵니다. 여기서 이차식은 대략 N$\sqrt{ 평가만 필요하다는 것을 암시하며, 이는 대안적으로 }$N$$ 평가 (아마도 이차형) 이 필요할 것에 비해 간단한 것입니다.
알고리즘 개요
검색 작업에 적합한 $N=2^n$개의 항목이 있다고 가정하고, 각 항목은 $0$부터 $N-1$까지의 정수로 할당되어 인덱싱됩니다. 또한 $M$개의 서로 다른 유효한 입력이 있다고 가정합니다. 이는 $f(x)$1$에 해당하는 =M$개의 입력이 있음을 의미합니다. 알고리즘의 단계는 다음과 같습니다.
- $ $n$\ket{0}$개 큐비트로 구성된 레지스터를 $ 상태로 초기화합니다.
- 레지스터의 각 큐비트에 $H$를 적용하여 레지스터를 균일한 중첩으로 준비합니다. $$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
- 레지스터 $N에 다음 작업을 {\text{최적의}}$ 횟수만큼 적용합니다.
- 조건부 위상 이동 -1을 솔루션 항목에 적용하는 위상 오라클$O_f$.
- 레지스터의 각 큐비트에 H$를 적용$합니다.
- $\ket{0}$을 제외한 모든 계산 기반 상태에 $$-1의 조건부 위상 변화를 적용. 유니터리 연산 $-O_0$은 오직 $ 조건부 위상 편이를 나타내는 $O_0$\ket{0}$으로 나타낼 수 있습니다.
- 레지스터의 각 큐비트에 H$를 적용$합니다.
- 레지스터를 측정하여 확률이 매우 높은 솔루션인 항목의 인덱스 가져오기
- 유효한 솔루션인지 확인합니다. 그렇지 않은 경우 다시 시작합니다.
최적의 $N_{\text{}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{{2}\right\r바닥$은 레지스터를 측정하여 올바른 항목을 얻을 가능성을 최대화하는 최적의 반복 횟수입니다.
참고
3.b, 3.c 및 3.d 단계의 공동 적용은 일반적으로 Grover의 확산 연산자로 알려져 있습니다.
레지스터에 적용되는 전체 단위 작업은 다음과 같습니다.
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
레지스터의 상태를 단계별로 따라갑니다.
프로세스를 설명하기 위해 큐비트가 2개뿐이고 유효한 요소가 $\ket{01}인 간단한 경우에 대해 레지스터 상태의 수학적 변환을 수행해 보겠습니다.$
레지스터는 다음 상태에서 시작됩니다.
$$\ket{\text{등록}}=\ket{{00}$$
각 큐비트에 $H$ 적용한 후 레지스터의 상태가 다음과 같이 변환됩니다.
$$\ket{\text{레지스터}}=\frac{{1}{\sqrt{4}}\sum_{\lbrace 0,1 \in \r중괄호}^2\ket{}=\frac12(\ket{00}+\ket{01}+\ket{{10}+\ket{11})$$
그러면 위상 오라클이 적용되어 다음과 같은 결과를 얻습니다.
$$\ket{\text{register}}=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
그런 다음 $H$이 각 큐비트에 다시 한 번 작용하여 다음을 제공합니다.
$$\ket{\text{등록}}=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$
이제 조건부 단계 이동은 $\ket{00}$제외한 모든 상태에 적용됩니다.
$$\ket{\text{레지스터}}=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$
마지막으로, 첫 번째 Grover 반복은 $H$을 다시 적용함으로써 종료됩니다.
$$\ket{\text{등록}}=\ket{{01}$$
위의 단계를 수행하면 유효한 항목이 단일 반복에서 발견됩니다. 나중에 보겠지만, N=4와 단일 유효한 항목에 대해 최적의 반복 횟수는 $N_{\text{최적의}}=1$입니다.
기하학적 설명
Grover의 알고리즘이 작동하는 이유를 확인하려면 기하학적 관점에서 알고리즘을 연구해보겠습니다. $M$ 유효한 솔루션이 있다고 가정하면, 검색 문제에 대한 해결 방법이 않는 모든 양자 상태의 중첩입니다.
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
모든 상태의 중첩은 검색 문제에 대한 해결책입니다.
$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
좋은 및 나쁜는 항목이 유효하거나 유효하지 않을 수는 없기 때문에, 상호 배타적인 집합으로 상태는 서로 독립적입니다. 두 상태 모두 벡터 공간에서 평면의 직교 기초를 형성합니다. 이 평면을 사용하여 알고리즘을 시각화할 수 있습니다.
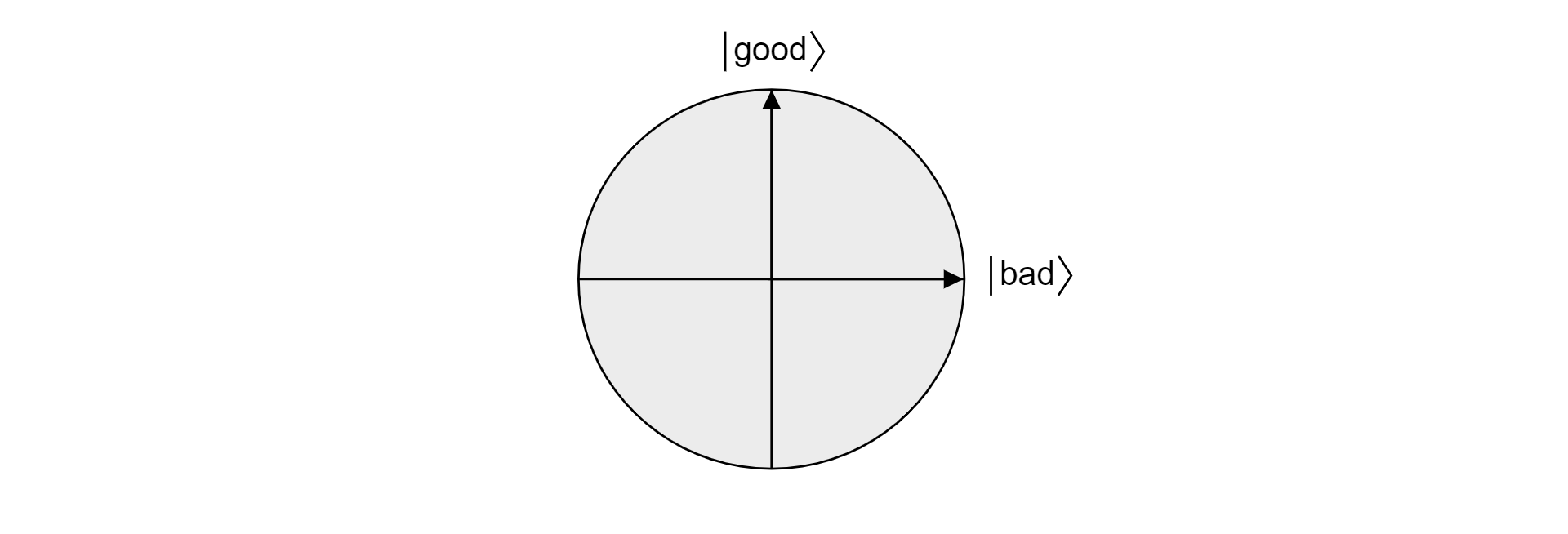
이제 $\ket{\psi}$가 $\ket{\text{좋고}}$$\ket{\text{나쁨}}$으로 확장된 평면에 존재하는 임의의 상태라고 가정해 보겠습니다. 해당 평면에 있는 모든 상태는 다음과 같이 표현할 수 있습니다.
$$\ket{\psi} = \alpha \ket{\text{좋음}} + \beta\ket{\text{나쁨}}$$
$\alpha$와 $\beta$는 실수입니다. 이제 리플렉션 연산자 $R_{\ket{\psi}}$ 소개해 보겠습니다. 여기서 $\ket{\psi}$ 는 평면에 있는 큐비트 상태입니다. 연산자는 다음과 같이 정의됩니다.
$$ {\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$
$\ket{\psi}$ 방향에 대한 리플렉션은 $\ket{\psi}$ 방향에 대한 리플렉션으로 기하학적으로 해석될 수 있기 때문에 리플렉션 연산자 $\ket{\psi}$라고 합니다. 이를 보려면 $\ket{\psi}$과 그 직교 여공간 $\ket{\psi^{\perp}}$로 형성된 평면의 직교 기저를 사용합니다. 평면의 모든 상태 $\ket{\xi}$ 는 다음과 같이 분해할 수 있습니다.
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
$연산자 R_{\ket{\psi}}$을 $\ket{\xi}$에 적용하는 경우:
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
연산자 $R_{\ket{\psi}}$는 $\ket{\psi}$에 직교하는 구성 요소를 반전하지만, $\ket{\psi}$ 구성 요소는 그대로 둡니다. 따라서 $R_{\ket{\psi}}$ 에 대한 $\ket{\psi}$리플렉션입니다.
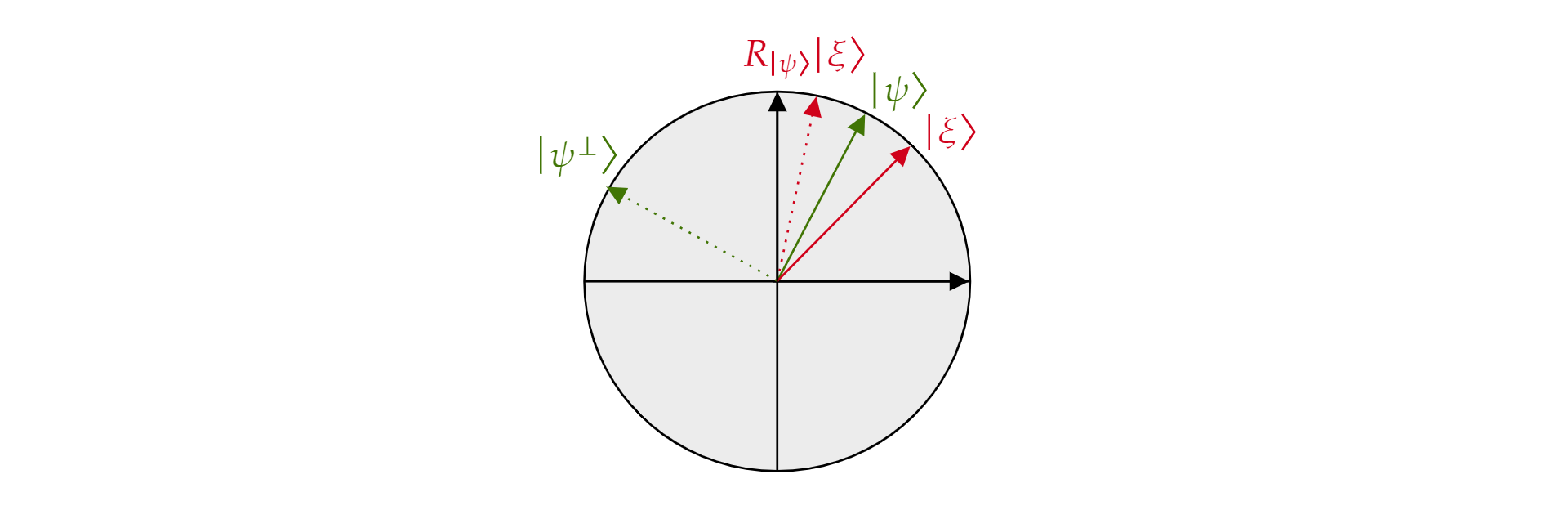
Grover의 알고리즘은 모든 큐비트에 $H$를 처음 적용한 후 모든 상태의 균일한 중첩을 시작합니다. 다음과 같이 작성할 수 있습니다.
$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
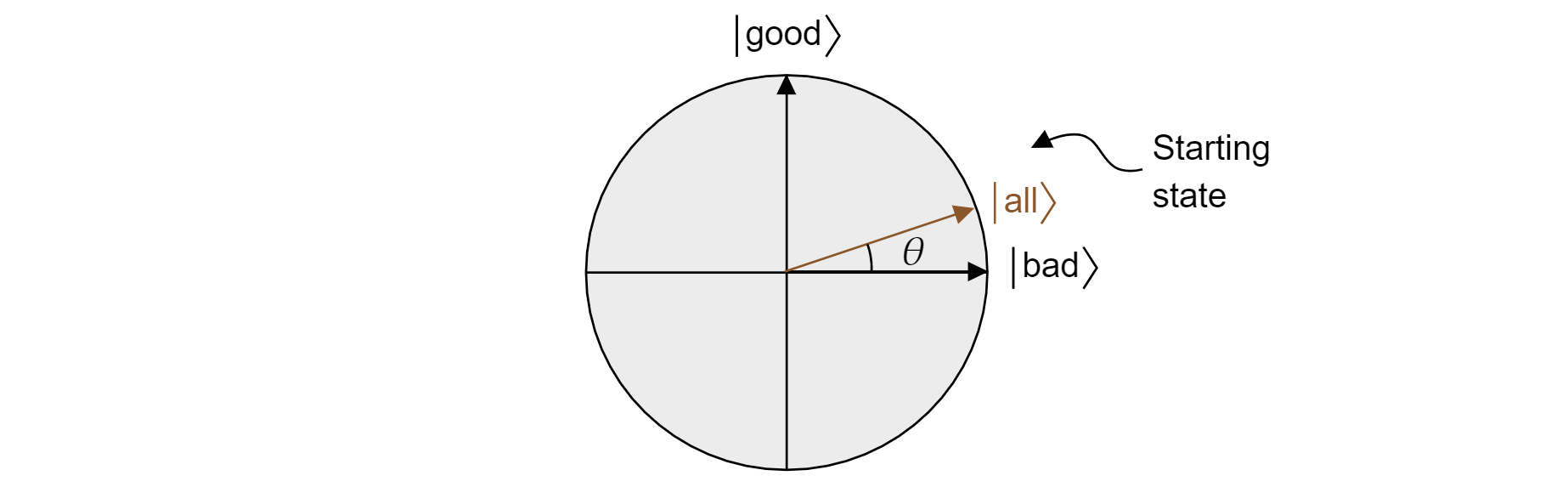
따라서 국가는 비행기에 살고있다. 동등한 중첩 상태에서 측정할 때 올바른 결과를 얻을 확률은 $|\bra{\text{good}}\ket{\text{all}}|^2=M/N$에 불과하며, 이는 임의 추측에서 기대할 수 있는 것입니다.
Oracle $O_f$는 검색 문제에 대한 솔루션에 부정적 단계를 추가합니다. 따라서 잘못된$\ket{\text{ 축에 대한 }}$리플렉션으로 작성할 수 있습니다.
$$O_f = R_{\ket{\text{나쁜}}}= 2\ket{\text{나쁜}}\bra{\text{나쁜}} - \mathbb{I}$$
마찬가지로 조건부 위상 편이 $O_0$은 상태 $\ket{0}$에 대한 반전된 리플렉션일 뿐입니다.
$$O_{0}= R_{\ket{0}}= -2\ket{{0}\bra{{0} + \mathbb{I}$$
이 사실을 알고 있으면 Grover 확산 연산 $-H^{\otimes n} O_{0} H^{\otimes n}$ 상태 $\ket{모든}$에 대한 리플렉션인지 쉽게 확인할 수 있습니다. 다음을 수행합니다.
$$-H^{\otimes n} O_{{0} H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathbb{I}H^{\otimes n}= 2\ket{\text{모든}}\bra{\text{모든}} - \mathbb{I}= R_{\ket{\text{모든}}}$$
Grover 알고리즘의 각 반복은 두 개의 리플렉션 $R_{\ket{\text{bad}}}$ 및 $R_{\ket{\text{all}}}$의 구성임을 입증했습니다.
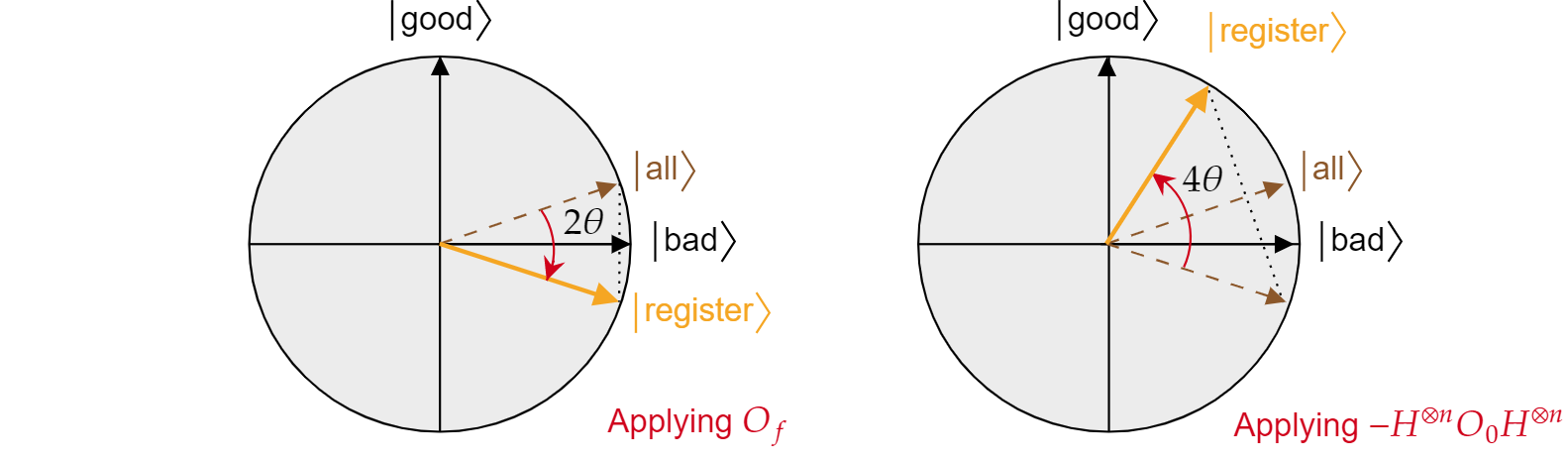
각 Grover 반복의 결합된 효과는 각도 $2\theta$의 시계 반대 방향으로 회전하는 것입니다. 다행히 각도 $\theta$는 찾기가 쉽습니다. $\theta$는 $\ket{\text{all}}$과 $\ket{\text{bad}}$ 사이의 각도일 뿐이므로 스칼라 제품을 사용하여 각도를 찾을 수 있습니다. \cos\theta$가 모두{잘못된 것으로 알려져 }=\braket{\text{있으므로 모든}|\text{나쁜}}$$\braket{\text{ 값을 계산}|\text{해야 합니다.}}$ 모두를 나쁜 것과 좋은 것의 관점에서 분해하면, 다음과 같이 결론지을 수 있습니다:
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
레지스터 상태와 $\ket{\text{좋은}}$ 상태 사이의 각도는 반복할 때마다 감소하여 유효한 결과를 얻을 가능성이 높아집니다. 이 확률을 계산하려면 $|\braket{\text{register}|\text{^2}}|의 값을 계산$하기만 하면 됩니다. $\ket{\text{양호한}}$ 및 $\ket{\text{레지스터}}$ 사이의 각도는 $\gamma(k)$로 표현됩니다. 여기서 $k$는 반복 횟수입니다.
$$\gamma = \frac{\pi}{2}-\theta -2k\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
따라서 성공 확률은 다음과 같습니다.
$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
최적의 반복 수
성공 확률은 반복 횟수의 함수로 작성할 수 있으므로 성공 확률 함수를 대략 최대화하는 가장 작은 양의 정수를 계산하여 최적 반복 횟수 $N_{\text{optimal}}$을 찾을 수 있습니다.
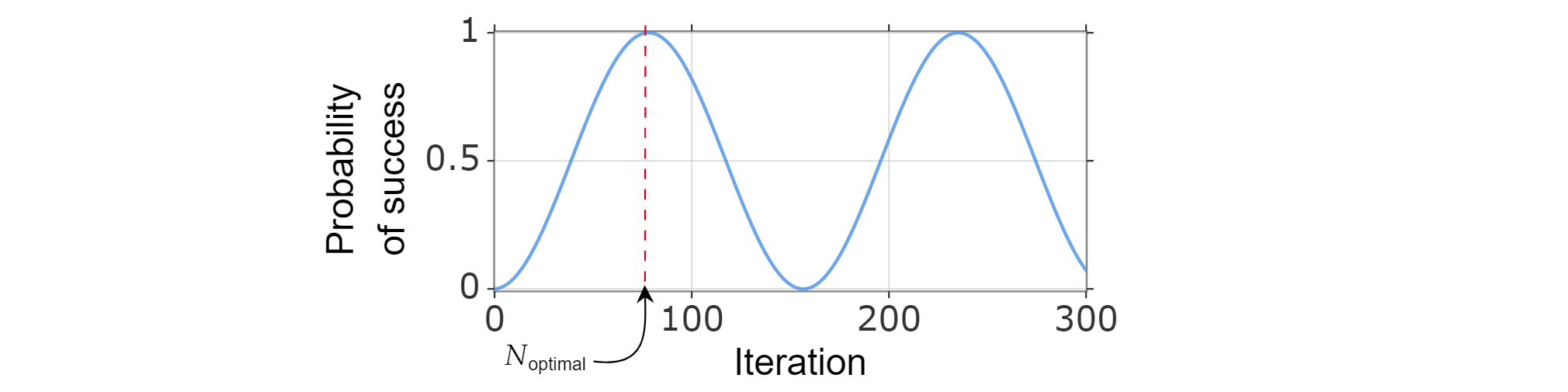
알려진 바에 따르면 $\sin^2{x}$가 $x=\frac{\pi}{2}$에 대해 첫 번째 최댓값에 도달하므로:
$$\frac{\pi}{{2}=(2k_{\text{최적}} +1)\arccos \left(\sqrt{\frac{N-M}{N}}\right)$$
다음과 같습니다:
$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$
마지막 단계에서 $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.
따라서 $N_{\text{최적}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{{2}\right\rfloor$를 선택할 수 있습니다.
복잡성 분석
이전 분석에서 유효한 항목을 찾기 위해 oracle $O_f\left의 \sqrt{\frac{O}{(}}\rightN$M$)$ 쿼리가 필요합니다. 그러나 시간 복잡성 측면에서 알고리즘을 효율적으로 구현할 수 있나요? $O_0$는 n$비트에 대한 부울 연산을 계산하는 것을 기반으로 하며, O(n)$ 게이트를 사용하여 구현할 수 있는 것으로 알려져 있습니다.$ 또한 Hadamard 게이트의 두 계층이 있으며, 이는 $n$ 개의 Hadamard 게이트로 구성되어 있습니다. 따라서 이러한 두 구성 요소는 반복당 O(n)$ 게이트만 $필요합니다. $N=2^n$이므로 O(n)$O(log(N))=를 따릅니다$. 따라서 $O\left(\sqrt{\frac{N}{M}}\right)$ 반복과 반복당 $O(log(N))$개의 게이트가 필요한 경우, oracle 구현을 고려하지 않은 총 시간 복잡도는 $O\left(\sqrt{\frac{N}{M}}log(N)\right)$입니다.
알고리즘의 전반적인 복잡성은 궁극적으로 oracle $O_f$ 구현의 복잡성에 따라 달라집니다. 함수 평가가 기존 컴퓨터보다 양자 컴퓨터에서 훨씬 더 복잡한 경우, 기술적으로는 더 적은 쿼리를 사용하더라도 전체 알고리즘 런타임은 양자 사례에서 더 길어집니다.
참조
Grover 알고리즘에 대한 학습을 계속하려면 다음 원본 중에서 확인할 수 있습니다.
- 로브 케이 그로버의 오리지널 논문
- 닐슨, M. A. & 추앙, I. L. (2010). 양자 검색 알고리즘 섹션. 양자 계산 및 양자 정보.
- Arxiv.org Grover 알고리즘