확률 함수 평가

아티클
05/06/2019

중요

Machine Learning Studio(클래식)에 대한 지원은 2024년 8월 31일에 종료됩니다. 해당 날짜까지 Azure Machine Learning으로 전환하는 것이 좋습니다.

2021년 12월 1일부터 새로운 Machine Learning Studio(클래식) 리소스를 만들 수 없습니다. 2024년 8월 31일까지는 기존 Machine Learning Studio(클래식) 리소스를 계속 사용할 수 있습니다.

ML Studio(클래식)에서 Azure Machine Learning으로 기계 학습 프로젝트 이동에 대한 정보를 참조하세요.
Azure Machine Learning에 대한 자세한 정보.

ML Studio(클래식) 설명서는 사용 중지되며 나중에 업데이트되지 않을 수 있습니다.

지정된 확률 분포 함수를 데이터 집합 맞추기

범주: 통계 함수

참고

적용 대상: Machine Learning Studio(클래식) 전용

유사한 끌어서 놓기 모듈은 Azure Machine Learning 디자이너에서 사용할 수 있습니다.

모듈 개요

이 문서에서는 Machine Learning Studio(클래식)에서 확률 평가 함수 모듈을 사용하여 Bernoulli, Pareto 또는 Poisson 분포와 같은 열의 분포를 설명하는 통계 측정값을 계산하는 방법을 설명합니다.

이 모델을 사용하려면 숫자 값 열이 하나 이상 포함된 데이터 세트를 연결하고 테스트할 확률 분포를 선택합니다. 모듈은 지정된 확률 함수의 값을 포함하는 데이터 테이블을 반환합니다.

선택한 확률 분포에 대해 다음 값을 계산할 수 있습니다.

누적 분포 함수(cdf)
역 누적 분포 함수(InverseCdf)
확률 밀도 함수(Pdf)

확률 분포가 유용한 이유는 무엇인가요?

확률 분포에 대해 데이터를 평가할 때 알려진 속성이 있는 값 집합에 대해 열 값을 매핑합니다. 데이터가 이러한 잘 알려진 배포 중 하나에 해당하는지 여부를 알면 데이터의 다른 속성을 유추할 수 있습니다. 일반적으로 데이터에 가장 적합한 분포를 식별할 수 있으면 모델에서 더 나은 예측을 얻을 수 있습니다.

사용할 확률 분포 함수는 측정 중인 데이터와 변수에 따라 달라집니다. 예를 들어 일부 분포는 불연속 값의 확률을 설명하도록 설계되었습니다. 다른 변수는 연속 숫자 변수에만 사용하기 위한 것입니다. 일부 분포의 경우 예상되는 평균, 자유도 등을 미리 알고 있어야 합니다. 자세한 내용은 지원되는 확률 분포를 참조하세요.

확률 평가 함수를 구성하는 방법

모든 옵션은 계산할 확률 분포의 유형에 따라 변경됩니다. 확률 분포 방법을 변경하면 다른 선택 항목이 다시 설정됩니다.

따라서 먼저 배포 옵션을 선택해야 합니다.
입력으로 사용되는 데이터 세트에는 숫자 데이터가 포함되어야 합니다. 다른 형식의 데이터는 무시됩니다.
각 분석에 대해 단일 확률 분포 방법을 적용할 수 있습니다. 다른 확률 분포를 계산하려면 테스트하려는 각 배포에 대해 모듈의 별도 인스턴스를 추가합니다.

실험에 확률 평가 함수 모듈을 추가합니다. 이 모듈은 Machine Learning Studio(클래식)의 통계 함수 범주에서 찾을 수 있습니다.
하나 이상의 숫자 열이 포함된 데이터 세트를 커넥트.
분포 옵션을 사용하여 계산할 확률 분포 종류를 선택합니다. 옵션 목록 및 필요한 인수 는 지원되는 확률 분포 를 참조하세요.
분포에 필요한 모든 매개 변수를 설정합니다.
만들 세 가지 통계 중 하나를 선택합니다. 누적 분포 함수(cdf), 역 누적 분포 함수(InverseCdf) 또는 확률 밀도 함수(pdf).

정의는 기술 정보 섹션 을 참조하세요.
열 선택기를 사용하여 선택한 확률 분포를 계산할 열을 선택합니다.
- 선택한 모든 열에는 숫자 데이터 형식이 있어야 합니다.
- 열의 데이터 범위도 선택한 확률 함수에 유효해야 합니다. 그렇지 않으면 오류가 발생하거나 NaN 결과가 반환됩니다.
- 스파스 열의 경우에는 백그라운드 0에 해당하는 모든 값이 처리되지 않습니다.
결과 모드 옵션을 사용하여 결과를 출력하는 방법을 지정합니다. 열 값을 확률 분포 값으로 바꾸거나 데이터 집합에 새 값을 추가하거나 확률 분포 값만 반환할 수 있습니다.
실험을 실행하거나 확률 함수 평가 모듈을 마우스 오른쪽 단추로 클릭하고 선택한 실행을 클릭합니다.

결과

다음 표에는 Forest Fires 샘플 데이터 세트의 단일 온도 열에 추가 옵션을 사용하는 결과의 예가 포함되어 있습니다.

temp	StandardNormal.Cdf(temp)	StandardNormal.Pdf(temp)	FFisher.cdf(temp	FFisher.cdf(temp
8.2	1	1	0.984774	0.004349
18	1	1	0.997896	0.000311
14.6	1	1	0.996352	0.000648
8.3	1	1	0.985201	0.004187
11.4	1	1	0.993147	0.001502

생성된 열의 머리글에는 사용된 확률 분포가 포함됩니다.

데이터에 적합한 확률 분포를 잘 모르는 경우 모든 숫자 열에 대한 누적 분포 및 확률 밀도의 빠른 차트를 만들 수 있습니다.

데이터 세트 또는 모듈 출력을 마우스 오른쪽 단추로 클릭하고 시각화를 선택합니다.
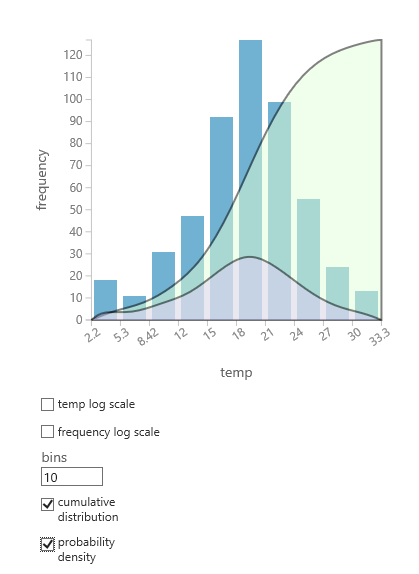
관심 있는 열을 선택하고 히스 토그램 창에서 누적 분포 또는 확률 밀도를 선택합니다.
분포의 차트는 다음과 같이 데이터를 나타내는 히스토그램에 겹쳐집니다.

aml_histogram_cdf_pdf_chart

지원되는 확률 분포

확률 평가 함수 모듈은 다음 분포를 지원합니다.

베르누이

Bernoulli 분포는 이진 값에 대한 분포입니다. 즉, 두 값만 가능한 경우 예상되는 분포를 모델화합니다.

계산하려면 Bernoulli를 선택하고 다음 옵션을 설정합니다.

성공 확률
매개 변수 p 는 1이 생성될 확률을 지정합니다. 성공 확률을 지정하는 0.0 ~ 1.0 사이의 숫자(float)를 입력합니다. 기본값은 0.5입니다.

베타

베타 분포는 연속 단변량 분포입니다.

계산하려면 베타를 선택하고 다음 옵션을 설정합니다.

셰이프
분포의 셰이프를 변경할 값을 입력합니다.

셰이프 매개 변수는 위치나 크기를 정의하지 않는 확률 분포의 모든 매개 변수입니다. 따라서 셰이프의 값을 입력하면 매개 변수가 분포를 이동하거나 늘리거나 줄이지 않고 분포의 모양을 변경합니다.

값은 숫자(double)여야 합니다. 기본값은 1.0입니다.
크기 조정
분포의 크기 조정에 사용할 숫자를 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
상한
분포의 상한을 나타내는 숫자(double)를 입력합니다. 기본값은 1.0입니다.
하한
분포의 하한을 나타내는 숫자(double)를 입력합니다. 기본값은 0.0입니다.

이항

이항 분포는 불연속 일변량 분포입니다. 이항 분포는 샘플의 성공 수를 모델링하는 데 사용됩니다. 샘플링 시에는 대체가 사용됩니다. 대체가 없는 샘플링의 경우에는 초기하 분포를 사용합니다.

계산하려면 이항을 선택하고 다음 옵션을 설정합니다.

성공 확률
성공 확률을 나타내는 0.0 ~ 1.0 사이의 숫자(float)를 입력합니다. 기본값은 0.5입니다.
시행 횟수
시행 횟수를 지정합니다.

최소값이 integer1인 값을 사용합니다. 기본값은 3입니다.

코시

코시 분포는 대칭 연속 확률 분포입니다.

계산하려면 Cauchy를 선택하고 다음 옵션을 설정합니다.

위치
0^번째 요소의 위치를 나타내는 숫자(double)를 입력합니다.

위치 매개 변수의 값을 지정하여 소수 자리수의 위아래로 확률 분포를 이동할 수 있습니다.

기본값은 0.0입니다.

카이 제곱

카이 제곱 분포는 k 독립적, 표준, 보통, 임의 변수의 제곱의 합계입니다.

계산하려면 ChiSquare를 선택하고 다음 옵션을 설정합니다.

자유도 수 숫자(double)를 입력하여 자유도를 지정합니다. 기본값은 1.0입니다.

ChiSquareRightTailed

이 옵션은 오른쪽 꼬리 카이 제곱 분포를 제공합니다.

계산하려면 ChiSquareRightTailed를 선택하고 다음 옵션을 설정합니다.

자유도 개수
자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 1.0입니다.

지수

지수 분포는 음이 아닌 한 매개 변수로 매개 변수가 지정된 실수 분포입니다.

계산하려면 지수를 선택하고 다음 옵션을 설정합니다.

Lambda
람다 매개 변수로 사용할 숫자(double)를 입력합니다. 기본값은 1.0입니다.

FFisher

피셔 F 분포라고도 하는 샘플에 대한 Fisher 통계의 확률을 생성합니다. 이 분포는 양측입니다.

계산하려면 FFisher를 선택하고 다음 옵션을 설정합니다.

분자의 자유도입니다.
분자에 사용된 자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 3.0입니다.
분모의 자유도입니다.
분모에 사용된 자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 6.0입니다.

FFisherRightTailed

오른쪽 꼬리 피셔 분포를 만듭니다. Fisher 분포는 Fisher F-분포, Snedecor 분포 또는 Fisher-Snedecor 분포라고도 합니다. 이 분포는 우측 형식입니다.

계산하려면 FFisherRightTailed를 선택하고 다음 옵션을 설정합니다.

분자의 자유도입니다.
분자에 사용된 자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 3.0입니다.
분모의 자유도입니다.
분모에 사용된 자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 6.0입니다.

감마

감마 분포는 두 개의 매개 변수가 있는 연속 확률 분포군입니다. 예를 들어, 카이 제곱은 감마 분포의 특수 사례입니다.

계산하려면 감마를 선택하고 다음 옵션을 설정합니다.

크기 조정
분포의 크기 조정에 사용할 값을 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
위치
0^번째 요소의 위치를 나타내는 숫자(double)를 입력합니다.

위치 매개 변수의 값을 지정하여 소수 자리수의 위아래로 확률 분포를 이동할 수 있습니다.

기본값은 0.0입니다.

GeneralizedExtremeValues

극한 값을 처리하도록 개발된 배포를 만듭니다. GEV(일반화된 극단 값) 분포는 실제로 감벨, 프레셰 및 와이블 분포(유형 I, II 및 II 극단 값 분포라고도 함)를 결합하는 연속 확률 분포 그룹입니다.

극단적 인 가치 이론에 대한 자세한 내용은 위키 백과에서이 문서를 참조하십시오: 피셔 티펫 - Gnedenko 정리.

계산하려면 GeneralizedExtremeValues를 선택하고 다음 옵션을 설정합니다.

셰이프
분포의 셰이프를 변경할 값을 입력합니다.

셰이프 매개 변수는 위치나 크기를 정의하지 않는 확률 분포의 모든 매개 변수입니다. 따라서 셰이프의 값을 입력하면 매개 변수가 분포를 이동하거나 늘리거나 줄이지 않고 분포의 모양을 변경합니다.

값은 숫자(double)여야 합니다. 기본값은 1.0입니다.
크기 조정
분포의 크기 조정에 사용할 값을 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
위치
0^번째 요소의 위치를 나타내는 숫자(double)를 입력합니다.

위치 매개 변수의 값을 입력하여 소수 자리수의 위아래로 확률 분포를 이동할 수 있습니다.

기본값은 0.0입니다.

기하

기하학적 분포는 하나의 양수로 매개 변수가 있는 양의 정수에 대한 분포입니다.

계산하려면 기하 도형을 선택하고 다음 옵션을 설정합니다.

성공 확률
성공 확률을 나타내는 0.0 ~ 1.0 사이의 숫자(float)를 입력합니다. 기본값은 0.5입니다.

참고

이 기하학적 분포 구현은 0을 생성하지 않습니다.

GumbelMax

감벨 분포는 여러 극단 값 분포 중 하나입니다. GumbelMax 옵션은 최대 극단 값 유형 1 분포를 구현합니다.

계산하려면 GumbelMax를 선택하고 다음 옵션을 설정합니다.

크기 조정
분포의 크기 조정에 사용할 값을 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
위치
0^번째 요소의 위치를 나타내는 숫자(double)를 입력합니다.

위치 매개 변수의 값을 입력하여 소수 자리수의 위아래로 확률 분포를 이동할 수 있습니다.

기본값은 0.0입니다.

GumbelMin

감벨 분포는 여러 극단 값 분포 중 하나입니다. 감벨 분포는 SEV(최소 극단 값) 분포 또는 최소 극단 값(유형 1) 분포라고도 합니다. GumbelMin 옵션은 최소 극한 값 형식 1 분포를 구현합니다.

계산하려면 GumbelMin을 선택하고 다음 옵션을 설정해야 합니다.

크기 조정
분포의 크기 조정에 사용할 값을 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
위치
0^번째 요소의 위치를 나타내는 숫자(double)를 입력합니다.

위치 매개 변수의 값을 입력하여 소수 자리수의 위아래로 확률 분포를 이동할 수 있습니다.

기본값은 0.0입니다.

초기하

이항 분포에서 대체를 사용한 그리기 성공 횟수를 설명하는 것처럼 하이퍼지메트릭 분포는 대체하지 않고 유한 모집단에서 n개 그리기 시퀀스의 성공 횟수를 설명하는 불연속 확률 분포입니다.

계산하려면 Hypergeometric을 선택하고 다음 옵션을 설정합니다.

샘플 수
사용할 샘플 수를 나타내는 정수를 입력합니다. 기본값은 9입니다.
성공 수
성공 값을 정의하는 정수를 입력합니다. 기본값은 24입니다.
모집단 크기
초기하 분포 예측 시 사용할 모집단 크기를 지정합니다.

라플라스

Laplace 분포는 실수에 대한 분포이며 평균 및 배율 매개 변수로 매개 변수화됩니다.

계산하려면 Laplace 분포를 선택하고 다음 옵션을 설정합니다.

크기 조정
분포의 크기 조정에 사용할 값을 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
위치
0^번째 요소의 위치를 나타내는 숫자(double)를 입력합니다.

위치 매개 변수의 값을 입력하여 소수 자리수의 위아래로 확률 분포를 이동할 수 있습니다.

기본값은 0.0입니다.

로지스틱

로지스틱 분포는 정규 분포와 비슷하지만 분포 왼쪽에 제한이 없습니다. 로지스틱 분포는 로지스틱 회귀 및 신경망 모델에 사용하며 생명 과학 데이터를 모델링하는 데 사용합니다.

계산하려면 로지스틱을 선택하고 다음 옵션을 설정합니다.

크기 조정
분포의 크기 조정에 사용할 값을 입력합니다.

분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

기본값은 1.0입니다. 값은 양수여야 합니다.
평균값
분포의 예상 평균 값을 표시하는 숫자(double)를 입력합니다. 기본값은 0.0입니다.

LogNormal

LogNormal 분포는 연속 단변량 분포입니다.

계산하려면 Lognormal을 선택하고 다음 옵션을 설정합니다.

평균값
분포의 예상 평균 값을 나타내는 숫자(double)를 입력합니다. 기본값은 0.0입니다.
표준 편차
분포의 예상 표준 편차를 표시하는 양수(double)를 입력합니다. 기본값은 1.0입니다.

NegativeBinomial

음 이항 분포는 r, p의 두 매개 변수를 사용하는 자연수에 대한 분포입니다. 정수인 특수한 경우 r 머리의 확률이 p일 때 r^th 헤드 앞의 꼬리 수로 분포를 해석할 수 있습니다.

계산하려면 NegativeBinomial을 선택하고 다음 옵션을 설정합니다.

성공 확률
성공 확률을 나타내는 0.0 ~ 1.0 사이의 숫자(float)를 입력합니다. 기본값은 0.5입니다.
성공 수
성공 값을 지정하는 정수를 입력합니다. 기본값은 24입니다.

보통

일반 분포를 가우시안 분포라고도 합니다.

계산하려면 Normal을 선택하고 다음 옵션을 설정합니다.

평균값
분포의 예상 평균 값을 나타내는 숫자(double)를 입력합니다. 기본값은 0.0입니다.
표준 편차
분포의 예상 표준 편차를 표시하는 양수(double)를 입력합니다. 기본값은 1.0입니다.

파레토

파레토 분포는 사회, 과학, 지구 물리학, 보험 통계 및 여러 다른 유형의 관찰 가능한 현상에 부합하는 멱법칙 확률 분포입니다.

계산하려면 Pareto를 선택하고 다음 옵션을 설정합니다.

셰이프
분포의 셰이프를 변경할 값(선택 사항)을 입력합니다.

셰이프 매개 변수는 위치나 크기를 정의하지 않는 확률 분포의 모든 매개 변수입니다. 따라서 셰이프의 값을 입력하면 매개 변수가 분포를 이동하거나 늘리거나 줄이지 않고 분포의 모양을 변경합니다.

값은 숫자(double)여야 합니다. 기본값은 1.0입니다.
크기 조정
값(선택 사항)을 입력하여 분포의 배율을 변경합니다. 분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

값은 숫자(double)여야 합니다. 기본값은 1.0입니다.

포아송

이 구현에서는 크누스의 방법을 사용하여 포아송 분포 확률 변수를 생성합니다. 포아송 분포에 대한 자세한 내용은 포아송 회귀를 참조하세요.

계산하려면 Poisson을 선택하고 다음 옵션을 설정합니다.

평균값
분포의 예상 평균 값을 나타내는 숫자(double)를 입력합니다. 기본값은 0.0입니다.

레일리

레일리 분포는 연속 확률 분포입니다. 이 분포가 발생하는 방법의 예로, 2차원 풍속 벡터의 구성 요소가 비상관이며 일반적으로 등분산으로 분포되어 있는 경우 풍속은 레일리 분포를 나타냅니다.

계산하려면 Rayleigh를 선택하고 다음 옵션을 설정합니다.

하한
분포의 하한을 나타내는 숫자(double)를 입력합니다. 기본값은 0.0입니다.

StandardNormal

이 옵션은 다른 매개 변수 없이 표준 정규 분포를 제공합니다.

계산하려면 StandardNormal을 선택하고 열을 선택합니다.

TStudent

이 옵션은 단변 학생의 t 분포를 구현합니다.

계산하려면 TStudent를 선택하고 다음 옵션을 설정합니다.

자유도 개수
자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 1.0입니다.

TStudentRightTailed

하나의 우측을 사용하여 단변량 스튜던트 t-분포를 구현합니다.

계산하려면 TStudentRightTailed를 선택하고 다음 옵션을 설정합니다.

자유도 개수
자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 1.0입니다.

TStudentTwoTailed

양측 스튜던트 t-분포를 구현합니다.

계산하려면 TStudentTwoTailed를 선택하고 다음 옵션을 설정합니다.

자유도 개수
자유도를 지정하는 숫자(double)를 입력합니다. 기본값은 1.0입니다.

Uniform

균일 분포는 평등 분포라고도 합니다.

계산하려면 Uniform을 선택하고 다음 옵션을 설정합니다.

하한
분포의 하한을 나타내는 숫자(double)를 입력합니다. 기본값은 0.0입니다.
상한
분포의 상한을 나타내는 숫자(double)를 입력합니다. 기본값은 1.0입니다.

와이블

와이블 분포는 신뢰성 공학에 널리 사용되며, Shape 매개 변수를 사용하여 다른 많은 배포를 모델링할 수 있습니다.

계산하려면 Weibull을 선택하고 다음 옵션을 설정합니다.

셰이프
분포의 셰이프를 변경할 값(선택 사항)을 입력합니다.

셰이프 매개 변수는 위치나 크기를 정의하지 않는 확률 분포의 모든 매개 변수입니다. 따라서 셰이프의 값을 입력하면 매개 변수가 분포를 이동하거나 늘리거나 줄이지 않고 분포의 모양을 변경합니다.

값은 숫자(double)여야 합니다. 기본값은 1.0입니다.
크기 조정
값(선택 사항)을 입력하여 분포의 배율을 변경합니다. 분포에 크기 조정 값을 적용하여 분포를 늘리거나 줄일 수 있습니다.

값은 숫자(double)여야 합니다. 기본값은 1.0입니다.

기술 정보

이 섹션에는 구현 정보, 팁, 질문과 대답이 포함되어 있습니다.

구현 세부 정보

이 모듈은 오픈 소스 MATH.Net Numerics 라이브러리에서 제공되는 모든 분포를 지원합니다. 자세한 내용은 Math.Net.Numerics.Distribution 라이브러리에 대한 설명서를 참조하세요.

오른쪽 꼬리 및 2측 분포는 매개 변수가 있는 기본 배포판 버전이 아닌 별도의 배포로 표시됩니다. 현재 동작은 Excel과의 호환성을 유지하는 것입니다.

정의

이 모듈은 지정된 배포에 대해 다음 값의 계산을 지원합니다.

cdf 또는 누적 분포 함수

임의 변수가 특정 값 x보다 작은 값을 사용할 때 요동의 합계로 정의된 복합 이벤트의 확률을 반환합니다.

즉, "이 값보다 작거나 같은 샘플은 얼마나 일반적입니까?"라는 질문에 대답합니다.

이 함수는 연속 및 불연속 숫자 변수와 함께 사용할 수 있습니다.
InverseCdf 또는 역 누적 분포 함수

특정 누적 확률 값(cdf)과 연결된 값을 반환합니다.

즉, "cdf 함수가 누적 확률 y를 반환하는 x 값은 무엇인가요?"라는 질문에 대답합니다.
pdf 또는 확률 밀도 함수

임의 변수가 특정 값이 될 수 있는 상대 가능성을 설명합니다.

즉, "샘플이 정확히 이 값에서 얼마나 일반적입니까?"라는 질문에 대답합니다.

예상 입력

Name	Type	Description
데이터 세트	데이터 테이블	입력 데이터 세트

모듈 매개 변수

Name	범위	Type	기본값	Description
배포	모두	ProbabilityDistribution	StandardNormal	생성할 확률 분포의 종류를 선택합니다.
방법	모두	ProbabilityDistributionMethod	Cdf	선택한 확률 분포를 계산할 때 사용할 방법을 선택합니다. 누적 분포 함수(cdf), 역 누적 분포 함수(InverseCdf) 및 확률 밀도 함수 또는 질량 함수(pdf)의 옵션이 있습니다.
음 이항 분포 방법	모두	ProbabilityDistributionMethodForNegativeBinomial	Cdf	음 이항 분포를 선택하는 경우 분포를 평가하는 데 사용한 방법을 지정합니다.
성공 확률	[0.0;1.0]	Float	0.5	성공의 확률로 사용할 값을 입력합니다.
셰이프	모두	Float	1.0	분포의 셰이프를 수정하는 값을 입력합니다.
확장	>=0.0	Float	1.0	분포의 크기를 변경하는 값을 입력하여 크기를 늘리거나 줄입니다.
시행 횟수	>=1	정수	3	시행 횟수를 지정합니다.
하한	모두	Float	0.0	분포의 하한으로 사용할 숫자를 입력합니다.
상한	모두	Float	1.0	분포의 상한으로 사용할 숫자를 입력합니다.
위치	모두	Float	0.0	분포에서 0 요소의 위치를 입력합니다.
자유도 개수	모두	Float	1.0	자유도의 수를 지정합니다.
분자의 자유도입니다.	모두	Float	3.0	분자의 자유도 수를 지정합니다.
분모의 자유도입니다.	모두	Float	6.0	분모의 자유도 수를 지정합니다.
Lambda	>=0.0	Float	1.0	람다 매개 변수의 값을 지정합니다.
샘플 수	모두	정수	9	샘플 수를 지정합니다.
성공 수	모두	정수	24	성공의 수로 사용할 값을 입력합니다.
모집단 크기	모두	정수	52	모집단 크기를 지정합니다.
평균	모두	Float	0.0	예상 평균 값을 입력합니다.
표준 편차	>=0.0	Float	1.0	예상 표준 편차를 입력합니다.
열 집합	모두	ColumnSelection		확률 분포를 계산할 열을 선택합니다.
결과 모드	모두	OutputTo	ResultOnly	출력 데이터 집합에 결과를 저장하는 방법을 지정합니다. 새 열 추가, 기존 열 대체 또는 결과만 출력 옵션이 있습니다.

출력

Name	Type	Description
결과 데이터 집합	데이터 테이블	출력 데이터 세트

예외

오류 메시지의 전체 목록은 모듈 오류 코드를 참조하세요.

예외	설명
오류 0017	하나 이상의 지정된 열에 현재 모듈에서 지원되지 않는 유형이 있으면 예외가 발생합니다.

Studio(클래식) 모듈과 관련된 오류 목록은 Machine Learning 오류 코드를 참조하세요.

API 예외 목록은 MACHINE LEARNING REST API 오류 코드를 참조하세요.

추가 정보

통계 함수
전체 모듈 목록

다음을 통해 공유