Zelfstudie: Een kwantumgenerator voor willekeurige getallen implementeren in Q#

Artikel
13-01-2025

In deze zelfstudie leert u hoe u een basis kwantumprogramma schrijft waarin Q# gebruik wordt gemaakt van de aard van de kwantummechanica om een willekeurig getal te produceren.

In deze zelfstudie leert u het volgende:

Maak een Q# programma.
Bekijk de belangrijkste onderdelen van een Q# programma.
Definieer de logica van een probleem.
Combineer klassieke en kwantumbewerkingen om een probleem op te lossen.
Werken met qubits en superpositie om een kwantumgenerator van willekeurige getallen te maken.

Tip

Als u uw kwantumcomputingtraject wilt versnellen, bekijkt u Code met Azure Quantum, een unieke functie van de Azure Quantum-website. Hier kunt u ingebouwde Q# voorbeelden of uw eigen Q# programma's uitvoeren, nieuwe Q# code genereren vanuit uw prompts, uw code openen en uitvoeren in VS Code voor het web met één klik en Copilot vragen stellen over kwantumcomputing.

Vereisten

Het codevoorbeeld uitvoeren in Copilot in Azure Quantum:
- Een Microsoft-e-mailaccount (MSA).
Het codevoorbeeld ontwikkelen en uitvoeren in Visual Studio Code:
- Open de nieuwste versie van Visual Studio Code of VS Code op het web.
- De nieuwste versie van de Azure-extensieQuantum Development Kit. Zie De QDK-extensie instellenvoor installatiedetails.
- Als u Jupyter Notebooks wilt gebruiken, moet u ook Python, Jupyter-extensies en het nieuwste Python-pakket installeren. Hiervoor opent u een terminal en voert u de volgende opdracht uit:
  
  Bash
```
$ pip install --upgrade  qsharp
```

Het probleem definiëren

Klassieke computers produceren geen willekeurige getallen, maar eerder pseudorandom getallen. Een pseudorandom-getalgenerator genereert een deterministische reeks getallen op basis van een bepaalde initiële waarde, een seed genoemd. Voor een betere benadering van willekeurige waarden is deze seed vaak de huidige tijd van de CPU-klok.

Kwantumcomputers kunnen daarentegen echt willekeurige getallen genereren. Dit komt doordat de meting van een qubit in superpositie een probabilistisch proces is. Het resultaat van de meting is willekeurig en er is geen manier om het resultaat te voorspellen. Dit is het basisprincipe van kwantumgeneratoren voor willekeurige getallen.

Een qubit is een eenheid van kwantumgegevens die zich in superpositie kunnen bevindt. Wanneer gemeten, kan een qubit alleen de status 0 of de 1-status hebben. Voordat de meting wordt uitgevoerd, vertegenwoordigt de toestand van de qubit echter de waarschijnlijkheid van het lezen van een 0 of een 1 met een meting.

U begint met het nemen van een qubit in een basisstatus, bijvoorbeeld nul. De eerste stap van de generator voor willekeurige getallen is het gebruik van een Hadamard-bewerking om de qubit in een gelijke superpositie te plaatsen. De meting van deze toestand resulteert in een nul of een één, met een waarschijnlijkheid van 50% voor elk resultaat, een echt willekeurig bit.

Er is geen manier om te weten wat u krijgt na de meting van de qubit in superpositie en het resultaat is een andere waarde telkens wanneer de code wordt aangeroepen. Maar hoe kunt u dit gedrag gebruiken om grotere willekeurige getallen te genereren?

Stel dat u het proces vier keer herhaalt, waarna deze reeks binaire cijfers wordt gegenereerd:

$0, 1, 1, 0$

Als u deze bits samenvoegt of combineert in een bit-tekenreeks, kunt u een groter getal vormen. In dit voorbeeld is de bitreeks $0110$ gelijk aan zes in decimalen.

$0110_{b i n a r y} \equiv 6_{d e c i m a l}$

Als u dit proces meerdere keren herhaalt, kunt u meerdere bits combineren om een groot getal te vormen. Met deze methode kunt u een getal maken dat moet worden gebruikt als een veilig wachtwoord, omdat u er zeker van kunt zijn dat geen hacker de resultaten van de reeks metingen kan bepalen.

De logica definiëren voor de generator voor willekeurige getallen

Laten we eens een overzicht geven van de logica van een generator voor willekeurige getallen:

Definieer max het maximumaantal dat u wilt genereren.
Definieer het aantal willekeurige bits dat u moet genereren. Dit wordt gedaan door te berekenen hoeveel bits je nodig hebt om gehele getallen uit te drukken tot max.
Genereer een willekeurige binaire string met een lengte van nBits.
Als de bit-tekenreeks een getal vormt dat groter is dan max, gaat u terug naar stap 3.
Is dat niet het geval, dan is het proces voltooid. Retourneer het gegenereerde getal als een geheel getal.

Laten we bijvoorbeeld max instellen op 12. Dat wil gezegd: 12 is het grootste getal dat u als wachtwoord wilt gebruiken.

U hebt $⌊ l n (12) / l n (2) + 1 ⌋$ of 4 bits nodig om een getal tussen 0 en 12 weer te geven. We kunnen de ingebouwde functie BitSizeIgebruiken, die elk geheel getal accepteert en het aantal bits retourneert dat nodig is om deze weer te geven.

Stel dat u de bit-tekenreeks $1101_{b i n a r y}$ wilt genereren, wat gelijk is aan $13_{d e c i m a l}$ . Omdat 13 groter is dan 12, herhaalt u het proces.

Vervolgens genereert u de bit-tekenreeks $0110_{b i n a r y}$ , die gelijk is aan $6_{d e c i m a l}$ . Omdat 6 kleiner is dan 12, is het proces voltooid.

De kwantumgenerator voor willekeurige getallen retourneert nummer 6 als uw wachtwoord. Stel in de praktijk een groter getal in als het maximum, omdat lagere getallen eenvoudig te kraken zijn door alleen alle mogelijke wachtwoorden te proberen. Om de moeite van het raden of kraken van uw wachtwoord te vergroten, kunt u ASCII-code gebruiken om binair naar tekst te converteren en een wachtwoord te genereren met behulp van cijfers, symbolen en gemengde letters.

Een willekeurige bitgenerator schrijven

De eerste stap is het schrijven van een Q# bewerking waarmee een willekeurige bit wordt gegenereerd. Deze bewerking is een van de bouwstenen van de generator voor willekeurige getallen.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Bekijk nu nieuwe code.

U definieert de GenerateRandomBit bewerking, die geen invoer gebruikt en een waarde van het type Resultproduceert. Het Result type vertegenwoordigt het resultaat van een meting en kan twee mogelijke waarden hebben: Zero of One.
U wijst één qubit toe met het use trefwoord. Wanneer deze wordt toegewezen, heeft een qubit altijd de status |0〉.
U gebruikt de H bewerking om de qubit in een gelijke superpositie te plaatsen.
U gebruikt de bewerking om de M qubit te meten, de gemeten waarde (Zero of One) te retourneren.
U gebruikt de Reset bewerking om de qubit opnieuw in te stellen op de status |0〉.

Door de qubit in superpositie te plaatsen met de H bewerking en deze te meten met de M bewerking, is het resultaat telkens wanneer de code wordt aangeroepen een andere waarde.

Visualiseer de Q# code met de Bloch sphere

In de Blochbol vertegenwoordigt de noordpool de klassieke waarde 0 en de zuidpool de klassieke waarde 1. Elke superpositie kan worden weergegeven met een punt op de bol (aangeduid met een pijl). Hoe dichter het einde van de pijl bij een pool is, hoe groter de kans is dat de qubit bij meting uiteenvalt in de klassieke waarde die aan die pool is toegewezen. De qubitstatus die wordt vertegenwoordigd door de pijl in de volgende afbeelding, heeft bijvoorbeeld een hogere kans om de waarde 0 op te geven als u deze meet.

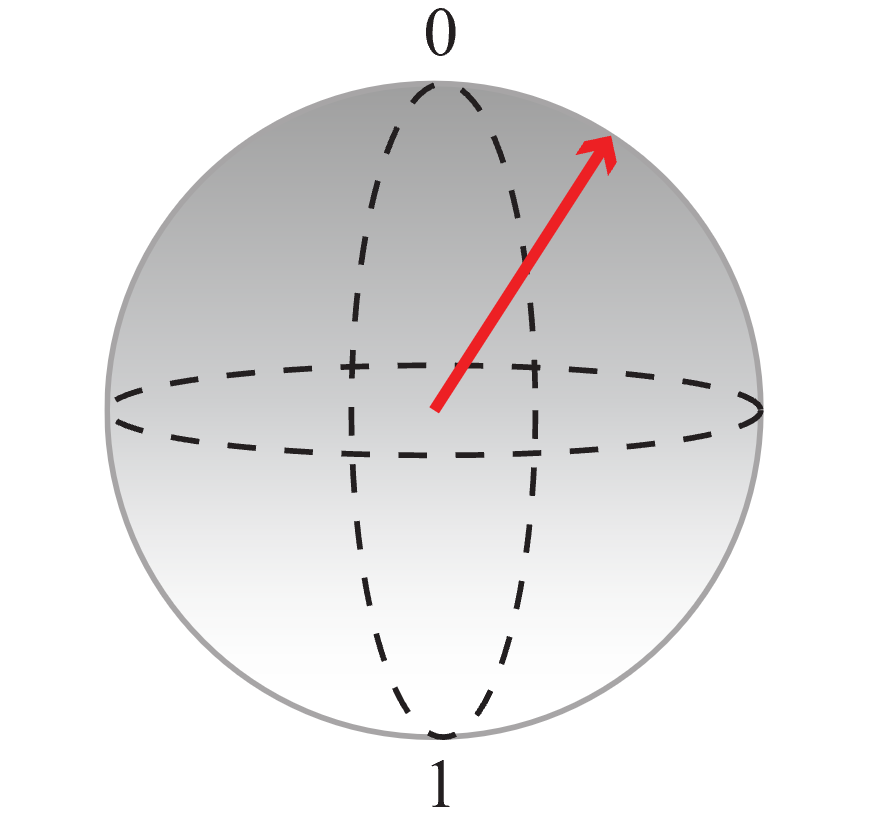
Een diagram met een qubitstatus met een hoge waarschijnlijkheid van het meten van nul.

U kunt deze weergave gebruiken om te visualiseren wat de code doet:

Begin eerst met een qubit die is geïnitialiseerd in de toestand |0〉 en pas een bewerking toe om een H gelijke superpositie te maken waarin de waarschijnlijkheden voor 0 en 1 hetzelfde zijn.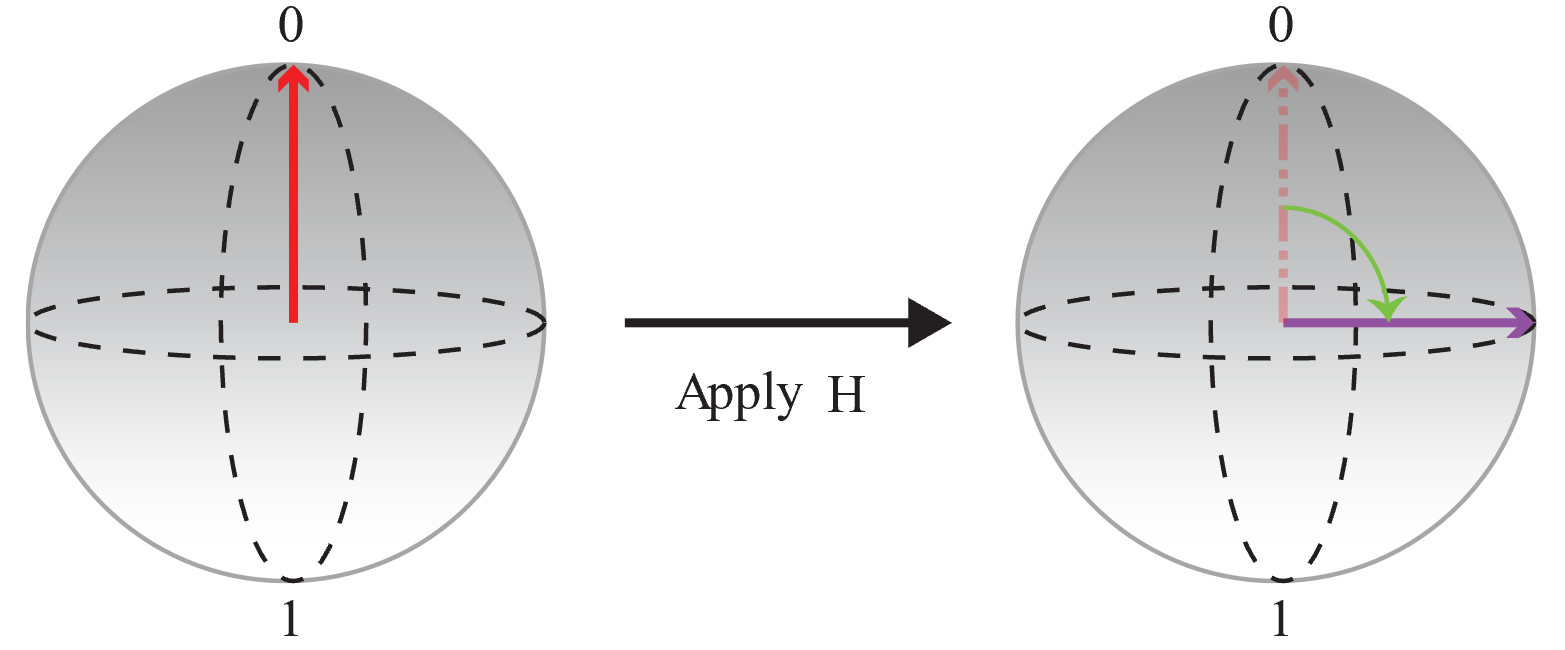
Meet vervolgens de qubit en sla de uitvoer op:

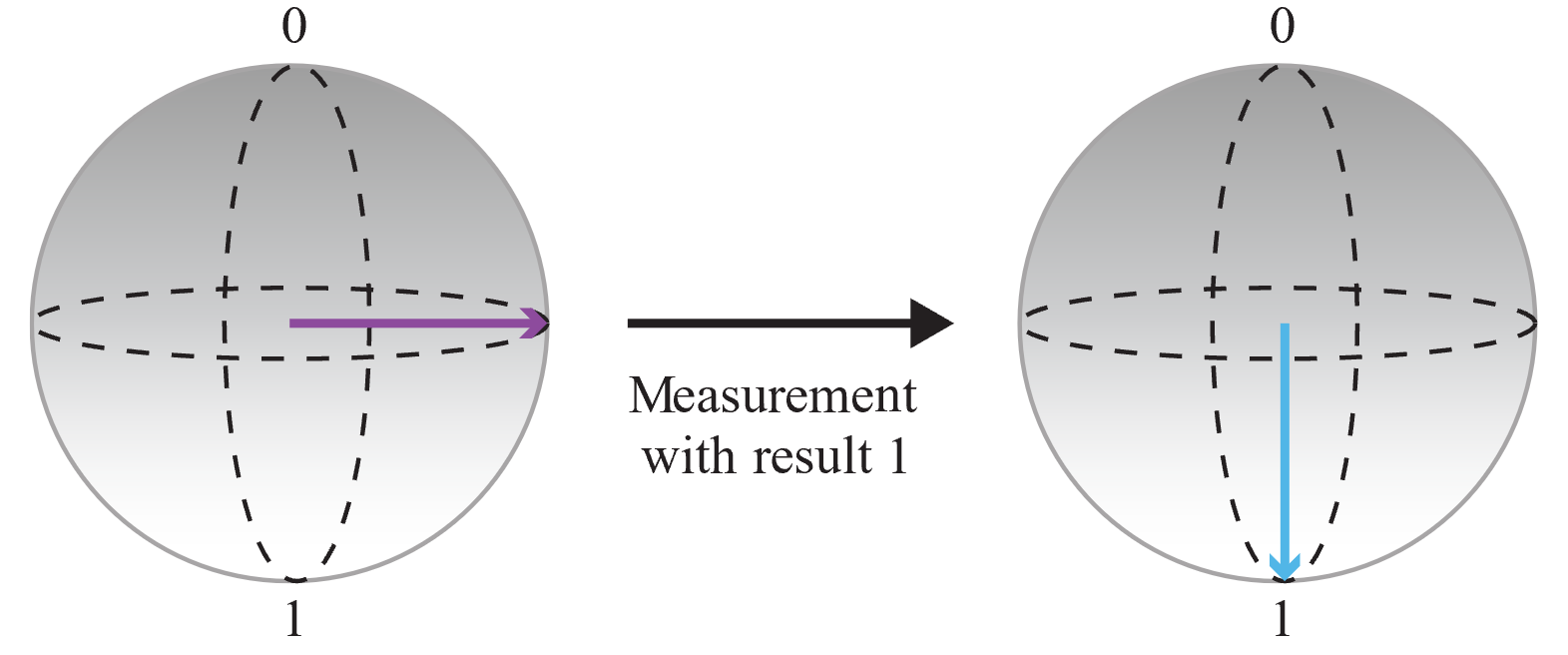
Omdat het resultaat van de meting willekeurig is en de waarschijnlijkheid van het meten van 0 en 1 hetzelfde is, hebt u een volledig willekeurige bit verkregen. U kunt deze bewerking meerdere keren aanroepen om gehele getallen te maken. Als u de bewerking bijvoorbeeld drie keer aanroept om drie willekeurige bits te verkrijgen, kunt u willekeurige 3-bits getallen maken (dat wil gezegd een willekeurig getal tussen 0 en 7).

Een volledige generator voor willekeurige getallen schrijven

Eerst moet u de vereiste naamruimten uit de Q# standaardbibliotheek importeren in het programma. De Q# compiler laadt veel algemene functies en bewerkingen automatisch, maar voor de volledige generator voor willekeurige getallen hebt u enkele extra functies en bewerkingen uit twee Q# naamruimten nodig: Microsoft.Quantum.Mathen Microsoft.Quantum.Convert.

Q#
```
import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;
```
Vervolgens definieert u de GenerateRandomNumberInRange bewerking. Met deze bewerking wordt herhaaldelijk de bewerking GenerateRandomBit aangeroepen om een bit-tekenreeks te maken.

Q#
```
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}
```
Laten we nog even de nieuwe code controleren.
- U moet berekenen hoeveel bits nodig zijn om getallen tot aan max uit te drukken. De BitSizeI functie van de Microsoft.Quantum.Math naamruimte converteert een geheel getal naar het aantal bits dat nodig is om deze weer te geven.
- De bewerking SampleRandomNumberInRange maakt gebruik van een for-lus om willekeurige getallen te genereren totdat er één wordt gegenereerd die gelijk is aan of kleiner is dan max. De for lus werkt precies hetzelfde als een for lus in andere programmeertalen.
- De variabele is een veranderlijke variabele bits . Een veranderlijke variabele kan tijdens de berekening worden gewijzigd. U kunt met de set-instructie de waarde van een veranderlijke variabele wijzigen.
- De ResultArrayAsInt functie converteert de bittekenreeks vanuit de standaardnaamruimte Microsoft.Quantum.Convert naar een positief geheel getal.
Ten slotte voegt u een toegangspunt toe aan het programma. Standaard zoekt de compiler naar een Main bewerking en begint daar met verwerken. Hiermee wordt de GenerateRandomNumberInRange bewerking aanroepen om een willekeurig getal te genereren tussen 0 en 100.

Q#
```
operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}
```
De let-instructie declareert variabelen die niet worden gewijzigd tijdens de berekening. Hier definieert u de maximumwaarde als 100.

Voor meer informatie over de Main-bewerking, zie Entry Points.
De volledige code voor de generator voor willekeurige getallen is als volgt:

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Het generatorprogramma voor willekeurige getallen uitvoeren

U kunt het programma uitvoeren in Copilot in Azure Quantum en in Visual Studio Code als zelfstandige Q# toepassing of met behulp van een Python-hostprogramma.

U kunt uw Q# code gratis testen met Copilot in Azure Quantum. U hebt alleen een Microsoft-e-mailaccount (MSA) nodig. Zie Azure Quantum verkennen voor meer informatie over Copilot in Azure Quantum.

Open Copilot in Azure Quantum in uw browser.

Kopieer en plak de volgende code in de code-editor.

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Selecteer het aantal schermafbeeldingen dat moet worden uitgevoerd en selecteer Uitvoeren.
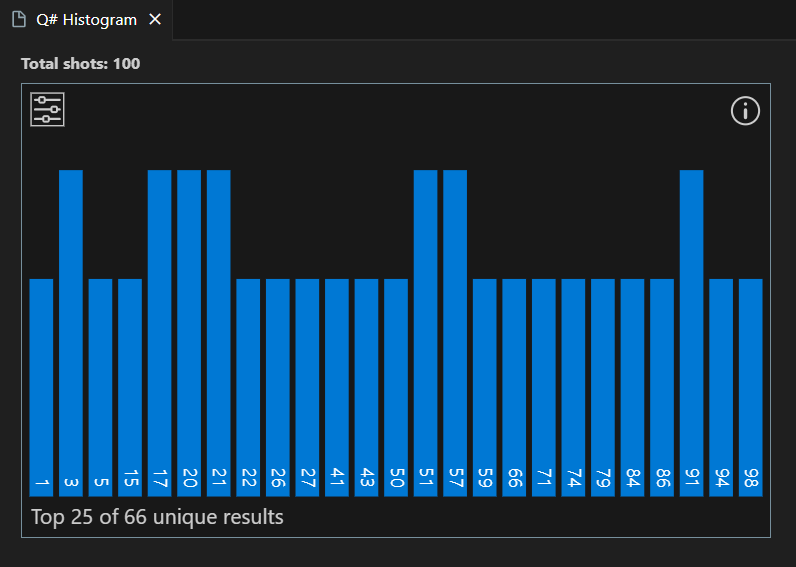
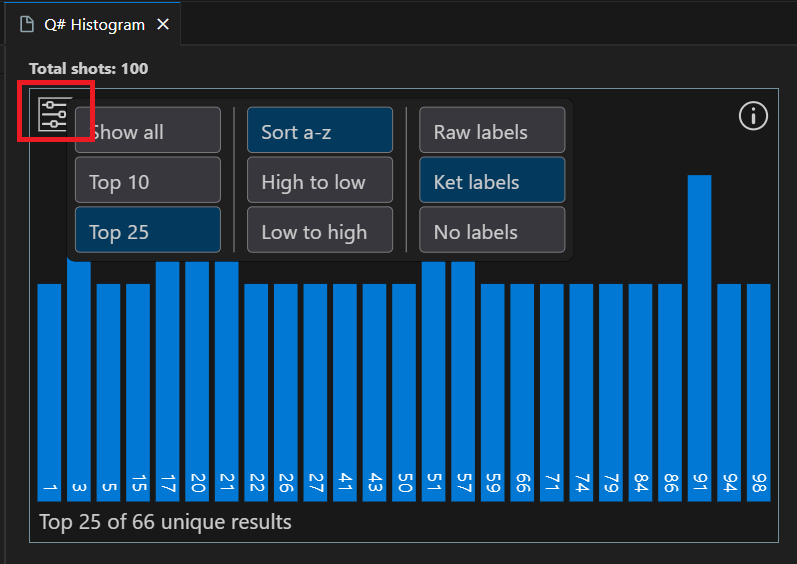
De resultaten worden weergegeven in het histogram en in de resultatenvelden .
Selecteer Code uitleggen om Copilot te vragen om de code aan u uit te leggen.

Tip

Vanuit Copilot in Azure Quantum kunt u uw programma openen in VS Code for the Web door in de rechterhoek van de code-editor de knop VS Code-logo te selecteren.

Open Visual Studio Code en selecteer Bestand > nieuw tekstbestand om een nieuw bestand te maken.
Sla het bestand op als RandomNumberGenerator.qs. Dit bestand bevat de Q# code voor uw programma.

Kopieer de volgende code in het RandomNumberGenerator.qs bestand.


import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Voordat u het programma uitvoert, moet u het target profiel instellen op Unrestricted. Selecteer View -> Command Palette, zoek naar QIR, selecteer Q#: Stel het Azure Quantum QIR-profiel targetin en selecteer Q#vervolgens : onbeperkt.
Als u uw programma wilt uitvoeren, selecteert u Uitvoeren Bestand in de vervolgkeuzelijst van het afspelen-icoon rechtsboven, selecteer Uitvoeren uit de lijst van opdrachten boven Main(), of druk op Ctrl+F5. Het programma voert de Main() bewerking uit op de standaardsimulator.
Uw uitvoer wordt weergegeven in de console voor foutopsporing.
Voer het programma opnieuw uit om een ander resultaat te zien.

Notitie

Als het target profiel niet is ingesteld op Onbeperkt, krijgt u een foutmelding wanneer u het programma uitvoert.

Het frequentie histogram tekenen

Laten we de distributie visualiseren van resultaten die zijn verkregen door het uitvoeren van het kwantumprogramma meerdere keren. Het frequentie histogram helpt bij het visualiseren van de waarschijnlijkheidsverdeling van deze resultaten.

Selecteer Weergave -> Opdrachtpalet en typ 'histogram', waarmee de optie Q#: Bestand uitvoeren en histogram weergeven verschijnt. U kunt ook Histogram selecteren in de lijst met opdrachten die voorafgaan aan Main(). Selecteer deze optie om het Q# histogramvenster te openen.
Voer een aantal uitvoeringen in om het programma uit te voeren, bijvoorbeeld 100 uitvoeringen, en druk op Enter. Het histogram wordt weergegeven in het Q# histogramvenster.
Elke balk in het histogram komt overeen met een mogelijk resultaat en de hoogte geeft het aantal keren aan dat het resultaat wordt waargenomen. Het aantal verschillende resultaten kan verschillen telkens wanneer u het histogram uitvoert.

Tip

U kunt het histogram inzoomen met behulp van het muiswiel of een trackpadbeweging. Wanneer u inzoomt, kunt u de grafiek pannen door tijdens het schuiven op Alt te drukken.
Selecteer een balk om het percentage van dat resultaat weer te geven.
Selecteer het pictogram met instellingen linksboven om opties weer te geven. U kunt top 10 resultaten, top 25 resultaten of alle resultaten weergeven. U kunt de resultaten ook sorteren van hoog naar laag of van laag naar hoog.

Selecteer in VS Code Weergeven Command palette en selecteer Maken: Nieuw Jupyter Notebook.
Importeer in de eerste cel het qsharp pakket in uw Python-code:

Python
```
import qsharp
```

Voeg de Q# code toe voor het kwantumgeneratorprogramma voor willekeurige getallen. Hiervoor gebruikt u de %%qsharp magic-opdracht. Houd er rekening mee dat de %%qsharp opdracht de notebookcel wijzigt van type Python in type Q#. Kopieer deze code naar de tweede cel.

%%qsharp

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Voer ten slotte de code uit. U kunt dezelfde simulatie een aantal keren afzonderlijk uitvoeren. Elke onafhankelijke simulatie wordt een 'shot' genoemd. Laten we bijvoorbeeld de simulatie 100 keer uitvoeren.

Python
```
results = qsharp.run("Main()", shots=100)
print(results)
```

Notitie

Dit codefragment wordt momenteel niet uitgevoerd op beschikbare Azure Quantum-hardware targets, omdat het aanroepbare ResultArrayAsInt een QPU met een volledig rekenprofiel vereist.

Bekijk andere Q# handleidingen:

Kwantumverstrengeling laat zien hoe u een Q# programma schrijft dat qubits bewerkt en meet en de effecten van superpositie en verstrengeling demonstreert.
Het zoekalgoritmen van Grover laten zien hoe u een Q# programma schrijft dat gebruikmaakt van het zoekalgoritmen van Grover.
Met Quantum Fourier-transformaties wordt uitgelegd hoe u een Q# programma schrijft waarmee specifieke qubits rechtstreeks worden aangepakt.
De Quantum Katas zijn zelfstudies in eigen tempo en programmeeroefeningen die zijn gericht op het leren van de elementen van kwantumcomputing en Q# programmeren op hetzelfde moment.

Aanvullende resources

Documentatie

Zelfstudie: Kwantumverstrengeling met Q# - Azure Quantum

In deze zelfstudie schrijf je een kwantumprogramma in Q# dat de superpositie en verstrengeling van qubits demonstreert.
Zelfstudie: Quantum Fourier-transformatie in Q\ # - Azure Quantum

In deze zelfstudie leert u hoe u een kwantumprogramma schrijft en simuleert dat op het niveau van de afzonderlijke qubit werkt.
Quickstart: Een Q# programma maken - Azure Quantum

In dit artikel wordt uitgelegd hoe u uw eerste Q# programma maakt met behulp van de Quantum Development Kit en Visual Studio Code.
Zelfstudie: Het algoritme van Grover implementeren in Q# - Azure Quantum

In deze zelfstudie bouwt u een Q# project dat het zoekalgoritme van Grover demonstreert, een van de canonieke kwantumalgoritmen.
Inleiding tot de Kwantumprogrammeertaal Q# - Azure Quantum

In dit artikel wordt een programmeertaal geïntroduceerd Q#voor het ontwikkelen en uitvoeren van kwantumalgoritmen en de structuur van een Q# programma.
Projecten en aangepaste bibliotheken ontwikkelen en beheren Q# - Azure Quantum

Meer informatie over het definiëren van een Q# project dat gebruikmaakt van meerdere bronbestanden en het gebruik van uw projecten als herbruikbare aangepaste bibliotheken.
Q#-functies in Visual Studio Code - Azure Quantum

Meer informatie over de functies die zijn opgenomen in de Azure Quantum Development Kit-extensie voor VS Code.
Fouten opsporen en kwantumprogramma's testen in Azure Quantum - Azure Quantum

Leer hoe u eenheidstests, feiten en asserties en dumpfuncties gebruikt om kwantumprogramma's te testen en fouten op te sporen.

Training

Module

Uw eerste Q#-programma maken met behulp van de Azure Quantum Development Kit - Training

Aan de slag met Q#-programmering door een kwantumgenerator voor willekeurige getallen te maken.

AI Skills Fest

Delen via

Zelfstudie: Een kwantumgenerator voor willekeurige getallen implementeren in Q#

Vereisten

Het probleem definiëren

De logica definiëren voor de generator voor willekeurige getallen

Een willekeurige bitgenerator schrijven

Visualiseer de Q# code met de Bloch sphere

Een volledige generator voor willekeurige getallen schrijven

Het generatorprogramma voor willekeurige getallen uitvoeren

Het frequentie histogram tekenen

Feedback

Aanvullende resources

AI Skills Fest

Delen via

Zelfstudie: Een kwantumgenerator voor willekeurige getallen implementeren in Q#

Vereisten

Het probleem definiëren

De logica definiëren voor de generator voor willekeurige getallen

Een willekeurige bitgenerator schrijven

Visualiseer de Q# code met de Bloch sphere

Een volledige generator voor willekeurige getallen schrijven

Het generatorprogramma voor willekeurige getallen uitvoeren

Gerelateerde inhoud

Feedback

Aanvullende resources