Handleiding voor net#-taal voor neurale netwerkspecificatie voor Machine Learning Studio (klassiek)
VAN TOEPASSING OP:  Machine Learning Studio (klassiek)
Machine Learning Studio (klassiek)  Azure Machine Learning
Azure Machine Learning
Belangrijk
De ondersteuning voor Azure Machine Learning-studio (klassiek) eindigt op 31 augustus 2024. U wordt aangeraden om vóór die datum over te stappen naar Azure Machine Learning.
Vanaf 1 december 2021 kunt u geen nieuwe resources voor Azure Machine Learning-studio (klassiek) meer maken. Tot en met 31 augustus 2024 kunt u de bestaande resources van Azure Machine Learning-studio (klassiek) blijven gebruiken.
- Zie informatie over het verplaatsen van machine learning-projecten van ML Studio (klassiek) naar Azure Machine Learning.
- Meer informatie over Azure Machine Learning
De documentatie van ML-studio (klassiek) wordt buiten gebruik gesteld en wordt in de toekomst mogelijk niet meer bijgewerkt.
Net# is een taal die is ontwikkeld door Microsoft die wordt gebruikt om complexe neurale netwerkarchitecturen zoals diepe neurale netwerken of samenvoegingen van willekeurige dimensies te definiëren. U kunt complexe structuren gebruiken om het leren over gegevens zoals afbeeldingen, video of audio te verbeteren.
U kunt een Net#-architectuurspecificatie gebruiken in alle neurale netwerkmodules in Machine Learning Studio (klassiek):
In dit artikel worden de basisconcepten en syntaxis beschreven die nodig zijn om een aangepast neuraal netwerk te ontwikkelen met Net#:
- Vereisten voor neurale netwerken en het definiëren van de primaire onderdelen
- De syntaxis en trefwoorden van de Net#-specificatietaal
- Voorbeelden van aangepaste neurale netwerken die zijn gemaakt met net#
Basisbeginselen van neurale netwerken
Een neurale netwerkstructuur bestaat uit knooppunten die zijn ingedeeld in lagen en gewogen verbindingen (of randen) tussen de knooppunten. De verbindingen zijn richtingen en elke verbinding heeft een bronknooppunt en een doelknooppunt.
Elke trainbare laag (een verborgen of uitvoerlaag) heeft een of meer verbindingsbundels. Een verbindingsbundel bestaat uit een bronlaag en een specificatie van de verbindingen van die bronlaag. Alle verbindingen in een bepaalde bundelsharebron- en doellagen. In Net# wordt een verbindingsbundel beschouwd als behorend tot de doellaag van de bundel.
Net# ondersteunt verschillende soorten verbindingsbundels, waarmee u de manier kunt aanpassen waarop invoer wordt toegewezen aan verborgen lagen en worden toegewezen aan de uitvoer.
De standaardbundel of standaardbundel is een volledige bundel, waarin elk knooppunt in de bronlaag is verbonden met elk knooppunt in de doellaag.
Daarnaast ondersteunt Net# de volgende vier soorten geavanceerde verbindingsbundels:
Gefilterde bundels. U kunt een predicaat definiëren met behulp van de locaties van het bronlaagknooppunt en het doellaagknooppunt. Knooppunten worden verbonden wanneer het predicaat Waar is.
Convolutionele bundels. U kunt kleine buurten van knooppunten definiëren in de bronlaag. Elk knooppunt in de doellaag is verbonden met één buurt van knooppunten in de bronlaag.
Bundels en antwoordnormalisatiebundels groeperen. Deze zijn vergelijkbaar met convolutionele bundels omdat de gebruiker kleine buurten van knooppunten in de bronlaag definieert. Het verschil is dat de gewichten van de randen in deze bundels niet kunnen worden getraind. In plaats daarvan wordt een vooraf gedefinieerde functie toegepast op de waarden van het bronknooppunt om de waarde van het doelknooppunt te bepalen.
Ondersteunde aanpassingen
De architectuur van neurale netwerkmodellen die u maakt in Machine Learning Studio (klassiek) kan uitgebreid worden aangepast met Behulp van Net#. U kunt:
- Maak verborgen lagen en beheer het aantal knooppunten in elke laag.
- Geef op hoe lagen met elkaar moeten worden verbonden.
- Definieer speciale verbindingsstructuren, zoals convolutions en bundels voor het delen van gewichten.
- Geef verschillende activeringsfuncties op.
Zie Structuurspecificatie voor meer informatie over de syntaxis van de specificatietaal.
Zie Voorbeelden voor voorbeelden van het definiëren van neurale netwerken voor enkele algemene machine learning-taken, van simplex tot complex.
Algemene vereisten
- Er moet precies één uitvoerlaag, ten minste één invoerlaag en nul of meer verborgen lagen zijn.
- Elke laag heeft een vast aantal knooppunten, conceptueel gerangschikt in een rechthoekige matrix van willekeurige dimensies.
- Invoerlagen hebben geen gekoppelde getrainde parameters en vertegenwoordigen het punt waarop exemplaargegevens het netwerk binnenkomen.
- Trainbare lagen (de verborgen en uitvoerlagen) hebben getrainde parameters gekoppeld, ook wel gewichten en vooroordelen genoemd.
- De bron- en doelknooppunten moeten zich in afzonderlijke lagen bevinden.
- Verbindingen moeten acyclisch zijn; met andere woorden, er kan geen keten van verbindingen zijn die terugleiden naar het eerste bronknooppunt.
- De uitvoerlaag kan geen bronlaag van een verbindingsbundel zijn.
Structuurspecificaties
Een specificatie van een neurale netwerkstructuur bestaat uit drie secties: de constante declaratie, de laagdeclaratie, de verbindingsdeclaratie. Er is ook een optionele sectie voor sharedeclaratie . De secties kunnen in elke volgorde worden opgegeven.
Constante declaratie
Een constante declaratie is optioneel. Het biedt een middel om waarden te definiëren die elders in de definitie van het neurale netwerk worden gebruikt. De declaratie-instructie bestaat uit een id gevolgd door een gelijkteken en een waardeexpressie.
Met de volgende instructie wordt bijvoorbeeld een constante xgedefinieerd:
Const X = 28;
Als u twee of meer constanten tegelijk wilt definiëren, plaatst u de id-namen en -waarden tussen accolades en scheidt u deze met puntkomma's. Voorbeeld:
Const { X = 28; Y = 4; }
De rechterkant van elke toewijzingsexpressie kan een geheel getal, een reëel getal, een Booleaanse waarde (Waar of Onwaar) of een wiskundige expressie zijn. Voorbeeld:
Const { X = 17 * 2; Y = true; }
Laagdeclaratie
De laagdeclaratie is vereist. Hiermee definieert u de grootte en bron van de laag, inclusief de bijbehorende verbindingsbundels en -kenmerken. De declaratie-instructie begint met de naam van de laag (invoer, verborgen of uitvoer), gevolgd door de dimensies van de laag (een tuple met positieve gehele getallen). Voorbeeld:
input Data auto;
hidden Hidden[5,20] from Data all;
output Result[2] from Hidden all;
- Het product van de dimensies is het aantal knooppunten in de laag. In dit voorbeeld zijn er twee dimensies [5.20], wat betekent dat er 100 knooppunten in de laag zijn.
- De lagen kunnen in elke volgorde worden gedeclareerd, met één uitzondering: als er meer dan één invoerlaag is gedefinieerd, moet de volgorde waarin ze worden gedeclareerd overeenkomen met de volgorde van functies in de invoergegevens.
Als u wilt opgeven dat het aantal knooppunten in een laag automatisch wordt bepaald, gebruikt u het auto trefwoord. Het auto trefwoord heeft verschillende effecten, afhankelijk van de laag:
- In een declaratie van een invoerlaag is het aantal knooppunten het aantal functies in de invoergegevens.
- In een verborgen laagdeclaratie is het aantal knooppunten het aantal knooppunten dat is opgegeven door de parameterwaarde voor het aantal verborgen knooppunten.
- In een uitvoerlaagdeclaratie is het aantal knooppunten 2 voor classificatie van twee klassen, 1 voor regressie en gelijk aan het aantal uitvoerknooppunten voor classificatie met meerdere klassen.
Met de volgende netwerkdefinitie kan bijvoorbeeld automatisch de grootte van alle lagen worden bepaald:
input Data auto;
hidden Hidden auto from Data all;
output Result auto from Hidden all;
Een laagdeclaratie voor een trainbare laag (de verborgen of uitvoerlagen) kan eventueel de uitvoerfunctie (ook wel een activeringsfunctie genoemd) bevatten, die standaard sigmoid voor classificatiemodellen en lineair is voor regressiemodellen. Zelfs als u de standaardwaarde gebruikt, kunt u de activeringsfunctie expliciet aangeven, indien gewenst voor duidelijkheid.
De volgende uitvoerfuncties worden ondersteund:
- Sigmoid
- lineair
- softmax
- rlinear
- vierkant
- Sqrt
- srlinear
- ABS
- Tanh
- brlinear
De volgende declaratie maakt bijvoorbeeld gebruik van de softmax-functie :
output Result [100] softmax from Hidden all;
Verbindingsdeclaratie
Direct nadat u de trainbare laag hebt gedefinieerd, moet u verbindingen declareren tussen de lagen die u hebt gedefinieerd. De declaratie van de verbindingsbundel begint met het trefwoord from, gevolgd door de naam van de bronlaag van de bundel en het soort verbindingsbundel dat moet worden gemaakt.
Op dit moment worden vijf soorten verbindingsbundels ondersteund:
- Volledige bundels, aangegeven met het trefwoord
all - Gefilterde bundels, aangegeven met het trefwoord
where, gevolgd door een predicaatexpressie - Convolutionele bundels, aangegeven met het trefwoord
convolve, gevolgd door de convolutionele kenmerken - Bundels groeperen , aangegeven met de trefwoorden max. pool of gemiddelde pool
- Antwoordnormalisatiebundels, aangegeven door de antwoordnorm voor trefwoorden
Volledige bundels
Een volledige verbindingsbundel bevat een verbinding van elk knooppunt in de bronlaag naar elk knooppunt in de doellaag. Dit is het standaardnetwerkverbindingstype.
Gefilterde bundels
Een gefilterde verbindingsbundelspecificatie bevat een predicaat, uitgedrukt syntactisch, net als een C#-lambda-expressie. In het volgende voorbeeld worden twee gefilterde bundels gedefinieerd:
input Pixels [10, 20];
hidden ByRow[10, 12] from Pixels where (s,d) => s[0] == d[0];
hidden ByCol[5, 20] from Pixels where (s,d) => abs(s[1] - d[1]) <= 1;
In het predicaat voor
ByRow,sis een parameter die een index vertegenwoordigt in de rechthoekige matrix van knooppunten van de invoerlaag,Pixelsendis een parameter die een index vertegenwoordigt in de matrix van knooppunten van de verborgen laag,ByRow. Het type van beidesendis een tuple van gehele getallen van lengte twee. Conceptueelsgezien bereiken over alle paren gehele getallen met0 <= s[0] < 10en , en0 <= s[1] < 20dbereiken over alle paren gehele getallen, met0 <= d[0] < 10en0 <= d[1] < 12.Aan de rechterkant van de predicaatexpressie is er een voorwaarde. In dit voorbeeld is er voor elke waarde van
sendzodanig dat de voorwaarde Waar is, een rand van het knooppunt van de bronlaag naar het doellaagknooppunt. Deze filterexpressie geeft dus aan dat de bundel een verbinding bevat van het knooppunt dat is gedefinieerd metshet knooppunt dat isdgedefinieerd in alle gevallen waarin s[0] gelijk is aan d[0].
U kunt eventueel een set gewichten opgeven voor een gefilterde bundel. De waarde voor het kenmerk Gewichten moet een tuple zijn van drijvendekommawaarden met een lengte die overeenkomt met het aantal verbindingen dat door de bundel is gedefinieerd. Standaard worden gewichten willekeurig gegenereerd.
Gewichtswaarden worden gegroepeerd op de doelknooppuntindex. Als het eerste doelknooppunt is verbonden met K-bronknooppunten, zijn de eerste K elementen van de tuple Gewichten de gewichten voor het eerste doelknooppunt, in de volgorde van de bronindex. Hetzelfde geldt voor de resterende doelknooppunten.
Het is mogelijk om gewichten rechtstreeks als constante waarden op te geven. Als u bijvoorbeeld eerder de gewichten hebt geleerd, kunt u deze opgeven als constanten met behulp van deze syntaxis:
const Weights_1 = [0.0188045055, 0.130500451, ...]
Convolutionele bundels
Wanneer de trainingsgegevens een homogene structuur hebben, worden convolutionele verbindingen vaak gebruikt om algemene functies van de gegevens te leren. In beeld-, audio- of videogegevens kan ruimtelijke of tijdelijke dimensionaliteit bijvoorbeeld redelijk uniform zijn.
Convolutionele bundels maken gebruik van rechthoekige kernels die door de dimensies worden geschoven. In wezen definieert elke kernel een set gewichten die in lokale buurten worden toegepast, ook wel kerneltoepassingen genoemd. Elke kerneltoepassing komt overeen met een knooppunt in de bronlaag, dat het centrale knooppunt wordt genoemd. De gewichten van een kernel worden gedeeld tussen veel verbindingen. In een convolutionele bundel is elke kernel rechthoekig en hebben alle kerneltoepassingen dezelfde grootte.
Convolutionele bundels ondersteunen de volgende kenmerken:
InputShape definieert de dimensionaliteit van de bronlaag voor de doeleinden van deze convolutionele bundel. De waarde moet een tuple van positieve gehele getallen zijn. Het product van de gehele getallen moet gelijk zijn aan het aantal knooppunten in de bronlaag, maar anders hoeft het niet overeen te komen met de dimensionaliteit die voor de bronlaag is gedeclareerd. De lengte van deze tuple wordt de ariteitswaarde voor de convolutionele bundel. Meestal verwijst arity naar het aantal argumenten of operanden dat een functie kan aannemen.
Als u de vorm en locaties van de kernels wilt definiëren, gebruikt u de kenmerken KernelShape, Stride, Padding, LowerPad en UpperPad:
KernelVorm: (vereist) Definieert de dimensionaliteit van elke kernel voor de convolutionele bundel. De waarde moet een tuple van positieve gehele getallen zijn met een lengte die gelijk is aan de ariteit van de bundel. Elk onderdeel van deze tuple mag niet groter zijn dan het bijbehorende onderdeel van InputShape.
Stride: (optioneel) Definieert de schuifstapgrootten van de convolutie (één stapgrootte voor elke dimensie), de afstand tussen de centrale knooppunten. De waarde moet een tupel van positieve gehele getallen zijn met een lengte die de ariteit van de bundel is. Elk onderdeel van deze tuple mag niet groter zijn dan het bijbehorende onderdeel van KernelShape. De standaardwaarde is een tuple met alle onderdelen die gelijk zijn aan één.
Delen: (optioneel) Definieert het gewicht delen voor elke dimensie van de convolution. De waarde kan één Booleaanse waarde of een tuple van Booleaanse waarden zijn met een lengte die de ariteit van de bundel is. Eén Booleaanse waarde wordt uitgebreid tot een tuple van de juiste lengte met alle onderdelen die gelijk zijn aan de opgegeven waarde. De standaardwaarde is een tuple die bestaat uit alle true-waarden.
MapCount: (optioneel) Definieert het aantal functietoewijzingen voor de convolutionele bundel. De waarde kan één positief geheel getal of een tuple van positieve gehele getallen zijn met een lengte die de ariteit van de bundel is. Eén geheel getal wordt uitgebreid tot een tuple van de juiste lengte met de eerste onderdelen die gelijk zijn aan de opgegeven waarde en alle resterende onderdelen gelijk aan één. De standaardwaarde is één. Het totale aantal functiekaarten is het product van de onderdelen van de tuple. De factoring van dit totale aantal voor de onderdelen bepaalt hoe de waarden van de functietoewijzing worden gegroepeerd in de doelknooppunten.
Gewichten: (optioneel) Definieert de initiële gewichten voor de bundel. De waarde moet een tuple zijn van drijvendekommawaarden met een lengte die het aantal kernels maalt het aantal gewichten per kernel, zoals verderop in dit artikel is gedefinieerd. De standaardgewichten worden willekeurig gegenereerd.
Er zijn twee sets eigenschappen waarmee de opvulling wordt beheerd. De eigenschappen sluiten elkaar wederzijds uit:
Opvulling: (optioneel) Bepaalt of de invoer moet worden opgevuld met behulp van een standaardopvullingsschema. De waarde kan één Booleaanse waarde zijn of een tuple van Booleaanse waarden met een lengte die de ariteit van de bundel is.
Eén Booleaanse waarde wordt uitgebreid tot een tuple van de juiste lengte met alle onderdelen die gelijk zijn aan de opgegeven waarde.
Als de waarde voor een dimensie Waar is, wordt de bron logisch opgevuld in die dimensie met cellen met nulwaarden ter ondersteuning van extra kerneltoepassingen, zodat de centrale knooppunten van de eerste en laatste kernels in die dimensie de eerste en laatste knooppunten in die dimensie zijn in die dimensie in de bronlaag. Het aantal 'dummy'-knooppunten in elke dimensie wordt dus automatisch bepaald, zodat de kernels exact
(InputShape[d] - 1) / Stride[d] + 1in de opgevulde bronlaag passen.Als de waarde voor een dimensie Onwaar is, worden de kernels gedefinieerd, zodat het aantal knooppunten aan elke zijde dat wordt gelaten, hetzelfde is (tot een verschil van 1). De standaardwaarde van dit kenmerk is een tuple met alle onderdelen die gelijk zijn aan False.
UpperPad en LowerPad: (optioneel) Geef meer controle over de hoeveelheid opvulling die moet worden gebruikt. Belangrijk: Deze kenmerken kunnen worden gedefinieerd als en alleen als de bovenstaande eigenschap Opvulling niet is gedefinieerd. De waarden moeten tuples met gehele getallen zijn met lengten die de ariteit van de bundel zijn. Wanneer deze kenmerken zijn opgegeven, worden 'dummy'-knooppunten toegevoegd aan de onderste en bovenste uiteinden van elke dimensie van de invoerlaag. Het aantal knooppunten dat aan de onderste en bovenste uiteinden in elke dimensie wordt toegevoegd, wordt bepaald door respectievelijk LowerPad[i] en UpperPad[i] .
Om ervoor te zorgen dat kernels alleen overeenkomen met 'echte' knooppunten en niet met 'dummy'-knooppunten, moet aan de volgende voorwaarden worden voldaan:
Elk onderdeel van LowerPad moet strikt kleiner zijn dan
KernelShape[d]/2.Elk onderdeel van UpperPad mag niet groter zijn dan
KernelShape[d]/2.De standaardwaarde van deze kenmerken is een tuple met alle onderdelen die gelijk zijn aan 0.
De instelling Padding = true staat zoveel opvulling toe als nodig is om het "midden" van de kernel binnen de "echte" invoer te houden. Hierdoor wordt de wiskunde enigszins gewijzigd voor het berekenen van de uitvoergrootte. Over het algemeen wordt de uitvoergrootte D berekend als
D = (I - K) / S + 1, waarIde invoergrootte is,Kis de kernelgrootte,Sde stride en/is de gehele verdeling (rond naar nul). Als u UpperPad = [1, 1] instelt, is de invoergrootteIeffectief 29 en dusD = (29 - 5) / 2 + 1 = 13. Echter, als padding = waar, inIwezen wordt opgestoten doorK - 1; vandaarD = ((28 + 4) - 5) / 2 + 1 = 27 / 2 + 1 = 13 + 1 = 14. Door waarden op te geven voor UpperPad en LowerPad krijgt u veel meer controle over de opvulling dan als u alleen Padding = true instelt.
Zie de volgende artikelen voor meer informatie over convolutionele netwerken en hun toepassingen:
- http://d2l.ai/chapter_convolutional-neural-networks/lenet.html
- https://research.microsoft.com/pubs/68920/icdar03.pdf
Poolbundels
Een poolbundel past geometrie toe die vergelijkbaar is met convolutionele connectiviteit, maar maakt gebruik van vooraf gedefinieerde functies voor bronknooppuntwaarden om de doelknooppuntwaarde af te leiden. Daarom hebben poolbundels geen trainbare status (gewichten of vooroordelen). Poolbundels ondersteunen alle convolutionele kenmerken, behalve Delen, MapCount en Weights.
Normaal gesproken overlappen de kernels die worden samengevat door aangrenzende pooleenheden niet. Als Stride[d] gelijk is aan KernelShape[d] in elke dimensie, is de verkregen laag de traditionele lokale poollaag, die meestal wordt gebruikt in convolutionele neurale netwerken. Elk doelknooppunt berekent het maximum of het gemiddelde van de activiteiten van de kernel in de bronlaag.
In het volgende voorbeeld ziet u een poolbundel:
hidden P1 [5, 12, 12]
from C1 max pool {
InputShape = [ 5, 24, 24];
KernelShape = [ 1, 2, 2];
Stride = [ 1, 2, 2];
}
- De arity van de bundel is 3: dat wil gezegd, de lengte van de tuples
InputShape,KernelShapeenStride. - Het aantal knooppunten in de bronlaag is
5 * 24 * 24 = 2880. - Dit is een traditionele lokale poollaag omdat KernelShape en Stride gelijk zijn.
- Het aantal knooppunten in de doellaag is
5 * 12 * 12 = 1440.
Zie de volgende artikelen voor meer informatie over poollagen:
- https://www.cs.toronto.edu/~hinton/absps/imagenet.pdf (Sectie 3.4)
- https://cs.nyu.edu/~koray/publis/lecun-iscas-10.pdf
- https://cs.nyu.edu/~koray/publis/jarrett-iccv-09.pdf
Reactienormalisatiebundels
Responsnormalisatie is een lokaal normalisatieschema dat voor het eerst is geïntroduceerd door Microsoft Hinton, et al, in de paper ImageNet Classification met Deep Convolutional Neural Networks.
Reactienormalisatie wordt gebruikt om generalisatie in neurale netwerken te helpen. Wanneer één neuron wordt geactiveerd op een zeer hoog activeringsniveau, onderdrukt een lokale responsnormalisatielaag het activeringsniveau van de omringende neuronen. Dit wordt gedaan met behulp van drie parameters (α, βen k) en een convolutionele structuur (of buurtvorm). Elke neuron in de doellaag y komt overeen met een neuron x in de bronlaag. Het activeringsniveau van y wordt gegeven door de volgende formule, waarbij f het activeringsniveau van een neuron is, en Nx is de kernel (of de set die de neuronen in de buurt van x bevat), zoals gedefinieerd door de volgende convolutionele structuur:
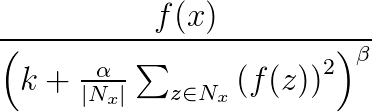
Antwoordnormalisatiebundels ondersteunen alle convolutionele kenmerken, behalve Delen, MapCount en Weights.
Als de kernel neuronen bevat in dezelfde kaart als x, wordt het normalisatieschema aangeduid als dezelfde kaartnormalisatie. Als u dezelfde toewijzingsnormalisatie wilt definiëren, moet de eerste coördinaat in InputShape de waarde 1 hebben.
Als de kernel neuronen bevat in dezelfde ruimtelijke positie als x, maar de neuronen zich in andere kaarten bevinden, wordt het normalisatieschema aangeroepen in kaartennormalisatie. Dit type reactienormalisatie implementeert een vorm van laterale remming geïnspireerd door het type dat in echte neuronen is gevonden, waardoor de concurrentie ontstaat voor grote activeringsniveaus tussen neuronuitvoer die op verschillende kaarten zijn berekend. Als u de normalisatie van kaarten wilt definiëren, moet de eerste coördinaat een geheel getal groter zijn dan één en niet groter zijn dan het aantal kaarten en moeten de rest van de coördinaten de waarde 1 hebben.
Omdat reactienormalisatiebundels een vooraf gedefinieerde functie toepassen op bronknooppuntwaarden om de waarde van het doelknooppunt te bepalen, hebben ze geen trainbare status (gewichten of vooroordelen).
Notitie
De knooppunten in de doellaag komen overeen met neuronen die de centrale knooppunten van de kernels zijn. Als dit bijvoorbeeld KernelShape[d] oneven is, komt dit KernelShape[d]/2 overeen met het centrale kernelknooppunt. Als KernelShape[d] het even is, bevindt het centrale knooppunt zich op KernelShape[d]/2 - 1. Padding[d] Als onwaar is, hebben de eerste en de laatste KernelShape[d]/2 knooppunten dus geen bijbehorende knooppunten in de doellaag. Om deze situatie te voorkomen, definieert u Opvulling als [true, true, ..., true].
Naast de vier kenmerken die eerder zijn beschreven, bieden antwoordnormalisatiebundels ook ondersteuning voor de volgende kenmerken:
- Alfa: (vereist) Hiermee geeft u een drijvende-kommawaarde op die overeenkomt met
αin de vorige formule. - Bèta: (vereist) Hiermee geeft u een drijvende-kommawaarde op die overeenkomt met
βde vorige formule. - Verschuiving: (optioneel) Hiermee geeft u een drijvende-kommawaarde op die overeenkomt met
kin de vorige formule. De standaardwaarde is 1.
In het volgende voorbeeld wordt een antwoordnormalisatiebundel gedefinieerd met behulp van deze kenmerken:
hidden RN1 [5, 10, 10]
from P1 response norm {
InputShape = [ 5, 12, 12];
KernelShape = [ 1, 3, 3];
Alpha = 0.001;
Beta = 0.75;
}
- De bronlaag bevat vijf kaarten, elk met een dimensie van 12x12, in totaal 1440 knooppunten.
- De waarde van KernelShape geeft aan dat dit dezelfde kaartnormalisatielaag is, waarbij de buurt een 3x3-rechthoek is.
- De standaardwaarde van Opvulling is Onwaar, dus de doellaag heeft slechts 10 knooppunten in elke dimensie. Als u één knooppunt wilt opnemen in de doellaag die overeenkomt met elk knooppunt in de bronlaag, voegt u Padding = [true, true, true]; en wijzig de grootte van RN1 in [5, 12, 12].
Declaratie delen
Net# ondersteunt optioneel het definiëren van meerdere bundels met gedeelde gewichten. De gewichten van twee bundels kunnen worden gedeeld als hun structuren hetzelfde zijn. De volgende syntaxis definieert bundels met gedeelde gewichten:
share-declaration:
share { layer-list }
share { bundle-list }
share { bias-list }
layer-list:
layer-name , layer-name
layer-list , layer-name
bundle-list:
bundle-spec , bundle-spec
bundle-list , bundle-spec
bundle-spec:
layer-name => layer-name
bias-list:
bias-spec , bias-spec
bias-list , bias-spec
bias-spec:
1 => layer-name
layer-name:
identifier
De volgende share-declaratie geeft bijvoorbeeld de laagnamen op, waarmee wordt aangegeven dat zowel gewichten als vooroordelen moeten worden gedeeld:
Const {
InputSize = 37;
HiddenSize = 50;
}
input {
Data1 [InputSize];
Data2 [InputSize];
}
hidden {
H1 [HiddenSize] from Data1 all;
H2 [HiddenSize] from Data2 all;
}
output Result [2] {
from H1 all;
from H2 all;
}
share { H1, H2 } // share both weights and biases
- De invoerfuncties worden gepartitioneerd in twee invoerlagen met gelijke grootte.
- De verborgen lagen berekenen vervolgens functies op een hoger niveau op de twee invoerlagen.
- De share-declaratie geeft aan dat H1 en H2 op dezelfde manier moeten worden berekend op basis van hun respectieve invoer.
U kunt dit ook als volgt opgeven met twee afzonderlijke share-declaraties:
share { Data1 => H1, Data2 => H2 } // share weights
<!-- -->
share { 1 => H1, 1 => H2 } // share biases
U kunt de korte vorm alleen gebruiken wanneer de lagen één bundel bevatten. Over het algemeen is delen alleen mogelijk wanneer de relevante structuur identiek is, wat betekent dat ze dezelfde grootte hebben, dezelfde convolutionele geometrie, enzovoort.
Voorbeelden van Net#-gebruik
Deze sectie bevat enkele voorbeelden van hoe u Net# kunt gebruiken om verborgen lagen toe te voegen, de manier te definiëren waarop verborgen lagen communiceren met andere lagen en convolutionele netwerken te bouwen.
Een eenvoudig aangepast neuraal netwerk definiëren: 'Hallo wereld'-voorbeeld
In dit eenvoudige voorbeeld ziet u hoe u een neuraal netwerkmodel maakt met één verborgen laag.
input Data auto;
hidden H [200] from Data all;
output Out [10] sigmoid from H all;
In het voorbeeld ziet u een aantal basisopdrachten als volgt:
- De eerste regel definieert de invoerlaag (benoemd
Data). Wanneer u hetautotrefwoord gebruikt, bevat het neurale netwerk automatisch alle functiekolommen in de invoervoorbeelden. - Met de tweede regel wordt de verborgen laag gemaakt. De naam
Hwordt toegewezen aan de verborgen laag, met 200 knooppunten. Deze laag is volledig verbonden met de invoerlaag. - De derde regel definieert de uitvoerlaag (benoemd
Out), die 10 uitvoerknooppunten bevat. Als het neurale netwerk wordt gebruikt voor classificatie, is er één uitvoerknooppunt per klasse. Het trefwoord sigmoid geeft aan dat de uitvoerfunctie wordt toegepast op de uitvoerlaag.
Meerdere verborgen lagen definiëren: Computer Vision-voorbeeld
In het volgende voorbeeld ziet u hoe u een iets complexer neuraal netwerk definieert, met meerdere aangepaste verborgen lagen.
// Define the input layers
input Pixels [10, 20];
input MetaData [7];
// Define the first two hidden layers, using data only from the Pixels input
hidden ByRow [10, 12] from Pixels where (s,d) => s[0] == d[0];
hidden ByCol [5, 20] from Pixels where (s,d) => abs(s[1] - d[1]) <= 1;
// Define the third hidden layer, which uses as source the hidden layers ByRow and ByCol
hidden Gather [100]
{
from ByRow all;
from ByCol all;
}
// Define the output layer and its sources
output Result [10]
{
from Gather all;
from MetaData all;
}
In dit voorbeeld ziet u verschillende functies van de specificatietaal voor neurale netwerken:
- De structuur heeft twee invoerlagen en
PixelsMetaData. - De
Pixelslaag is een bronlaag voor twee verbindingsbundels, met doellagenByRowenByCol. - De lagen
GatherenResultzijn doellagen in meerdere verbindingsbundels. - De uitvoerlaag,
Resultis een doellaag in twee verbindingsbundels; een met de tweede verborgen laagGatherop het tweede niveau als doellaag en de andere met de invoerlaag als doellaagMetaData. - De verborgen lagen
ByRowenByColgeef gefilterde connectiviteit op met behulp van predicaatexpressies. Om precies te zijn, wordt het knooppuntByRowop [x, y] verbonden met de knooppunten waarinPixelsde eerste indexcoördinaat gelijk is aan de eerste coördinaat van het knooppunt, x. Op dezelfde manier is het knooppuntByColop [x, y] verbonden met de knooppuntenPixelsmet de tweede indexcoördinaat binnen een van de tweede coördinaat van het knooppunt, y.
Definieer een convolutioneel netwerk voor classificatie met meerdere klassen: voorbeeld van cijferherkenning
De definitie van het volgende netwerk is ontworpen om getallen te herkennen en illustreert enkele geavanceerde technieken voor het aanpassen van een neuraal netwerk.
input Image [29, 29];
hidden Conv1 [5, 13, 13] from Image convolve
{
InputShape = [29, 29];
KernelShape = [ 5, 5];
Stride = [ 2, 2];
MapCount = 5;
}
hidden Conv2 [50, 5, 5]
from Conv1 convolve
{
InputShape = [ 5, 13, 13];
KernelShape = [ 1, 5, 5];
Stride = [ 1, 2, 2];
Sharing = [false, true, true];
MapCount = 10;
}
hidden Hid3 [100] from Conv2 all;
output Digit [10] from Hid3 all;
De structuur heeft één invoerlaag,
Image.Het trefwoord
convolvegeeft aan dat de benoemde lagenConv1enConv2convolutionele lagen zijn. Elk van deze laagdeclaraties wordt gevolgd door een lijst met de convolutiekenmerken.Het net heeft een derde verborgen laag,
Hid3die volledig is verbonden met de tweede verborgen laag,Conv2.De uitvoerlaag, is
Digitalleen verbonden met de derde verborgen laag,Hid3. Het trefwoordallgeeft aan dat de uitvoerlaag volledig is verbonden metHid3.De ariteit van de convolutie is drie: de lengte van de tuples
InputShape,KernelShape,StrideenSharing.Het aantal gewichten per kernel is
1 + KernelShape\[0] * KernelShape\[1] * KernelShape\[2] = 1 + 1 * 5 * 5 = 26. Of26 * 50 = 1300.U kunt de knooppunten in elke verborgen laag als volgt berekenen:
NodeCount\[0] = (5 - 1) / 1 + 1 = 5NodeCount\[1] = (13 - 5) / 2 + 1 = 5NodeCount\[2] = (13 - 5) / 2 + 1 = 5Het totale aantal knooppunten kan als volgt worden berekend met behulp van de gedeclareerde dimensionaliteit van de laag, [50, 5, 5]:
MapCount * NodeCount\[0] * NodeCount\[1] * NodeCount\[2] = 10 * 5 * 5 * 5Omdat
Sharing[d]is alleen onwaar voord == 0, het aantal kernels isMapCount * NodeCount\[0] = 10 * 5 = 50.
Erkenningen
De Net#-taal voor het aanpassen van de architectuur van neurale netwerken is ontwikkeld bij Microsoft door Shon Katzenberger (Architect, Machine Learning) en Alexey Kamenev (Software Engineer, Microsoft Research). Het wordt intern gebruikt voor machine learning-projecten en toepassingen, variërend van afbeeldingsdetectie tot tekstanalyse. Zie Neural Nets in Machine Learning Studio - Inleiding tot Net voor meer informatie #