Nuta
Dostęp do tej strony wymaga autoryzacji. Możesz spróbować zalogować się lub zmienić katalogi.
Dostęp do tej strony wymaga autoryzacji. Możesz spróbować zmienić katalogi.
Użyj przekształceń innych niż affine, aby obrócić obiekty 2D w przestrzeni 3D.
Jednym z typowych zastosowań przekształceń innych niż affine jest symulowanie obrotu obiektu 2D w przestrzeni 3D:
To zadanie obejmuje pracę z rotacjami trójwymiarowymi, a następnie wyprowadzanie transformacji nieaplikowanej SKMatrix , która wykonuje te rotacje 3D.
Trudno jest opracować tę SKMatrix transformację działającą wyłącznie w dwóch wymiarach. Zadanie staje się znacznie łatwiejsze, gdy ta macierz 3-by-3 pochodzi z macierzy 4-by-4 używanej w grafice 3D. SkiaSharp obejmuje klasę SKMatrix44 do tego celu, ale niektóre tło w grafice 3D jest niezbędne do zrozumienia rotacji 3D i macierzy transformacji 4-po 4.
Trójwymiarowy układ współrzędnych dodaje trzecią oś o nazwie Z. Koncepcyjnie oś Z znajduje się pod kątem prostym na ekranie. Punkty współrzędnych w przestrzeni 3D są wskazywane trzema liczbami: (x, y, z). W systemie współrzędnych 3D używanym w tym artykule zwiększenie wartości X jest na prawo i zwiększenie wartości Y spada, podobnie jak w dwóch wymiarach. Zwiększenie dodatnich wartości Z wychodzi z ekranu. Początek to lewy górny róg, podobnie jak w grafice 2D. Ekran można traktować jako płaszczyznę XY z osią Z pod kątami prostymi do tej płaszczyzny.
Jest to nazywane układem współrzędnych po lewej stronie. Jeśli wskażesz forefinger lewej strony w kierunku dodatnich współrzędnych X (z prawej strony), a środkowy palec w kierunku zwiększenia współrzędnych Y (w dół), to punkty kciuka w kierunku zwiększania współrzędnych Z — rozciągając się od ekranu.
W grafice 3D przekształcenia są oparte na macierzy 4-by-4. Oto macierz tożsamości 4-by-4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
W pracy z macierzą 4-by-4 wygodnie jest zidentyfikować komórki z ich numerami wierszy i kolumn:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Jednak klasa SkiaSharp Matrix44 jest nieco inna. Jedynym sposobem ustawiania lub pobierania poszczególnych wartości komórek jest SKMatrix44 użycie indeksatora Item . Indeksy wierszy i kolumn są oparte na zera, a nie na podstawie jednej, a wiersze i kolumny są zamieniane. Komórka M14 na powyższym diagramie jest dostępna przy użyciu indeksatora [3, 0]SKMatrix44 w obiekcie.
W systemie graficznym 3D punkt 3D (x, y, z) jest konwertowany na macierz 1-by-4 do mnożenia przez macierz przekształcania 4-by-4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Analogicznie do przekształceń 2D, które mają miejsce w trzech wymiarach, przyjmuje się, że przekształcenia 3D mają mieć miejsce w czterech wymiarach. Czwarty wymiar jest określany jako W, a przestrzeń 3D zakłada się, że istnieje w przestrzeni 4D, gdzie współrzędne W są równe 1. Formuły przekształcania są następujące:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Z formuł transformacji wynika, że komórki M11, M33M22, są czynnikami skalowania w kierunkach M42M41X, Y i Z oraz , i M43 są czynnikami tłumaczenia w kierunkach X, Y i Z.
Aby przekonwertować te współrzędne z powrotem na przestrzeń 3D, gdzie W równa 1, współrzędne x', y i z są dzielone przez w':
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Ten podział według w' zapewnia perspektywę w przestrzeni 3D. Jeśli wartość w jest równa 1, perspektywa nie występuje.
Rotacje w przestrzeni 3D mogą być dość złożone, ale najprostsze rotacje to te wokół osi X, Y i Z. Rotacja kąta α wokół osi X jest następująca macierz:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Wartości X pozostają takie same w przypadku poddania tej transformacji. Obrót wokół osi Y pozostawia wartości Y bez zmian:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
Obrót wokół osi Z jest taki sam jak w grafice 2D:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Kierunek obrotu jest implikowany przez przekazanie układu współrzędnych. Jest to system leworęczny, więc jeśli wskażesz kciuk lewej ręki w kierunku rosnących wartości dla określonej osi — po prawej stronie dla obrotu wokół osi X, w dół w celu obrotu wokół osi Y, a w kierunku obrotu wokół osi Z — krzywa innych palców wskazuje kierunek obrotu dla kątów dodatnich.
SKMatrix44 ma uogólnione metody statyczne CreateRotation i CreateRotationDegrees , które umożliwiają określenie osi, wokół której odbywa się obrót:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Dla obrotu wokół osi X ustaw pierwsze trzy argumenty na 1, 0, 0. Dla obrotu wokół osi Y ustaw je na 0, 1, 0 i dla obrotu wokół osi Z, ustaw je na 0, 0, 1.
Czwarta kolumna 4-by-4 jest dla perspektywy. Nie SKMatrix44 ma metod tworzenia przekształceń perspektyw, ale można utworzyć je samodzielnie przy użyciu następującego kodu:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
Przyczyna nazwy depth argumentu będzie widoczna wkrótce. Ten kod tworzy macierz:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Formuły przekształcania powodują następujące obliczenie elementu w':
w' = –z / depth + 1
Służy to do zmniejszenia współrzędnych X i Y, gdy wartości Z są mniejsze niż zero (koncepcyjnie za płaszczyzną XY) i zwiększyć współrzędne X i Y dla wartości dodatnich Z. Gdy współrzędna Z równa depth, wartość w' wynosi zero, a współrzędne stają się nieskończone. Trójwymiarowe systemy graficzne są zbudowane wokół metafory aparatu, a depth wartość reprezentuje odległość aparatu od źródła układu współrzędnych. Jeśli obiekt graficzny ma współrzędną Z, która jest depth jednostką pochodzenia, koncepcyjnie dotyka obiektywu aparatu i staje się nieskończenie duża.
Pamiętaj, że prawdopodobnie użyjesz tej perspectiveMatrix wartości w połączeniu z macierzami obrotowymi. Jeśli obracany obiekt graficzny ma współrzędne X lub Y większe niż depth, rotacja tego obiektu w przestrzeni 3D może obejmować współrzędne Z większe niż depth. Należy tego unikać! Podczas tworzenia perspectiveMatrix chcesz ustawić depth wartość wystarczająco dużą dla wszystkich współrzędnych w obiekcie graficznym niezależnie od tego, jak jest obracana. Gwarantuje to, że nigdy nie ma żadnego podziału o zero.
Połączenie obrotu 3D i perspektywy wymaga pomnożenia macierzy 4-by-4 razem. W tym celu SKMatrix44 definiuje metody łączenia. Jeśli A obiekty i B są SKMatrix44 obiektami, następujący kod ustawia wartość A równą A × B:
A.PostConcat(B);
Gdy macierz przekształcania 4-by-4 jest używana w systemie graficznym 2D, jest stosowana do obiektów 2D. Te obiekty są płaskie i zakłada się, że współrzędnych Z wynosi zero. Mnożenie transformacji jest nieco prostsze niż pokazana wcześniej transformacja:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Ta wartość 0 dla z powoduje przekształcenie formuł, które nie obejmują żadnych komórek w trzecim wierszu macierzy:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Co więcej, współrzędna z również nie ma znaczenia tutaj. Gdy obiekt 3D jest wyświetlany w systemie graficznym 2D, jest zwinięty do obiektu dwuwymiarowego, ignorując wartości współrzędnych Z. Formuły przekształcania są naprawdę tylko tymi dwoma:
x" = x' / w'
y" = y' / w'
Oznacza to, że trzeci wiersz i trzecia kolumna macierzy 4-by-4 mogą być ignorowane.
Ale jeśli tak jest, dlaczego macierz 4-by-4 jest nawet niezbędna w pierwszej kolejności?
Mimo że trzeci wiersz i trzecia kolumna 4-by-4 są nieistotne dla przekształceń dwuwymiarowych, trzeci wiersz i kolumna odgrywają rolę przed tym, gdy różne SKMatrix44 wartości są mnożone razem. Załóżmy na przykład, że pomnożysz rotację wokół osi Y za pomocą przekształcenia perspektywy:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
W produkcie komórka M14 zawiera teraz wartość perspektywy. Jeśli chcesz zastosować tę macierz do obiektów 2D, trzeci wiersz i kolumna zostaną wyeliminowane, aby przekonwertować ją na macierz 3-by-3:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Teraz można go użyć do przekształcenia punktu 2D:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Formuły przekształcania to:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Teraz podziel wszystko przez z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Gdy obiekty 2D są obracane z dodatnim kątem wokół osi Y, wartości dodatnie X cofają się do tła, podczas gdy ujemne wartości X przychodzą na pierwszy plan. Wartości X wydają się zbliżać do osi Y (która jest określana przez wartość cosinus) jako współrzędne najdalej z osi Y staje się mniejsza lub większa, gdy przesuwają się dalej z przeglądarki lub bliżej osoby przeglądającego.
W przypadku korzystania z programu SKMatrix44wykonaj wszystkie operacje obrotu 3D i perspektywy, mnożąc różne SKMatrix44 wartości. Następnie można wyodrębnić dwuwymiarową macierz 3-by-3 z macierzy 4-by-4 przy użyciu Matrix właściwości SKMatrix44 klasy . Ta właściwość zwraca znaną SKMatrix wartość.
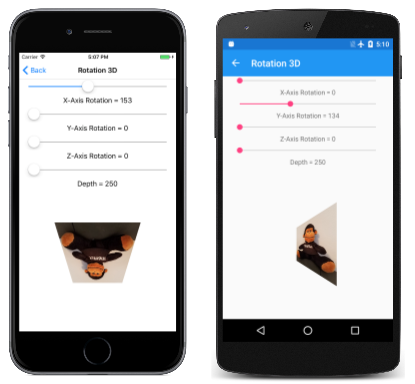
Strona Rotacja 3D umożliwia eksperymentowanie z rotacją 3D . Plik Rotation3DPage.xaml tworzy cztery suwaki, aby ustawić obrót wokół osi X, Y i Z oraz ustawić wartość głębokości:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Zwróć uwagę, że element depthSlider jest inicjowany z wartością Minimum 250. Oznacza to, że obracany w tym miejscu obiekt 2D ma współrzędne X i Y ograniczone do okręgu zdefiniowanego przez promień 250 pikseli wokół źródła. Każda rotacja tego obiektu w przestrzeni 3D zawsze spowoduje współrzędnych wartości mniejszych niż 250.
Plik Rotation3DPage.cs za pomocą kodu ładuje się w mapie bitowej, która ma 300 pikseli kwadratowych:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Jeśli transformacja 3D jest wyśrodkowana na tej mapie bitowej, współrzędne X i Y wahają się od –150 do 150, podczas gdy narożniki są 212 pikseli od środka, więc wszystko znajduje się w promieniu 250 pikseli.
Procedura PaintSurface obsługi tworzy SKMatrix44 obiekty na podstawie suwaków i mnoży je razem przy użyciu polecenia PostConcat. SKMatrix Wartość wyodrębniona z obiektu końcowego SKMatrix44 jest otoczona przetłumaczeniami, aby wyśrodkować obrót w środku ekranu:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Podczas eksperymentowania z czwartym suwakiem zauważysz, że różne ustawienia głębokości nie przenoszą obiektu dalej od przeglądarki, ale zmieniają zakres efektu perspektywy:
Animowany obrót 3D używa SKMatrix44 również do animowania ciągu tekstowego w przestrzeni 3D. Obiekt textPaint ustawiony jako pole jest używany w konstruktorze w celu określenia granic tekstu:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Przesłonięcia OnAppearing definiują trzy Xamarin.FormsAnimation obiekty, aby animować xRotationDegreespola , yRotationDegreesi zRotationDegrees w różnych stawkach. Zwróć uwagę, że okresy tych animacji są ustawione na liczby pierwsze (5 sekund, 7 sekund i 11 sekund), więc ogólna kombinacja powtarza się tylko co 385 sekund lub więcej niż 10 minut:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Podobnie jak w poprzednim programie program PaintCanvas obsługi tworzy SKMatrix44 wartości dla rotacji i perspektywy i mnoży je razem:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Ta rotacja 3D jest otoczona kilkoma transformacjami 2D, aby przenieść środek obrotu do środka ekranu i skalować rozmiar ciągu tekstowego, tak aby była taka sama szerokość jak ekran: