Tworzenie splątania kwantowego za pomocą polecenia Q#

7 min

W poprzedniej lekcji przedstawiono koncepcję splątania kwantowego i stanów Bell.

Teraz utwórzmy splątanie kwantowe przy użyciu i Q# platformy Azure Quantum Development Kit. Aby utworzyć splątanie, należy zastosować dwie operacje kwantowe: bramę Hadamard i bramę Controlled-NOT (CNOT).

Operacja Kontrolowana NOT (CNOT)

Gdy dwa kubity są splątane, stan jednego kubitu zależy od stanu drugiego kubitu. W związku z tym w celu splątania dwóch kubitów potrzebna jest operacja działająca na obu kubitach jednocześnie. Jest to nazywane operacją wielokątną.

Aby utworzyć splątanie kwantowe, potrzebna jest operacja wielokabitowa CNOT , która oznacza Controlled-NOT. Ta operacja przyjmuje dwa kubity jako dane wejściowe, jeden działa jako kubit kontrolny, a drugi to target kubit. Operacja CNOT przerzuca stan drugiego kubitu (kubitu target ), jeśli i tylko wtedy, gdy stan pierwszego kubitu (kubitu sterującego) wynosi $|1\rangle$.

Dane wejściowe	Dane wyjściowe
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

W Q#systemie CNOT operacja działa na tablicy dwóch kubitów i przerzuca drugi kubit, jeśli pierwszy kubit to One.

Splątanie za pomocą operacji CNOT

Stosując operację Hadamard, , i Controlled-NOT, CNOT, operację, można przekształcić dwa kubity w stanie $|00\rangle$ do stanu $\ket{\phiBell ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$. H

Oto, jak to działa:

Weź dwa kubity w stanie $|00\rangle$. Pierwszy kubit to kubit kontrolny, a drugi kubit to target kubit.
Utwórz stan superpozycji tylko w kubitie sterującym $, stosując H$.

$$H |0_c\rangle={2}}\frac{1}{\sqrt{(|0_c\rangle+|1_c)\rangle$$

Uwaga

Indeksy ${}dolny _c$ i ${}_t$ określają kontrolkę i target kubity.
$Zastosuj operator CNOT$ do kubitu sterującego, który znajduje się w stanie superpozycji i target kubitu, który znajduje się w stanie $|0_t\rangle$.

$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c+\ket{1_c})\ket{0}_t =}CNOT \frac{1}{\sqrt2}(0_c 0_t+|\ket{1_c 0_t}})==\frac{$${1}{\sqrt$$2(\ket{CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})$$=\frac{1}{\sqrt$$=2}}(\ket{0_c 0_t}+\ket{1_c 1_t)}$$

Tworzenie nowego Q# pliku

Otwórz Visual Studio Code.
Wybierz pozycję Plik > nowy plik tekstowy i zapisz go jako Main.qs.
Wybierz pozycję Widok —> Paleta poleceń i wpisz Q#: Ustaw profil usługi Azure Quantum QIRtarget. Naciśnij klawisz Enter.
Wybierz pozycję Q#: Bez ograniczeń.

Tworzenie i mierzenie stanu $\ket{\phidzwonka ^+}$

Zacznijmy od utworzenia stanu $\ket{\phidzwonka ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Utwórz stan $\ket{\phidzwonka ^+}$ w Q#

Najpierw należy zaimportować Microsoft.Quantum.Diagnostics przestrzeń nazw z biblioteki standardowej, która zawiera DumpMachine funkcję . Ta funkcja pokazuje bieżący stan kubitów. Skopiuj i wklej następujący Q# kod do pliku Main.qs .
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
Napiwek

Możesz również zaimportować bibliotekę Standardowa, podstawiając Microsoft.Quantum Stdelement . Na przykład instrukcja import Std.Diagnostics.* jest równoważna instrukcji import Microsoft.Quantum.Diagnostics.*.

Utwórz operację Main zwracającą dwie Result wartości typu, które są wynikami pomiaru kubitów.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

Main Wewnątrz operacji należy przydzielić dwa kubity i q1 q2, które będą splątane.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

Zastosuj bramę Hadamard, , Hdo pierwszego kubitu, q1, aby umieścić go w stanie superpozycji. Następnie splątanie dwóch kubitów przy użyciu CNOT operacji .

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}

DumpMachine Użyj funkcji , aby wyświetlić bieżący stan kubitów. Nie jest to samo, co pomiar kubitów.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

Zmierz kubity przy użyciu M operacji i zapisz wyniki w m1 elementach i m2. Następnie użyj Reset operacji , aby zresetować kubity. W Q#systemie należy zawsze resetować kubity do $|stanu 0\rangle$ .

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

Na koniec zwróć wyniki pomiaru kubitów z instrukcją return . Plik Main.qs powinien wyglądać następująco:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Uruchamianie programu

Aby uruchomić program w wbudowanym symulatorze, kliknij pozycję Uruchom nad operacją Main lub naciśnij Ctrl+F5. Dane wyjściowe zostaną wyświetlone w konsoli debugowania.
Wyniki pomiaru są skorelowane, więc na końcu programu uzyskasz wynik (Zero, Zero) lub (One, One) z równym prawdopodobieństwem.
Diagram obwodu można wizualizować, klikając pozycję Obwód z listy poleceń powyżej Main operacji. Diagram obwodu przedstawia bramę Hadamard zastosowaną do pierwszego kubitu i bramę CNOT zastosowaną do obu kubitów.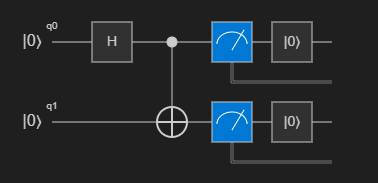

Tworzenie i mierzenie stanu $\ket{\phidzwonka ^-}$

Aby utworzyć inne stany Bell, należy zastosować dodatkowe operacje Pauli $X$ i $Z$ do kubitów.

Aby na przykład utworzyć stan $\ket{\phiBell ^-}=\frac1{\sqrt2}(|00-11|\rangle\rangle)$, możesz zastosować operację Pauli $Z$ do kubitu kontrolnego po zastosowaniu bramy Hadamard. Operacja $Z$ przerzuca stan $\ket{+}$ na $\ket{-}$.

Uwaga

Stany $\frac{(0+|1\rangle)$ i $\frac{1}{\sqrt{{2}}(|0\rangle\rangle -|1\rangle)$ są również znane odpowiednio jako $\ket{+}$ i .{-}$$\ket{|{1}{\sqrt{2}}

Oto, jak to działa:

Weź dwa kubity w stanie $|00\rangle$.
Utwórz stan superpozycji tylko w kubitie sterującym $, stosując H$.

$$H |0_c\frac{\rangle={1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+_c}$$
Zastosuj operację $Z$ do kubitu sterującego.

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)\frac{1}{\sqrt{={2}}(|0_c-1_c\rangle|)_c\rangle=\ket{{-}$$
$Zastosuj operator CNOT$ do kubitu sterującego i kubitutarget, który znajduje się w stanie $|0_t\rangle$.

$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c-1_c\ket{})_t}= CNOT \frac{1}{\sqrt2}(0_c 0_t-1_c 0_t}|\ket{})$$=$$\ket{0}=\frac{{1}{\sqrt2}(\ket{CNOT \ket{0_c 0_t} — CNOT \ket{1_c 0_t})$$\frac{1}{\sqrt=$$=2}(\ket{0_c 0_t-1_c 1_t)}\ket{}$$

Utwórz stan $\ket{\phidzwonka ^-}$ w Q#

Zmodyfikuj kod, Q# aby utworzyć stan $\ket{\phibell ^-}$. Plik Main.qs powinien wyglądać następująco:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Aby uruchomić program w wbudowanym symulatorze, kliknij pozycję Uruchom nad operacją Main lub naciśnij Ctrl+F5. Dane wyjściowe zostaną wyświetlone w konsoli debugowania.
Diagram obwodu można wizualizować, klikając pozycję Obwód z listy poleceń powyżej Main operacji. Diagram obwodu przedstawia bramę Hadamard zastosowaną do pierwszego kubitu, bramę Pauli $Z$ zastosowaną do pierwszego kubitu i bramę CNOT zastosowaną do obu kubitów.

Ćwiczenie dodatkowe: Tworzenie stanów $\ket{\psiBell ^+}$ i $\ket{\psi^-}$

Podobnie stany $\ket{\psiBell ^+}$ i $\ket{\psi^-}$ można utworzyć, stosując operacje Pauli $X$ i $Z$ do kubitów.

Stan $\ket{\psibell ^+}=\frac1{\sqrt2}(|01+|10\rangle\rangle)$ można utworzyć, stosując operację Pauli $X$ do kubitu po zastosowaniu target bramy Hadamard.
Stan $\ket{\psiBell ^-}=\frac1{\sqrt2}(|01-10\rangle\rangle|)$ można utworzyć, stosując Pauli Z$ do kubitu kontrolnego i Pauli $$X$ do kubitu target po zastosowaniu bramy Hadamard.

Zmodyfikuj program Main.qs, aby utworzyć stany $\ket{\psiBell ^+}$ i $\ket{\psi^-}$.