Co to jest superpozycja w obliczeniach kwantowych?
W świecie klasycznym rzeczywiste obiekty, takie jak kot i pudełko, mogą znajdować się tylko w jednym stanie naraz. Ale w świecie kwantowym cząstki mogą istnieć w superpozycji wszystkich możliwych stanów.
Niestety, nie ma żadnych komputerów kwantowych, które używają kotów do wykonywania obliczeń. Zamiast tego rzeczywiste komputery kwantowe używają kubitów, skrót od bitów kwantowych. Podobnie jak w jaki sposób bit jest podstawową jednostką informacji w obliczeniach klasycznych, kubit jest podstawową jednostką informacji w obliczeniach kwantowych. I tak jak bity mogą przyjmować jedną z dwóch możliwych wartości, 0 i 1, kubit ma również wartość 0 lub 1 podczas mierzenia.
Istnieje wiele fizycznych reprezentacji kubitów. Na przykład polaryzacja fotonu lub spin elektronu może być używana jako kubity, ponieważ fotony mają dwa odrębne stany polaryzacji, a elektrony mają dwa odrębne stany spinu, gdy je mierzymy. Możemy reprezentować jeden z tych stanów jako 0, a drugi jako 1, a kubit zawsze daje 0 lub 1, gdy ją mierzymy.
Jak jednak reprezentujemy superpozycję w kubitie? A jakie jest prawdopodobieństwo, że uważamy kubit za określony stan, gdy bierzemy pomiar?
Reprezentacja sfery Bloch superpozycji dla pojedynczych kubitów
Kubit to cząstka kwantowa, która znajduje się w jednym z dwóch możliwych stanów podczas mierzenia kubitu. Niezależnie od fizycznego charakteru kubitu oznaczamy dwa stany jako 0 i 1. Kubit może być w stanie 0, w stanie 1 lub w nieskończonej liczbie superpozycji stanów 0 i 1. Jak przedstawiamy te superpozycje w obliczeniach kwantowych?
Przydatną geometryczną reprezentacją stanu superpozycji pojedynczego kubitu jest sfera Blocha.
Załóżmy, że narysujesz okrąg z promieniem jednostki (długość promienia równa 1). Następnie narysuj oś pionową i poziomą, tak aby dwie osie przecinały się w środku okręgu. Teraz zdefiniujmy stan 0, w którym oś pionowa spełnia górną część okręgu, a 1 stan, w którym oś pionowa spełnia dolną część okręgu. W tym okręgu stany 0 i 1 są oddalone o $180^\circ$, albo $\pi$ radian od siebie.
W jaki sposób ta reprezentacja jest związana ze stanem kubitu? Możemy reprezentować stan kubitu za pomocą strzałki (lub wektora) o długości jednostkowej, która jest rysowana od środka okręgu do krawędzi okręgu. Gdy wektor wskazuje w pionie w górę, kubit znajduje się w stanie 0, a gdy wektor wskazuje pionowo w dół, kubit znajduje się w stanie 1. W tej reprezentacji klasyczny bit będzie wektorem, który zawsze wskazuje prosto w górę lub prosto w dół, ale nigdy w żadnym innym kierunku.
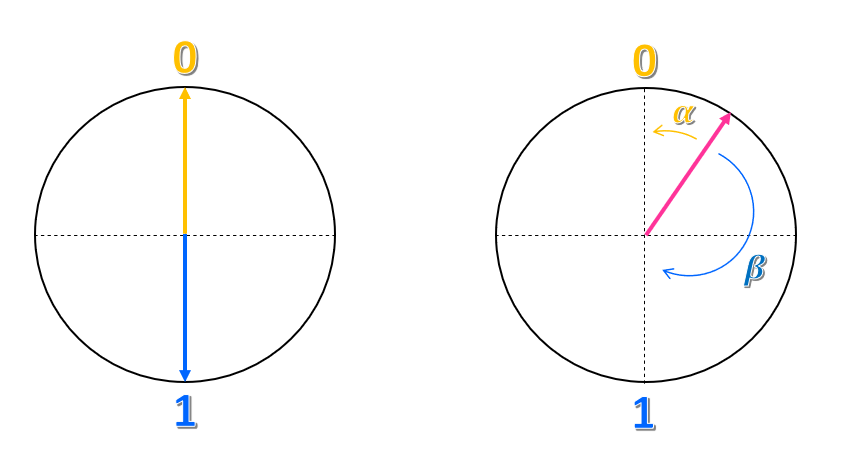
W przypadku kubitu wektor może wskazywać dowolne miejsce w okręgu. Każda lokalizacja w okręgu, inna niż prosta w górę lub prosto w dół, reprezentuje stan superpozycji. Na przykład nazywamy kątem, który wektor tworzy ze stanem 0 $\alpha$, i kątem, który wektor tworzy z 1 stanem $\beta$. Następnie reprezentujemy stan superpozycji kubitu jako $\alpha 0 + \beta 1$.
Podobnie jak w przykładzie kota i pola, stan superpozycji kubitu jest sumą poszczególnych stanów, 0 i 1, ważonych przez liczby $\alpha$ i $\beta$. Jednak w systemie cat-and-box wagi są liczbami rzeczywistymi, ale w systemie kubitów wagi $\alpha$ i $\beta$ są liczbami zespolonymi.
Ponieważ amplitudy $\alpha$ i $\beta$ są liczbami zespolonymi, potrzebujemy innego okręgu na naszym diagramie, który znajduje się w prostopadle płaszczyzny do pierwszego okręgu, aby naprawdę reprezentować każdy stan superpozycji kubitu. Te dwa okręgi istnieją w trzech wymiarach, aby stworzyć sferę Blocha.
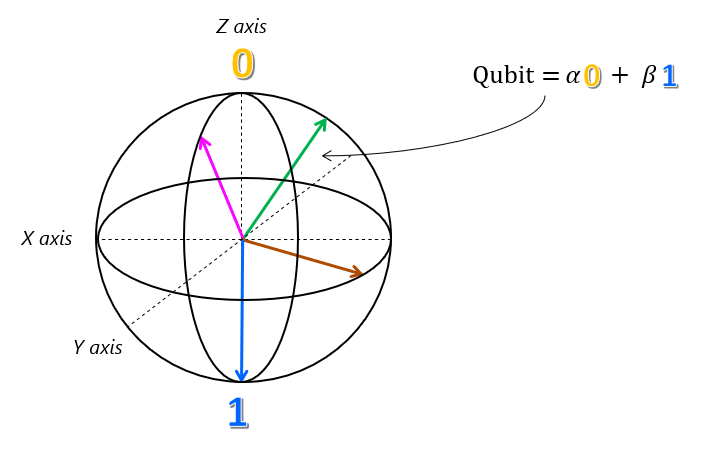
Ta sfera Bloch jest dokładną geometryczną reprezentacją każdego możliwego stanu superpozycji dla pojedynczego kubitu. Stan kubitu jest reprezentowany przez lokalizację na powierzchni sfery, na którą wskazuje wektor. Tak przydatne, jak sfera Blocha, niestety nie można go rozszerzyć na systemy z wieloma kubitami.
Napiwek
Sfera Bloch jest zaawansowanym narzędziem, ponieważ operacje wykonywane na kubitie podczas obliczeń kwantowych są reprezentowane jako rotacje o jednej z osi kardynalnych sfery Blocha. Ta geometryczna reprezentacja pomaga zbudować intuicję dotyczącą sposobu działania operacji w obliczeniach kwantowych, ale trudno jest użyć tej intuicji do projektowania i opisywania algorytmów. Język Q# pomaga, udostępniając język opisujący takie rotacje.
Jakie jest prawdopodobieństwo znalezienia kubitu w określonym stanie?
W systemie cat-and-box z poprzedniej lekcji wagi dla każdego stanu to liczby rzeczywiste, które bezpośrednio odpowiadają prawdopodobieństwo, że system znajduje się w każdym stanie. W systemie kubitów liczby $\alpha$ i $\beta$ są ogólnie liczbami złożonymi, które nie dają bezpośrednio prawdopodobieństwa znalezienia kubitu w stanach 0 i 1. Zamiast tego te liczby są nazywane amplitudami prawdopodobieństwa (lub po prostu amplitudami).
Rzeczywiste prawdopodobieństwa są obliczane na podstawie kwadratów wielkości amplitud prawdopodobieństwa. Prawdopodobieństwo znalezienia kubitu w stanie 0 wynosi $|\alpha|^2$, a prawdopodobieństwo znalezienia kubitu w stanie 1 wynosi $|\beta|^2$. Ogólnie rzecz biorąc, $\alpha + \beta$ nie sumuje się do 100%, ale $|\alpha|^2 + |\beta|^2$ zawsze tak jest. Ograniczenie, które $|\alpha|^2 + |\beta|^2 = 1$ jest nazywane warunkiem normalizacji, a każdy prawidłowy stan kwantowy musi spełniać ten warunek.