Przekształcanie projekcji (Direct3D 9)

Transformację projekcji można traktować jako kontrolowanie wewnętrznych aparatów; jest analogiczny do wybierania obiektywu dla aparatu. Jest to najbardziej skomplikowane z trzech typów transformacji. Ta dyskusja na temat transformacji projekcji jest zorganizowana w następujące tematy.

Macierz projekcji jest zwykle projekcją skali i perspektywy. Transformacja projekcji konwertuje frustum wyświetlania na kształt cuboid. Ponieważ bliski koniec frustum wyświetlania jest mniejszy niż daleko, ma to wpływ na rozszerzanie obiektów znajdujących się w pobliżu kamery; W ten sposób perspektywa jest stosowana do sceny.

W frustum oglądania, odległość między aparatem a źródłem przestrzeni przekształcania wyświetlania jest definiowana dowolnie jako D, więc macierz projekcji wygląda jak na poniższej ilustracji.

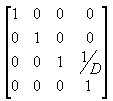
Macierz wyświetlania tłumaczy kamerę na początek, tłumacząc w kierunku z - D. Macierz tłumaczenia jest podobna do poniższej ilustracji.

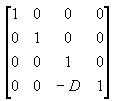
Pomnożenie macierzy tłumaczenia przez macierz projekcji (T*P) daje macierz projekcji złożonej, jak pokazano na poniższej ilustracji.

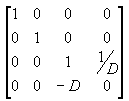
Przekształcenie perspektywy konwertuje frustum wyświetlania na nową przestrzeń współrzędnych. Zwróć uwagę, że frustum staje się podbuboidem, a także, że pochodzenie przenosi się z prawego górnego rogu sceny do środka, jak pokazano na poniższym diagramie.

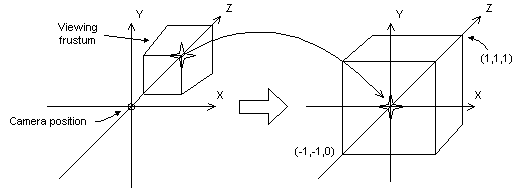
W transformacji perspektywy limity kierunku x i y są -1 i 1. Granice kierunku z są 0 dla płaszczyzny przedniej i 1 dla płaszczyzny tylnej.

Ta macierz tłumaczy i skaluje obiekty na podstawie określonej odległości od aparatu do bliskiej płaszczyzny wycinków, ale nie uwzględnia pola widoku (fov), a wartości z generowane dla obiektów w odległości mogą być prawie identyczne, co utrudnia porównywanie głębokości. Poniższa macierz rozwiązuje te problemy i dostosowuje wierzchołki, aby uwzględnić współczynnik proporcji widoku, co czyni go dobrym wyborem dla projekcji perspektywy.

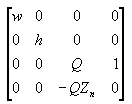
W tej macierzy Zn jest wartością z bliskiej płaszczyzny wycinków. Zmienne w, h i Q mają następujące znaczenie. Należy pamiętać, że fov_w i fovk reprezentują poziome i pionowe pola widoku widoku w radianach.

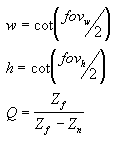
W przypadku aplikacji użycie kątów pola widoku do zdefiniowania współczynników x i y skalowania może nie być tak wygodne, jak użycie wymiarów poziomych i pionowych widoku (w przestrzeni aparatu). Jak działa matematyka, następujące dwa równania dla w i h używają wymiarów viewport i są równoważne z poprzednimi równaniami.

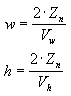
W tych formułach Zn reprezentuje położenie bliskiej płaszczyzny wycinków, a zmienne V_w i Vh reprezentują szerokość i wysokość widoku w przestrzeni aparatu.

W przypadku aplikacji języka C++ te dwa wymiary odpowiadają bezpośrednio członkom szerokości i wysokości struktury D3DVIEWPORT9.

Niezależnie od formuły, której zdecydujesz się użyć, ustaw wartość Zn na tak dużą, jak to możliwe, ponieważ wartości z bardzo blisko aparatu nie różnią się znacznie. Dzięki temu porównania głębokości przy użyciu 16-bitowych z są nieco skomplikowane.

Podobnie jak w przypadku transformacji świata i wyświetlania, należy wywołać metodę IDirect3DDevice9::SetTransform, aby ustawić transformację projekcji.

Konfigurowanie macierzy projekcji

Poniższa przykładowa funkcja ProjectionMatrix ustawia płaszczyzny przycinania przedniego i tylnego, a także poziome i pionowe pole kątów widzenia. Pola widoku powinny być mniejsze niż radiany pi.

D3DXMATRIX 
ProjectionMatrix(const float near_plane, // Distance to near clipping 
                                         // plane
                 const float far_plane,  // Distance to far clipping 
                                         // plane
                 const float fov_horiz,  // Horizontal field of view 
                                         // angle, in radians
                 const float fov_vert)   // Vertical field of view 
                                         // angle, in radians
{
    float    h, w, Q;

    w = (float)1/tan(fov_horiz*0.5);  // 1/tan(x) == cot(x)
    h = (float)1/tan(fov_vert*0.5);   // 1/tan(x) == cot(x)
    Q = far_plane/(far_plane - near_plane);

    D3DXMATRIX ret;
    ZeroMemory(&ret, sizeof(ret));

    ret(0, 0) = w;
    ret(1, 1) = h;
    ret(2, 2) = Q;
    ret(3, 2) = -Q*near_plane;
    ret(2, 3) = 1;
    return ret;
}   // End of ProjectionMatrix

Po utworzeniu macierzy ustaw ją przy użyciu IDirect3DDevice9::SetTransform określania D3DTS_PROJECTION.

Biblioteka narzędzi D3DX udostępnia następujące funkcje ułatwiające skonfigurowanie macierzy projekcji.

• D3DXMatrixPerspectiveLH
• D3DXMatrixPerspectiveRH
• D3DXMatrixPerspectiveFovLH
• D3DXMatrixPerspectiveFovRH
• D3DXMatrixPerspectiveOffCenterLH
• D3DXMatrixPerspectiveOffCenterRH

Macierz projekcji przyjazna dla W

Funkcja Direct3D może używać składnika w wierzchołka, który został przekształcony przez macierze świata, widoku i projekcji w celu wykonywania obliczeń na podstawie głębokości w buforze głębi lub efektach mgły. Obliczenia, takie jak te, wymagają, aby macierz projekcji znormalizowała wartość w, aby odpowiadała przestrzeni światowej z. Krótko mówiąc, jeśli macierz projekcji zawiera współczynnik (3,4), który nie jest 1, należy skalować wszystkie współczynniki przez odwrotność współczynnika (3,4), aby utworzyć właściwą macierz. Jeśli nie udostępnisz zgodnej macierzy, efekty mgły i buforowanie głębokości nie są stosowane poprawnie.

Poniższa ilustracja przedstawia niezgodną macierz projekcji i tę samą macierz skalowaną tak, aby mgła względna wzroku była włączona.

W poprzednich macierzach przyjmuje się, że wszystkie zmienne są niezerowe. Aby uzyskać więcej informacji na temat mgły względnej oczu, zobacz Eye-Relative vs. Z-Based Depth. Aby uzyskać informacje o buforowaniu głębokości opartej na systemie, zobacz głębokości (Direct3D 9).

Funkcja Direct3D używa obecnie ustawionej macierzy projekcji w obliczeniach głębokości opartych na w. W związku z tym aplikacje muszą ustawić zgodną macierz projekcji, aby otrzymywać żądane funkcje oparte na w, nawet jeśli nie używają funkcji Direct3D do transformacji.

Tematy pokrewne

przekształcenia