Equações PRT (Direct3D 9)

  • Artigo
  • 2 minutos para o fim da leitura

Para entender completamente um sombreador que implementa PRT, é útil derivar a fórmula que o sombreador usa para calcular o radiamento de saída.

Para começar, a equação a seguir é a equação geral para calcular o radiamento de saída resultante da iluminação direta em um objeto difuso com iluminação distante arbitrária.

equation of the exit radiance resulting from direct lighting on a diffuse object with arbitrary distant lighting

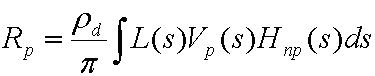
em que:

Parâmetro Descrição
Rp O radiamento de saída no vértice p. Avaliado em cada vértice na malha.
pd O albedo da superfície.
pi Uma constante, usada como um fator de normalização de conservação de energia.
L(s) O ambiente de iluminação (radiação de origem).
Vp₍s₎ Uma função de visibilidade binária para o ponto p. É 1 se o ponto pode ver a luz, 0 se não.
Hnp₍s₎ O termo cosseno da lei de Lambert. Igual a max(np> s), 0) em que Np é a superfície normal no ponto p.
s A variável que se integra sobre a esfera.

 

Usando funções de base esféricas, como harmônicos esféricos, a equação a seguir aproxima o ambiente de iluminação.

equation of the lighting environment

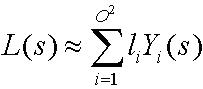
em que:

Parâmetro Descrição
L(s) O ambiente de iluminação (radiação de origem).
i Um inteiro que soma o número de funções de base.
O A ordem das harmônicas esféricas.
li Um coeficiente.
Yi(s) Alguma função de base sobre a esfera.

 

A coleção desses coeficientes, L', fornece a aproximação ideal para a função L(s) com as funções de base Y(s). Substituir e distribuir produz a equação a seguir.

equation of the exit radiance after substituting l(s) and distributing

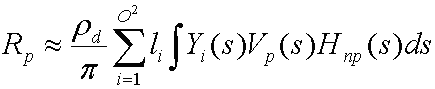
O integral do Yi(s)Vp₍s₎Hnp₍s₎ é um tpi de coeficiente de transferência que o simulador pré-compila para cada vértice na malha. Substituir isso gera a equação a seguir.

equation of the exit radiance after substituting the transfer coefficient

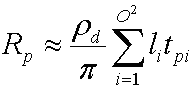
Alterar isso para notação de vetor gera a seguinte equação não compactada para calcular o radiamento de saída para cada canal.

equation of the exit radiance after changing to vector notation

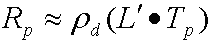
em que:

Parâmetro Descrição
Rp O radiamento de saída no vértice p.
pd O albedo da superfície.
L' O vetor de li e é a projeção do radiance de origem nas funções de base harmônica esféricas. Este é um vetor order² de coeficientes harmônicos esféricos.
Tp Um vetor de transferência order² para vértice p. O simulador divide os coeficientes de transferência por p.

 

Ambos os vetores são um vetor order² de coeficientes harmônicos esféricos, portanto, observe que este é simplesmente um produto de ponto. Dependendo da ordem, o ponto pode ser caro para que a compactação possa ser usada. Um algoritmo chamado CPCA (Clustered Principal Component Analysis) compacta os dados com eficiência. Isso permite o uso de uma aproximação harmônica esférica de ordem superior que resulta em sombras mais nítidas.

CPCA fornece a equação a seguir para aproximar o vetor de transferência.

equation of the approximated transfer vector

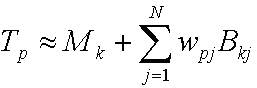
em que:

Parâmetro Descrição
Tp O vetor de transferência para o vértice p.
Mk A média do cluster k.
j Um inteiro que soma o número de vetores de PCA.
N O número de vetores de PCA.
wpj O peso jth PCA para o ponto p.
Bkj O vetor de base jth PCA para cluster k.

 

Um cluster é simplesmente um número de vértices que compartilham o mesmo vetor médio. Como obter a média do cluster, os pesos PCA, os vetores de base PCA e as IDs de cluster para os vértices são discutidos abaixo.

Substituir essas duas equações gera:

equation of the exit radiance after substituting the transfer vector

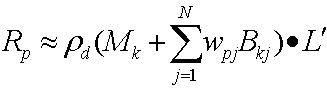
Em seguida, a distribuição do produto de ponto produz a equação a seguir.

equation of the exit radiance after distributing the dot product

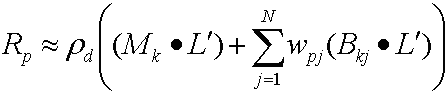
Porque ambos (Mk) L') e (Bkj> L') são constantes por vértice, o exemplo calcula esses valores com a CPU e os passa como constantes para o sombreador de vértice; porque o wpj muda para cada vértice, o exemplo armazena esses dados por vértice no buffer de vértice.

Transferência de radiação pré-compilada