Apêndice: Transformações de Matriz

Este tópico fornece uma visão geral matemática das transformações de matriz para gráficos 2D. No entanto, você não precisa saber matemática de matriz para usar transformações no Direct2D. Leia este tópico se você estiver interessado em matemática; caso contrário, fique à vontade para ignorar este tópico.

• introdução às matrizes
  • de Operações de Matriz
• de Transformações de Affine
  • de Transformação de Tradução
  • de Transformação de Dimensionamento
  • rotação em torno do de origem
  • rotação em torno de um ponto arbitrário
  • de Transformação de Distorção
• que representam transformações no Direct2D
• próximo

Introdução às Matrizes

Uma matriz é uma matriz retangular de números reais. A ordem da matriz é o número de linhas e colunas. Por exemplo, se a matriz tiver 3 linhas e 2 colunas, a ordem será 3 × 2. As matrizes geralmente são mostradas com os elementos de matriz entre colchetes:

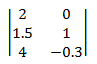
Notação: uma matriz é designada por uma letra maiúscula. Os elementos são designados por letras minúsculas. Os subscritos indicam o número de linha e coluna de um elemento. Por exemplo, umij é o elemento na coluna i'th row e j'th da matriz A.

O diagrama a seguir mostra uma matriz i × j, com os elementos individuais em cada célula da matriz.

Operações de matriz

Esta seção descreve as operações básicas definidas em matrizes.

Adição. A soma A + B de duas matrizes é obtida adicionando os elementos correspondentes de A e B:

A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]

multiplicação escalar. Essa operação multiplica uma matriz por um número real. Dado um número real k, o kA do produto escalar é obtido multiplicando cada elemento de A por k.

kA = k\[ a*ij* \] = \[ k × a*ij* \]

de multiplicação de matriz. Considerando duas matrizes A e B com ordem (m × n) e (n × p), o produto C = A × B é uma matriz com ordem (m × p), definida da seguinte maneira:

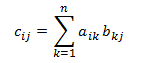
ou, equivalentemente:

c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*

Ou seja, para calcular cada elemento cij, faça o seguinte:

1. Pegue a i'th linha de A e a coluna j'th de B.
2. Multiplique cada par de elementos na linha e coluna: a entrada da primeira linha pela primeira entrada de coluna, a entrada da segunda linha pela segunda entrada de coluna e assim por diante.
3. Somar o resultado.

Aqui está um exemplo de multiplicação de uma matriz (2 × 2) por uma matriz (2 × 3).

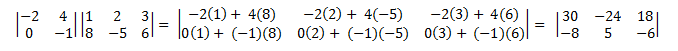
Multiplicação de matriz não é commutativa. Ou seja, A × B ≠ B × A. Além disso, na definição a seguir, nem todos os pares de matrizes podem ser multiplicados. O número de colunas na matriz esquerda deve ser igual ao número de linhas na matriz à direita. Caso contrário, o operador × não será definido.

Identificarde matriz. Uma matriz de identidade, designada I, é uma matriz quadrada definida da seguinte maneira:

I*ij* = 1 se *i* = *j*, ou 0 de outra forma.

Em outras palavras, uma matriz de identidade contém 1 para cada elemento em que o número da linha é igual ao número da coluna e zero para todos os outros elementos. Por exemplo, aqui está a matriz de identidade 3 × 3.

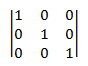
As igualdades a seguir são retensadas para qualquer matriz M.

M x I = M I x M = M

Transformações de Affine

Um de transformação de afim é uma operação matemática que mapeia um espaço de coordenadas para outro. Em outras palavras, ele mapeia um conjunto de pontos para outro conjunto de pontos. As transformações de Affine têm alguns recursos que os tornam úteis em elementos gráficos computacionais.

• As transformações de Affine preservam de collinearidade. Se três ou mais pontos cairem em uma linha, eles ainda formarão uma linha após a transformação. Linhas retas permanecem retas.
• A composição de duas transformações de affine é uma transformação affine.

As transformações de Affine para o espaço 2D têm o formulário a seguir.

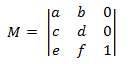
Se você aplicar a definição de multiplicação de matriz fornecida anteriormente, poderá mostrar que o produto de duas transformações de afins é outra transformação de afim. Para transformar um ponto 2D usando uma transformação de affine, o ponto é representado como uma matriz 1 × 3.

P = \| x y 1 \|

Os dois primeiros elementos contêm as coordenadas x e y do ponto. O 1 é colocado no terceiro elemento para fazer a matemática funcionar corretamente. Para aplicar a transformação, multiplique as duas matrizes da seguinte maneira.

P' = P × M

Isso se expande para o seguinte.

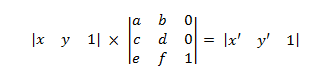
onde

x' = ax + cy + e y' = bx + dy + f

Para obter o ponto transformado, use os dois primeiros elementos da matriz P'.

p = (x', y') = (ax + cy + e, bx + dy + f)

Nota

Uma matriz de 1 × n é chamada de de vetor de linha. Direct2D e Direct3D usam vetores de linha para representar pontos em espaço 2D ou 3D. Você pode obter um resultado equivalente usando um vetor de coluna (n × 1) e transpondo a matriz de transformação. A maioria dos textos gráficos usa o formulário de vetor de coluna. Este tópico apresenta o formulário de vetor de linha para consistência com Direct2D e Direct3D.

 

As próximas seções derivam as transformações básicas.

Transformação de tradução

A matriz de transformação de tradução tem o formulário a seguir.

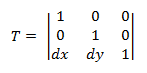
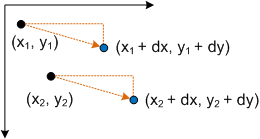
A conexão de um ponto P nesta equação gera:

P' = (*x* + *dx*, *y* + *dy*)

que corresponde ao ponto (x, y) traduzido por dx no eixo X e dy no eixo Y.

Transformação de dimensionamento

A matriz de transformação de dimensionamento tem o formulário a seguir.

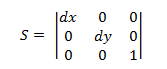
A conexão de um ponto P nesta equação gera:

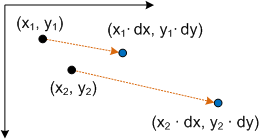
P' = (*x* ∙ *dx*, *y* ∙ *dy*)

que corresponde ao ponto (x,y) dimensionado por dx e dy.

Rotação ao redor da origem

A matriz para girar um ponto ao redor da origem tem o formulário a seguir.

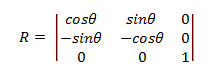
O ponto transformado é:

P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)

Prova. Para mostrar que P' representa uma rotação, considere o diagrama a seguir.

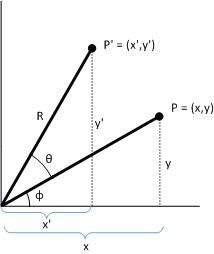
Dado:

P = (x,y)

O ponto original a ser transformado.

Φ

O ângulo formado pela linha (0,0) a P.

Θ

O ângulo pelo qual girar (x,y) sobre a origem.

P' = (x', y')

O ponto transformado.

R

O comprimento da linha (0,0) a P. Além disso, o raio do círculo de rotação.

Nota

Este diagrama usa o sistema de coordenadas padrão usado na geometria, em que o eixo y positivo aponta para cima. O Direct2D usa o sistema de coordenadas do Windows, em que o eixo y positivo aponta para baixo.

 

O ângulo entre o eixo x e a linha (0,0) a P' é Φ + Θ. As seguintes identidades contêm:

x = R cosΦ y = R sinΦ x' = R cos(Φ + Θ) y' = R sin(Φ+ Θ)

Agora resolva para x' e y' em termos de Θ. Pelas fórmulas de adição trigonométrica:

x' = R(cosΦcosΘ – sinΦsinΘ) = RcosΦcosΘ – RsinΦsinΘ 1 ' = R(sinΦcosΘ + cosΦsinΘ) = RsinΦcosΘ + RcosΦsinΘ

Substituindo, obtemos:

x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ

que corresponde ao ponto transformado P' mostrado anteriormente.

Rotação em torno de um ponto arbitrário

Para girar em torno de um ponto (x,y) diferente da origem, a matriz a seguir é usada.

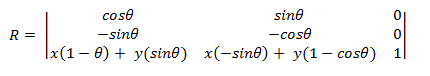
Você pode derivar essa matriz tomando o ponto (x,y) para ser a origem.

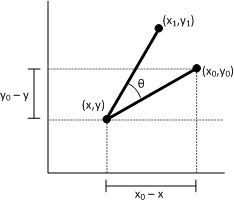
Let (x1, y1) be the point that resulting from rotating the point (x0, y0) around the point (x,y). Podemos derivar x1 da seguinte maneira.

x1 = (x0 – x)cosΘ– (y0 – y)sinΘ + x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]

Agora conecte essa equação de volta à matriz de transformação, usando a fórmula x1 = ax0 + cy0 + e de antes. Use o mesmo procedimento para derivar y1.

Transformação de distorção

A transformação de distorção é definida por quatro parâmetros:

• Θ: a quantidade a ser distorcida ao longo do eixo x, medida como um ângulo do eixo y.
• Φ: a quantidade a ser distorcida ao longo do eixo y, medida como um ângulo do eixo x.
• (px, py): as coordenadas x e y do ponto sobre o qual a distorção é executada.

A transformação de distorção usa a matriz a seguir.

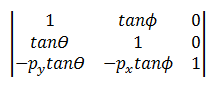
O ponto transformado é:

P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΦ) – *py*tanΦ

ou equivalentemente:

P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΦ)

Para ver como essa transformação funciona, considere cada componente individualmente. O parâmetro Θ move cada ponto na direção x por uma quantidade igual a tanΘ. O diagrama a seguir mostra a relação entre Θ e a distorção do eixo x.

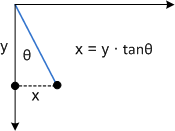
Aqui está a mesma distorção aplicada a um retângulo:

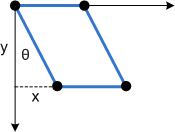
O parâmetro Φ tem o mesmo efeito, mas ao longo do eixo y:

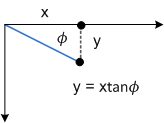
O próximo diagrama mostra a distorção do eixo y aplicada a um retângulo.

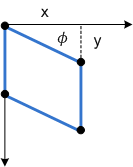
Por fim, os parâmetros px e py deslocar o ponto central para a distorção ao longo dos eixos x e y.

Representando transformações no Direct2D

Todas as transformações do Direct2D são transformações de afins. O Direct2D não dá suporte a transformações não afim. As transformações são representadas pela estrutura D2D1_MATRIX_3X2_F. Essa estrutura define uma matriz de 3 × 2. Como a terceira coluna de uma transformação de afins é sempre a mesma ([0, 0, 1]) e, como o Direct2D não dá suporte a transformações não afim, não é necessário especificar a matriz 3 × 3 inteira. Internamente, o Direct2D usa 3 matrizes × 3 para calcular as transformações.

Os membros do D2D1_MATRIX_3X2_F são nomeados de acordo com sua posição de índice: o membro _11 é o elemento (1,1), o membro _12 é o elemento (1,2) e assim por diante. Embora você possa inicializar os membros da estrutura diretamente, é recomendável usar a classe D2D1::Matrix3x2F. Essa classe herda D2D1_MATRIX_3X2_F e fornece métodos auxiliares para criar qualquer uma das transformações básicas de affine. A classe também definede operador de*() para compor duas ou mais transformações, conforme descrito em Aplicando Transformações no Direct2D.

Próximo

Módulo 4. Entrada do usuário