Diferentes maneiras de executar o Estimador de Recursos
Neste artigo, você aprenderá a trabalhar com o Azure Quantum Resource Estimator. O Resource Estimator faz parte do Quantum Development Kit e está disponível em diferentes plataformas e IDEs.
Se você executar um programa Q#, o Resource Estimator estará disponível no Visual Studio Code com a extensão Quantum Development Kit. Você não precisa ter uma assinatura do Azure para usar o Estimador de Recursos no Visual Studio Code.
Se você executar um programa Qiskit ou QIR, o Estimador de Recursos estará disponível no portal do Azure e você precisará de uma assinatura do Azure para usá-lo.
A tabela a seguir mostra as diferentes maneiras de executar o Estimador de Recursos.
| Cenário do usuário | Plataforma | Tutorial |
|---|---|---|
| Estimar os recursos de um programa Q# | Visual Studio Code | Selecione Q# no VS Code na parte superior da página |
| Estimar os recursos de um programa Q# (avançado) | Jupyter Notebook no Visual Studio Code | Selecione Q# no Jupyter Notebook na parte superior da página |
| Estimar os recursos de um programa Qiskit | Portal do Azure | Selecione Qiskit no portal do Azure na parte superior da página |
| Estimar os recursos de um programa QIR | Portal do Azure | Submeter QIR |
| Usar arquivos FCIDUMP como parâmetros de argumento (avançado) | Visual Studio Code | Enviar um problema de química quântica |
Pré-requisitos para o VS Code
- A versão mais recente do Visual Studio Code ou abra o VS Code na Web.
- A versão mais recente da extensão do Azure Quantum Development Kit. Para obter detalhes da instalação, consulte Instalando o QDK no VS Code.
Gorjeta
Você não precisa ter uma conta do Azure para executar o Estimador de Recursos local.
Criar um novo arquivo Q#
- Abra o Visual Studio Code e selecione File > New Text File para criar um novo arquivo.
- Guarde o ficheiro como
ShorRE.qs. Este ficheiro irá conter o código Q# para o seu programa.
Criar o algoritmo quântico
Copie o seguinte código para o ShorRE.qs arquivo:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
set nZeroes += 1;
set copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Executar o Estimador de Recursos
O Resource Estimator oferece seis parâmetros de qubit predefinidos, quatro dos quais têm conjuntos de instruções baseados em porta e dois que têm um conjunto de instruções Majorana. Ele também oferece dois códigos quânticos de correção de erros e surface_codefloquet_code.
Neste exemplo, você executa o Resource Estimator usando o qubit_gate_us_e3 parâmetro qubit e o código de correção de surface_code erro quântico.
Selecione Exibir -> Paleta de Comandos e digite "recurso", que deve exibir a opção Q#: Calcular Estimativas de Recursos . Você também pode clicar em Estimar na lista de comandos exibidos antes da
Mainoperação. Selecione esta opção para abrir a janela Estimador de Recursos.
Você pode selecionar um ou mais tipos de código de parâmetro Qubit + Correção de Erros para estimar os recursos. Para este exemplo, selecione qubit_gate_us_e3 e clique em OK.

Especifique o orçamento de erro ou aceite o valor padrão 0,001. Neste exemplo, deixe o valor padrão e pressione Enter.
Pressione Enter para aceitar o nome do resultado padrão com base no nome do arquivo, neste caso, ShorRE.
Ver os resultados
O Estimador de Recursos fornece várias estimativas para o mesmo algoritmo, cada uma mostrando compensações entre o número de qubits e o tempo de execução. Compreender a compensação entre tempo de execução e escala do sistema é um dos aspetos mais importantes da estimativa de recursos.
O resultado da estimativa de recursos é exibido na janela Estimativa Q#.
A guia Resultados exibe um resumo da estimativa de recursos. Clique no ícone ao lado da primeira linha para selecionar as colunas que deseja exibir. Você pode selecionar entre nome de execução, tipo de estimativa, tipo de qubit, esquema qec, orçamento de erro, qubits lógicos, profundidade lógica, distância de código, estados T, fábricas T, fração de fábrica T, tempo de execução, rQOPS e qubits físicos.

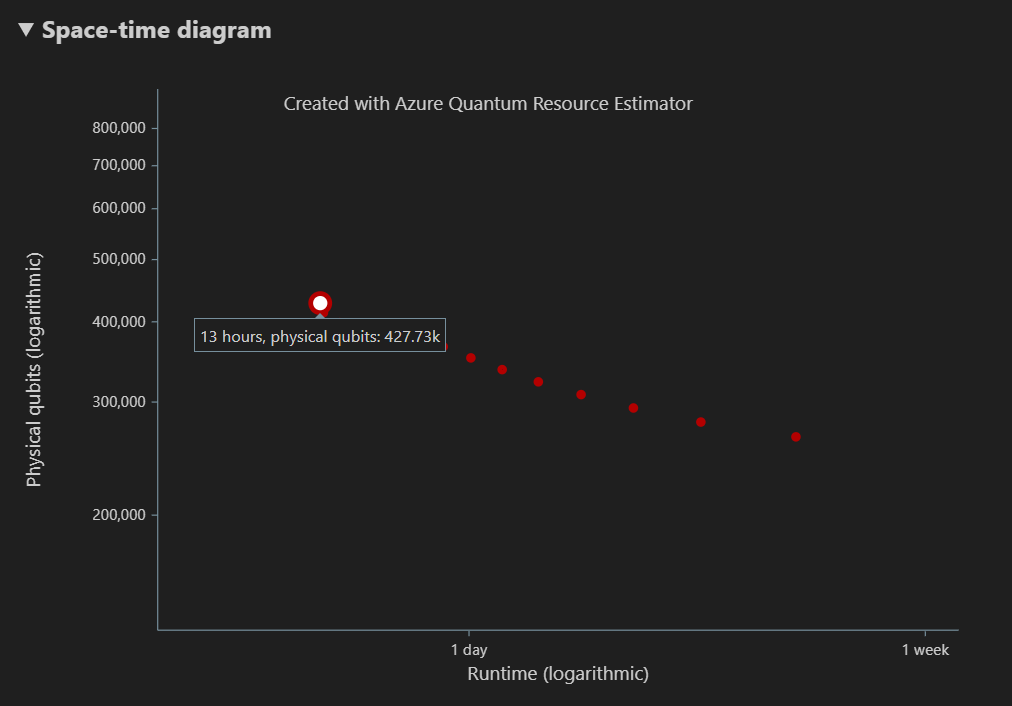
Na coluna Tipo de estimativa da tabela de resultados, você pode ver o número de combinações ideais de {número de qubits, tempo de execução} para seu algoritmo. Estas combinações podem ser vistas no diagrama espaço-temporal.
O diagrama espaço-tempo mostra as compensações entre o número de qubits físicos e o tempo de execução do algoritmo. Neste caso, o Estimador de Recursos encontra 13 combinações ideais diferentes entre milhares possíveis. Você pode passar o mouse sobre cada ponto {número de qubits, tempo de execução} para ver os detalhes da estimativa de recursos nesse ponto.
Para obter mais informações, consulte Diagrama espaço-temporal.
Nota
Você precisa clicar em um ponto do diagrama espaço-temporal, ou seja, um par {número de qubits, tempo de execução}, para ver o diagrama de espaço e os detalhes da estimativa de recursos correspondente a esse ponto.
O diagrama de espaço mostra a distribuição de qubits físicos usados para o algoritmo e as fábricas T, correspondendo a um par {número de qubits, tempo de execução}. Por exemplo, se você selecionar o ponto mais à esquerda no diagrama espaço-temporal, o número de qubits físicos necessários para executar o algoritmo será 427726, 196686 dos quais são qubits de algoritmo e 231040 dos quais são qubits de fábrica T.
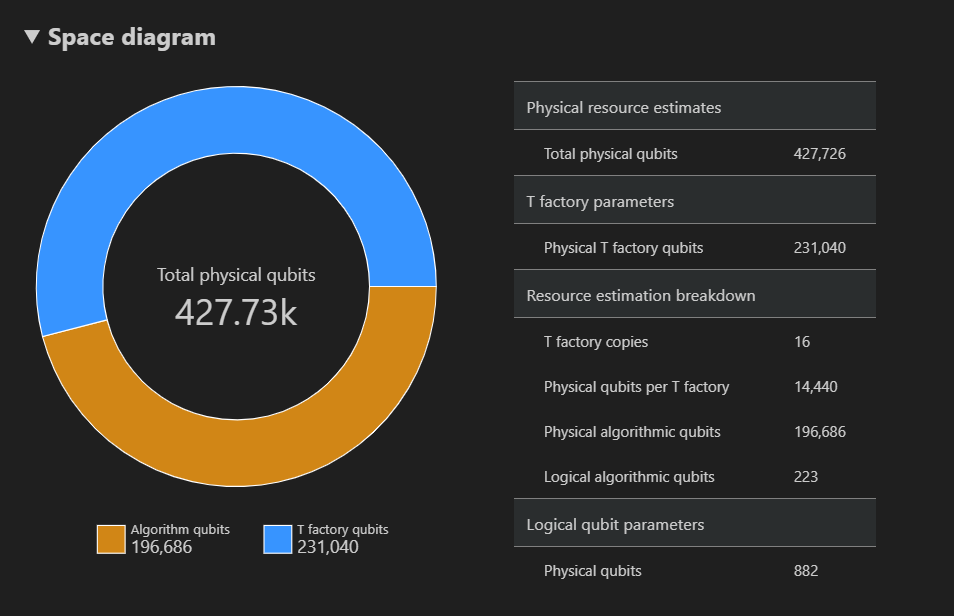
Finalmente, a guia Estimativas de Recursos exibe a lista completa de dados de saída para o Estimador de Recursos correspondente a um par {número de qubits, tempo de execução} . Você pode inspecionar os detalhes de custo recolhendo os grupos, que têm mais informações. Por exemplo, selecione o ponto mais à esquerda no diagrama espaço-tempo e recolha o grupo Parâmetros de qubit lógico.
Parâmetro qubit lógico Value Regime QEC surface_code Distância do código 21 Qubits físicos 882 Tempo de ciclo lógico 13 milissegundos Taxa de erro de qubit lógico 3,00E-13 Pré-fator de cruzamento 0.03 Limite de correção de erros 0,01 Fórmula de tempo de ciclo lógico (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceFórmula de qubits físicos 2 * codeDistance*codeDistanceGorjeta
Clique em Mostrar linhas detalhadas para exibir a descrição de cada saída dos dados do relatório.
Para obter mais informações, consulte os dados completos do relatório do Resource Estimator.
Alterar os target parâmetros
Você pode estimar o custo para o mesmo programa Q# usando outro tipo de qubit, código de correção de erro e orçamento de erro. Abra a janela Estimador de Recursos selecionando Exibir -> Paleta de Comandos e digite Q#: Calculate Resource Estimates.
Selecione qualquer outra configuração, por exemplo, o parâmetro qubit baseado em Majorana, qubit_maj_ns_e6. Aceite o valor de orçamento de erro padrão ou insira um novo e pressione Enter. O Resource Estimator executa novamente a estimativa com os novos target parâmetros.
Para obter mais informações, consulte Target parâmetros para o Estimador de Recursos.
Executar várias configurações de parâmetros
O Azure Quantum Resource Estimator pode executar várias configurações de parâmetros e comparar os resultados da estimativa de target recursos.
Selecione Exibir -> Paleta de Comandos ou pressione Ctrl+Shift+P e digite
Q#: Calculate Resource Estimates.Selecione qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code e qubit_maj_ns_e6 + floquet_code e clique em OK.
Aceite o valor de orçamento de erro padrão 0,001 e pressione Enter.
Pressione Enter para aceitar o arquivo de entrada, neste caso, ShorRE.qs.
No caso de várias configurações de parâmetros, os resultados são exibidos em linhas diferentes na guia Resultados .
O diagrama espaço-tempo mostra os resultados para todas as configurações de parâmetros. A primeira coluna da tabela de resultados exibe a legenda para cada configuração de parâmetros. Você pode passar o mouse sobre cada ponto para ver os detalhes da estimativa de recursos nesse ponto.
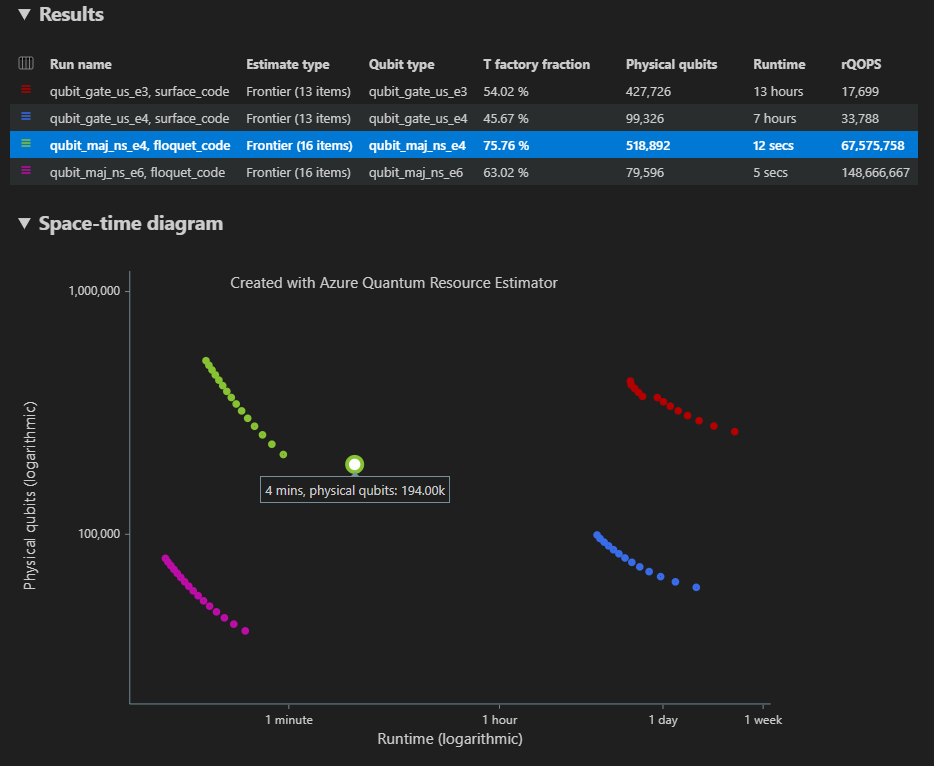
Clique em um ponto {número de qubits, tempo de execução} do diagrama espaço-tempo para exibir o diagrama de espaço correspondente e os dados do relatório.
Pré-requisitos para o Jupyter Notebook no VS Code
Um ambiente Python com Python e Pip instalados.
A versão mais recente do Visual Studio Code ou abra o VS Code na Web.
VS Code com as extensões Azure Quantum Development Kit, Python e Jupyter instaladas.
O Azure Quantum
qsharpeqsharp-widgetsos pacotes mais recentes.python -m pip install --upgrade qsharp qsharp-widgets
Gorjeta
Você não precisa ter uma conta do Azure para executar o Estimador de Recursos local.
Criar o algoritmo quântico
No VS Code, selecione View > Command palette e selecione Create: New Jupyter Notebook.
No canto superior direito, o VS Code detetará e exibirá a versão do Python e o ambiente Python virtual que foi selecionado para o notebook. Se você tiver vários ambientes Python, talvez seja necessário selecionar um kernel usando o seletor de kernel no canto superior direito. Se nenhum ambiente foi detetado, consulte Jupyter Notebooks no VS Code para obter informações de configuração.
Na primeira célula do bloco de anotações, importe o
qsharppacote.import qsharpAdicione uma nova célula e copie o código a seguir.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Estimar o algoritmo quântico
Agora, você estima os recursos físicos para a RunProgram operação usando as suposições padrão. Adicione uma nova célula e copie o código a seguir.
result = qsharp.estimate("RunProgram()")
result
A qsharp.estimate função cria um objeto de resultado, que pode ser usado para exibir uma tabela com as contagens gerais de recursos físicos. Você pode inspecionar os detalhes de custo recolhendo os grupos, que têm mais informações. Para obter mais informações, consulte os dados completos do relatório do Resource Estimator.
Por exemplo, feche o grupo de parâmetros de qubit lógico para ver se a distância do código é 21 e o número de qubits físicos é 882.
| Parâmetro qubit lógico | Value |
|---|---|
| Regime QEC | surface_code |
| Distância do código | 21 |
| Qubits físicos | 882 |
| Tempo de ciclo lógico | 8 milissegundos |
| Taxa de erro de qubit lógico | 3,00E-13 |
| Pré-fator de cruzamento | 0.03 |
| Limite de correção de erros | 0,01 |
| Fórmula de tempo de ciclo lógico | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Fórmula de qubits físicos | 2 * codeDistance * codeDistance |
Gorjeta
Para uma versão mais compacta da tabela de saída, você pode usar result.summaryo .
Diagrama de espaços
A distribuição de qubits físicos usados para o algoritmo e as fábricas T é um fator que pode afetar o design do seu algoritmo. Você pode usar o qsharp-widgets pacote para visualizar essa distribuição para entender melhor os requisitos de espaço estimados para o algoritmo.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
Neste exemplo, o número de qubits físicos necessários para executar o algoritmo são 829766, 196686 dos quais são qubits de algoritmo e 633080 dos quais são qubits de fábrica T.

Alterar os valores padrão e estimar o algoritmo
Ao enviar uma solicitação de estimativa de recursos para seu programa, você pode especificar alguns parâmetros opcionais. Use o jobParams campo para acessar todos os target parâmetros que podem ser passados para a execução do trabalho e ver quais valores padrão foram assumidos:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Você pode ver que o Resource Estimator usa o modelo de qubit, o código de correção de erro e o qubit_gate_ns_e3 surface_code orçamento de erro 0,001 como valores padrão para a estimativa.
Estes são os target parâmetros que podem ser personalizados:
errorBudget- o orçamento de erro global permitido para o algoritmoqecScheme- o esquema de correção de erros quânticos (QEC)qubitParams- os parâmetros físicos do qubitconstraints- as restrições ao nível dos componentesdistillationUnitSpecifications- as especificações para os algoritmos de destilação das fábricas TestimateType- única ou fronteiriça
Para obter mais informações, consulte Target parâmetros para o Estimador de Recursos.
Alterar modelo de qubit
Você pode estimar o custo para o mesmo algoritmo usando o parâmetro qubit baseado em Majorana, qubitParams, "qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Alterar o esquema de correção de erros quânticos
Você pode executar novamente o trabalho de estimativa de recursos para o mesmo exemplo nos parâmetros de qubit baseados em Majorana com um esquema QEC floqueado, qecScheme.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Alterar orçamento de erro
Em seguida, execute novamente o mesmo circuito quântico com um errorBudget de 10%.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Envio em lote com o Resource Estimator
O Azure Quantum Resource Estimator permite executar várias configurações de target parâmetros e comparar os resultados. Isso é útil quando você deseja comparar o custo de diferentes modelos de qubit, esquemas QEC ou orçamentos de erro.
Você pode executar uma estimativa em lote passando uma lista de target parâmetros para o
paramsqsharp.estimateparâmetro da função. Por exemplo, execute o mesmo algoritmo com os parâmetros padrão e os parâmetros de qubit baseados em Majorana com um esquema QEC de floquet.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Modelo Qubits lógicos Profundidade lógica Estados T Distância do código Fábricas T Fração de fábrica T Qubits físicos rQOPS Tempo de execução físico Baseado em portão, 10⁻³ 223 3.64 milh 4.70 milh 21 19 76.30 % 829,77 Milhares 26,55 milhões 31 segundos Majorana ns, 10⁻⁶ 223 3.64 milh 4.70 milh 5 19 63.02 % 79,60 mil 148.67 milh 5 segundos Você também pode construir uma lista de parâmetros de estimativa usando a
EstimatorParamsclasse.from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Modelo Qubits lógicos Profundidade lógica Estados T Distância do código Fábricas T Fração de fábrica T Qubits físicos rQOPS Tempo de execução físico μs baseados em portão, 10⁻³ 223 3,64 milhões 4.70 milh 17 13 40.54 % 216,77 Milhares 21,86 K 10 horas μs baseados em portão, 10⁻⁴ 223 3.64 milh 4.70 milh 9 14 43.17 % 63,57 Milhares 41,30 K 5 horas Baseado em portão, 10⁻³ 223 3,64 milhões 4.70 milh 17 16 69.08 % 416,89 Milhares 32.79 milh 25 segundos NS baseado em portão, 10⁻⁴ 223 3,64 milhões 4.70 milh 9 14 43.17 % 63,57 Milhares 61,94 milh 13 segundos Majorana ns, 10⁻⁴ 223 3,64 milhões 4.70 milh 9 19 82.75 % 501,48 K 82.59 milh 10 segundos Majorana ns, 10⁻⁶ 223 3,64 milhões 4.70 milh 5 13 31.47 % 42,96 Milhares 148.67 milh 5 segundos
Executando a estimativa da fronteira de Pareto
Ao estimar os recursos de um algoritmo, é importante considerar a compensação entre o número de qubits físicos e o tempo de execução do algoritmo. Você pode considerar a alocação do maior número possível de qubits físicos para reduzir o tempo de execução do algoritmo. No entanto, o número de qubits físicos é limitado pelo número de qubits físicos disponíveis no hardware quântico.
A estimativa de fronteira de Pareto fornece várias estimativas para o mesmo algoritmo, cada uma com uma compensação entre o número de qubits e o tempo de execução.
Para executar o Estimador de Recursos usando a estimativa de fronteira de Pareto, você precisa especificar o
"estimateType"target parâmetro como"frontier". Por exemplo, execute o mesmo algoritmo com os parâmetros de qubit baseados em Majorana com um código de superfície usando a estimativa de fronteira de Pareto.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Você pode usar a
EstimatesOverviewfunção para exibir uma tabela com as contagens gerais de recursos físicos. Clique no ícone ao lado da primeira linha para selecionar as colunas que deseja exibir. Você pode selecionar entre nome de execução, tipo de estimativa, tipo de qubit, esquema qec, orçamento de erro, qubits lógicos, profundidade lógica, distância de código, estados T, fábricas T, fração de fábrica T, tempo de execução, rQOPS e qubits físicos.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
Na coluna Tipo de estimativa da tabela de resultados, você pode ver o número de combinações diferentes de {número de qubits, tempo de execução} para seu algoritmo. Neste caso, o Estimador de Recursos encontra 22 combinações ótimas diferentes entre muitos milhares possíveis.
Diagrama espaço-tempo
A EstimatesOverview função também exibe o diagrama espaço-tempo do Estimador de Recursos.
O diagrama espaço-tempo mostra o número de qubits físicos e o tempo de execução do algoritmo para cada par {número de qubits, tempo de execução}. Você pode passar o mouse sobre cada ponto para ver os detalhes da estimativa de recursos nesse ponto.

Loteamento com estimativa de fronteira de Pareto
Para estimar e comparar várias configurações de parâmetros com estimativa de target fronteira, adicione
"estimateType": "frontier",aos parâmetros.result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])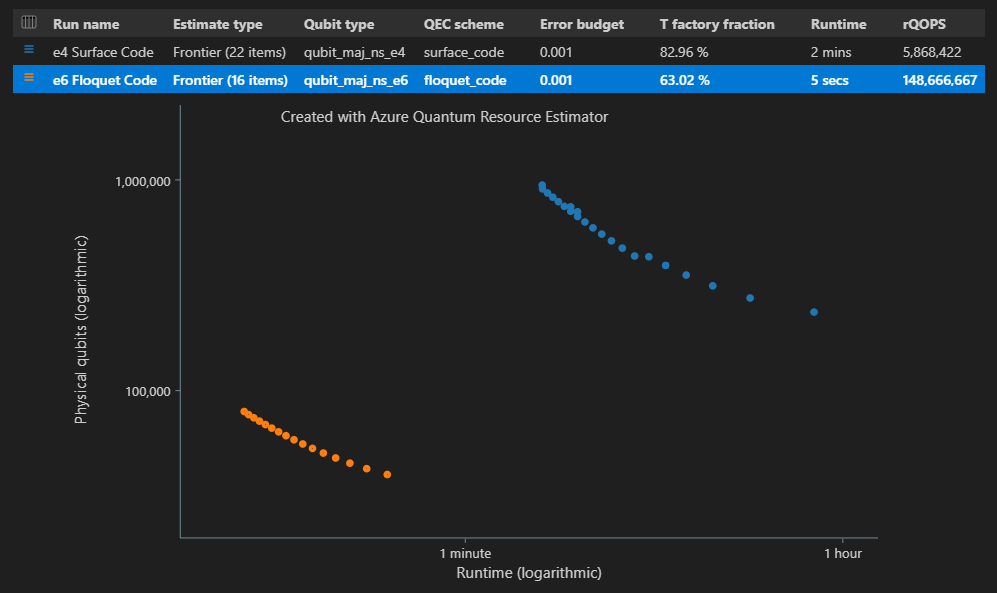
Nota
Você pode definir cores e executar nomes para o diagrama de tempo de qubit usando a
EstimatesOverviewfunção.Ao executar várias configurações de parâmetros usando a estimativa de fronteira de Pareto, você pode ver as estimativas de target recursos para um ponto específico do diagrama espaço-temporal, ou seja, para cada par {número de qubits, tempo de execução}. Por exemplo, o código a seguir mostra o uso de detalhes de estimativa para a segunda execução (índice de estimativa=0) e a quarta (índice de ponto=3) de tempo de execução mais curto.
EstimateDetails(result[1], 4)Você também pode ver o diagrama de espaço para um ponto específico do diagrama espaço-temporal. Por exemplo, o código a seguir mostra o diagrama de espaço para a primeira execução de combinações (índice de estimativa = 0) e o terceiro tempo de execução mais curto (índice de ponto = 2).
SpaceChart(result[0], 2)
Pré-requisitos para o Qiskit
- Uma conta do Azure com uma subscrição ativa. Se não tiver uma conta do Azure, registe-se gratuitamente e inscreva-se numa subscrição pré-paga.
- Um espaço de trabalho do Azure Quantum. Para obter mais informações, consulte Criar um espaço de trabalho do Azure Quantum.
Habilite o Azure Quantum Resource Estimator target em seu espaço de trabalho
O Resource Estimator é um target dos provedores de computação quântica da Microsoft. Se você criou um espaço de trabalho desde o lançamento do Resource Estimator, o provedor Microsoft Quantum Computing foi adicionado ao seu espaço de trabalho automaticamente.
Se você estiver usando um espaço de trabalho existente do Azure Quantum:
- Abra seu espaço de trabalho no portal do Azure.
- No painel esquerdo, em Operações, selecione Provedores.
- Selecione + Adicionar um provedor.
- Selecione + Adicionar para Microsoft Quantum Computing.
- Selecione Aprender & Desenvolver e selecione Adicionar.
Criar um novo bloco de notas na sua área de trabalho
- Faça logon no portal do Azure e selecione seu espaço de trabalho do Azure Quantum.
- Em Operações, selecione Blocos de Anotações
- Clique em Meus blocos de anotações e clique em Adicionar Novo
- Em Tipo de kernel, selecione IPython.
- Digite um nome para o arquivo e clique em Criar arquivo.
Quando o novo bloco de notas é aberto, cria automaticamente o código para a primeira célula, com base na sua subscrição e nas informações da área de trabalho.
from azure.quantum import Workspace
workspace = Workspace (
resource_id = "", # Your resource_id
location = "" # Your workspace location (for example, "westus")
)
Nota
Salvo indicação em contrário, deve executar cada célula em ordem à medida que a cria para evitar quaisquer problemas de compilação.
Clique no ícone triangular "play" à esquerda da célula para executar o código.
Carregue as importações necessárias
Primeiro, você precisará importar módulos adicionais do azure-quantum e qiskitdo .
Clique em + Código para adicionar uma nova célula e, em seguida, adicione e execute o seguinte código:
from azure.quantum.qiskit import AzureQuantumProvider
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import RGQFTMultiplier
Conectar-se ao serviço Azure Quantum
Em seguida, crie um objeto AzureQuantumProvider usando o workspace objeto da célula anterior para se conectar ao seu espaço de trabalho do Azure Quantum. Você cria uma instância de back-end e define o Resource Estimator como seu targetarquivo .
provider = AzureQuantumProvider(workspace)
backend = provider.get_backend('microsoft.estimator')
Criar o algoritmo quântico
Neste exemplo, você cria um circuito quântico para um multiplicador com base na construção apresentada em Ruiz-Perez e Garcia-Escartin (arXiv:1411.5949) que usa a Transformada Quântica de Fourier para implementar a aritmética.
Você pode ajustar o tamanho do multiplicador alterando a bitwidth variável. A geração do circuito é envolvida em uma função que pode ser chamada com o bitwidth valor do multiplicador. A operação terá dois registradores de entrada, cada um do tamanho do especificado bitwidth, e um registro de saída que é o dobro do tamanho do especificado bitwidth. A função também imprimirá algumas contagens de recursos lógicos para o multiplicador extraído diretamente do circuito quântico.
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
# Print a warning for large bitwidths that will require some time to generate and
# transpile the circuit.
if bitwidth > 18:
print(f"[WARN] It will take more than one minute generate a quantum circuit with a bitwidth larger than 18")
circ = RGQFTMultiplier(num_state_qubits=bitwidth, num_result_qubits=2 * bitwidth)
# One could further reduce the resource estimates by increasing the optimization_level,
# however, this will also increase the runtime to construct the algorithm. Note, that
# it does not affect the runtime for resource estimation.
print(f"[INFO] Decompose circuit into intrinsic quantum operations")
circ = transpile(circ, basis_gates=SUPPORTED_INSTRUCTIONS, optimization_level=0)
# print some statistics
print(f"[INFO] qubit count: {circ.num_qubits}")
print("[INFO] gate counts")
for gate, count in circ.count_ops().items():
print(f"[INFO] - {gate}: {count}")
return circ
Nota
Você pode enviar trabalhos de estimativa de recursos físicos para algoritmos que não têm estados T, mas que têm pelo menos uma medição.
Estimar o algoritmo quântico
Crie uma instância do seu algoritmo usando a create_algorithm função. Você pode ajustar o tamanho do multiplicador alterando a bitwidth variável.
bitwidth = 4
circ = create_algorithm(bitwidth)
Estime os recursos físicos para esta operação usando as suposições padrão. Você pode enviar o circuito para o back-end do Resource Estimator usando o run método e, em seguida, executar job.result() para aguardar a conclusão do trabalho e retornar os resultados.
job = backend.run(circ)
result = job.result()
result
Isso cria uma tabela que mostra as contagens gerais de recursos físicos. Você pode inspecionar os detalhes de custo recolhendo os grupos, que têm mais informações.
Gorjeta
Para uma versão mais compacta da tabela de saída, você pode usar result.summaryo .
Por exemplo, se você recolher o grupo de parâmetros de qubit lógico, poderá ver mais facilmente que a distância do código de correção de erro é 15.
| Parâmetro qubit lógico | Value |
|---|---|
| Regime QEC | surface_code |
| Distância do código | 15 |
| Qubits físicos | 450 |
| Tempo de ciclo lógico | 6º |
| Taxa de erro de qubit lógico | 3,00E-10 |
| Pré-fator de cruzamento | 0.03 |
| Limite de correção de erros | 0,01 |
| Fórmula de tempo de ciclo lógico | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Fórmula de qubits físicos | 2 * codeDistance * codeDistance |
No grupo Parâmetros de qubit físico, você pode ver as propriedades de qubit físico que foram assumidas para essa estimativa. Por exemplo, o tempo para executar uma medição de qubit único e uma porta de qubit único são assumidos como 100 ns e 50 ns, respectivamente.
Gorjeta
Você também pode acessar a saída do Resource Estimator como um dicionário Python usando o método result.data().
Para obter mais informações, consulte a lista completa de dados de saída para o Resource Estimator.
Diagramas de espaço
A distribuição de qubits físicos usados para o algoritmo e as fábricas T é um fator que pode afetar o design do seu algoritmo. Você pode visualizar essa distribuição para entender melhor os requisitos de espaço estimados para o algoritmo.
result.diagram.space

O diagrama de espaço mostra a proporção de qubits de algoritmo e qubits de fábrica T. Observe que o número de cópias de fábrica T, 28, contribui para o número de qubits físicos para fábricas T como $\text{T factories} \cdot \text{physical qubit per T factory}= 28 \cdot 18.000 = 504.000$.
Para obter mais informações, consulte Estimativa física de fábrica T.
Alterar os valores padrão e estimar o algoritmo
Ao enviar uma solicitação de estimativa de recursos para seu programa, você pode especificar alguns parâmetros opcionais. Use o jobParams campo para acessar todos os valores que podem ser passados para a execução do trabalho e ver quais valores padrão foram assumidos:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Estes são os target parâmetros que podem ser personalizados:
errorBudget- o orçamento global de erros permitidosqecScheme- o esquema de correção de erros quânticos (QEC)qubitParams- os parâmetros físicos do qubitconstraints- as restrições ao nível dos componentesdistillationUnitSpecifications- as especificações para os algoritmos de destilação das fábricas T
Para obter mais informações, consulte Target parâmetros para o Estimador de Recursos.
Alterar modelo de qubit
Em seguida, estime o custo para o mesmo algoritmo usando o parâmetro qubit baseado em Majorana qubit_maj_ns_e6
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
})
result = job.result()
result
Você pode inspecionar as contagens físicas programaticamente. Por exemplo, você pode explorar detalhes sobre a fábrica T que foi criada para executar o algoritmo.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Nota
Por padrão, o tempo de execução é mostrado em nanossegundos.
Você pode usar esses dados para produzir algumas explicações de como as fábricas T produzem os estados T necessários.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numModulesPerRound"][round]} {tfactory["moduleNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Alterar o esquema de correção de erros quânticos
Agora, execute novamente o trabalho de estimativa de recursos para o mesmo exemplo nos parâmetros de qubit baseados em Majorana com um esquema QEC floqued, qecScheme.
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
},
qecScheme={
"name": "floquet_code"
})
result_maj_floquet = job.result()
result_maj_floquet
Alterar orçamento de erro
Vamos executar novamente o mesmo circuito quântico com um errorBudget de 10%.
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
},
qecScheme={
"name": "floquet_code"
},
errorBudget=0.1)
result_maj_floquet_e1 = job.result()
result_maj_floquet_e1
Nota
Se tiver algum problema ao trabalhar com o Estimador de Recursos, consulte a página Resolução de problemas ou contacte AzureQuantumInfo@microsoft.com.