Regressão
Nota
Consulte a guia Texto e imagens para obter mais detalhes!
Os modelos de regressão são treinados para prever valores de rótulos numéricos com base em dados de treinamento que incluem recursos e rótulos conhecidos. O processo de treinamento de um modelo de regressão (ou de fato, qualquer modelo supervisionado de aprendizado de máquina) envolve várias iterações nas quais você usa um algoritmo apropriado (geralmente com algumas configurações parametrizadas) para treinar um modelo, avaliar o desempenho preditivo do modelo e refinar o modelo repetindo o processo de treinamento com diferentes algoritmos e parâmetros até atingir um nível aceitável de precisão preditiva.

O diagrama mostra quatro elementos-chave do processo de treinamento para modelos supervisionados de aprendizado de máquina:
- Divida os dados de treinamento (aleatoriamente) para criar um conjunto de dados com o qual treinar o modelo enquanto retém um subconjunto dos dados que você usará para validar o modelo treinado.
- Use um algoritmo para ajustar os dados de treinamento a um modelo. No caso de um modelo de regressão, use um algoritmo de regressão, como a regressão linear.
- Use os dados de validação que você reteve para testar o modelo prevendo rótulos para os recursos.
- Compare os rótulos reais conhecidos no conjunto de dados de validação com os rótulos que o modelo previu. Em seguida, agregue as diferenças entre os valores de rótulo previstos e reais para calcular uma métrica que indique com que precisão o modelo previu para os dados de validação.
Após cada treino, validação e avaliação da iteração, você pode repetir o processo com diferentes algoritmos e parâmetros até que uma métrica de avaliação aceitável seja alcançada.
Exemplo - regressão
Vamos explorar a regressão com um exemplo simplificado no qual treinaremos um modelo para prever um rótulo numérico (y) com base em um único valor de recurso (x). A maioria dos cenários reais envolve vários valores de recursos, o que adiciona alguma complexidade; Mas o princípio é o mesmo.
Para o nosso exemplo, vamos ficar com o cenário de vendas de sorvete que discutimos anteriormente. Para o nosso recurso, vamos considerar a temperatura (vamos supor que o valor é a temperatura máxima em um determinado dia), e o rótulo que queremos treinar um modelo para prever é o número de sorvetes vendidos naquele dia. Vamos começar com alguns dados históricos que incluem registros de temperaturas diárias (x) e vendas de sorvete (y):

|

|
|---|---|
| Temperatura (x) | Vendas de gelados (y) |
| 51 | 1 |
| 52 | 0 |
| 67 | 14 |
| 65 | 14 |
| 70 | 23 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| setenta e três | 22 |
| 81 | 30 |
| setenta e oito | 26 |
| 83 | 36 |
Treinando um modelo de regressão
Começaremos dividindo os dados e usando um subconjunto deles para treinar um modelo. Aqui está o conjunto de dados de treinamento:
| Temperatura (x) | Vendas de gelados (y) |
|---|---|
| 51 | 1 |
| 65 | 14 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 81 | 30 |
Para obter uma visão de como esses valores x e y podem se relacionar entre si, podemos plotá-los como coordenadas ao longo de dois eixos, assim:
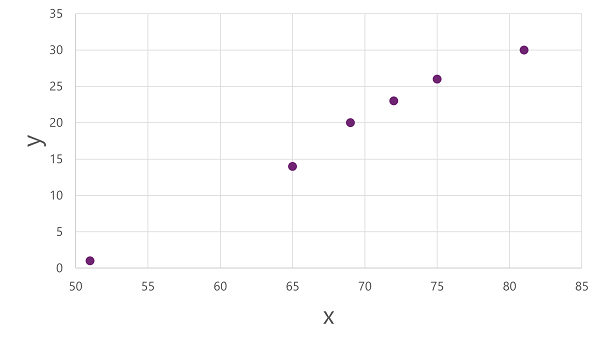
Agora estamos prontos para aplicar um algoritmo aos nossos dados de treinamento e ajustá-lo a uma função que aplica uma operação a x para calcular y. Um desses algoritmos é a regressão linear, que funciona derivando uma função que produz uma linha reta através das interseções dos valores x e y enquanto minimiza a distância média entre a linha e os pontos plotados, assim:

A linha é uma representação visual da função na qual a inclinação da linha descreve como calcular o valor de y para um determinado valor de x. A linha interceta o eixo x em 50, então quando x é 50, y é 0. Como você pode ver nos marcadores de eixo no gráfico, a linha inclina-se de modo que cada aumento de 5 ao longo do eixo x resulta em um aumento de 5 até o eixo y ; assim, quando x é 55, y é 5; quando x é 60, y é 10, e assim por diante. Para calcular um valor de y para um dado valor de x, a função simplesmente subtrai 50; Em outras palavras, a função pode ser expressa assim:
f(x) = x-50
Você pode usar essa função para prever o número de sorvetes vendidos em um dia com qualquer temperatura. Por exemplo, suponha que a previsão do tempo nos diga que amanhã serão 77 graus. Podemos aplicar nosso modelo para calcular 77-50 e prever que venderemos 27 sorvetes amanhã.
Mas quão preciso é o nosso modelo?
Avaliação de um modelo de regressão
Para validar o modelo e avaliar o quão bem ele prevê, retimos alguns dados para os quais sabemos o valor do rótulo (y). Aqui estão os dados que retimos:
| Temperatura (x) | Vendas de gelados (y) |
|---|---|
| 52 | 0 |
| 67 | 14 |
| 70 | 23 |
| setenta e três | 22 |
| setenta e oito | 26 |
| 83 | 36 |
Podemos usar o modelo para prever o rótulo para cada uma das observações neste conjunto de dados com base no valor do recurso (x); e, em seguida, compare o rótulo previsto (ŷ) com o valor real conhecido do rótulo (y).
Usando o modelo que treinamos anteriormente, que encapsula a função f(x) = x-50, resulta nas seguintes previsões:
| Temperatura (x) | Vendas efetivas (y) | Vendas previstas (ŷ) |
|---|---|---|
| 52 | 0 | 2 |
| 67 | 14 | 17 |
| 70 | 23 | 20 |
| setenta e três | 22 | 23 |
| setenta e oito | 26 | 28 |
| 83 | 36 | 33 |
Podemos plotar os rótulos previstos e reais em relação aos valores de recurso da seguinte forma:

Os rótulos previstos são calculados pelo modelo para que estejam na linha da função, mas há alguma variância entre os valores ŷ calculados pela função e os valores y reais do conjunto de dados de validação; que é indicado no gráfico como uma linha entre os valores ŷ e y que mostra o quão longe a previsão estava do valor real.
Métricas de avaliação de regressão
Com base nas diferenças entre os valores previstos e reais, você pode calcular algumas métricas comuns que são usadas para avaliar um modelo de regressão.
Erro Absoluto Médio (MAE)
A variância neste exemplo indica por quantos sorvetes cada previsão estava errada. Não importa se a previsão foi maior ou inferior ao valor real (assim, por exemplo, -3 e +3 indicam uma variância de 3). Essa métrica é conhecida como erro absoluto para cada previsão e pode ser resumida para todo o conjunto de validação como o erro absoluto médio (MAE).
No exemplo do sorvete, a média (média) dos erros absolutos (2, 3, 3, 1, 2 e 3) é de 2,33.
Erro quadrático médio (MSE)
A métrica de erro absoluto médio leva todas as discrepâncias entre rótulos previstos e reais igualmente em consideração. No entanto, pode ser mais desejável ter um modelo que esteja consistentemente errado por uma pequena quantidade do que um que cometa menos erros, mas maiores. Uma maneira de produzir uma métrica que "amplifica" erros maiores, quadrando os erros individuais e calculando a média dos valores quadrados. Essa métrica é conhecida como erro quadrático médio (MSE).
No nosso exemplo de sorvete, a média dos valores absolutos quadrados (que são 4, 9, 9, 1, 4 e 9) é 6.
Erro quadrático médio raiz (RMSE)
O erro quadrado médio ajuda a levar em conta a magnitude dos erros, mas como ele quadra os valores de erro, a métrica resultante não representa mais a quantidade medida pelo rótulo. Em outras palavras, podemos dizer que a MPE do nosso modelo é 6, mas isso não mede sua precisão em termos do número de sorvetes que foram mal previstos; 6 é apenas uma pontuação numérica que indica o nível de erro nas previsões de validação.
Se quisermos medir o erro em termos do número de gelados, temos de calcular a raiz quadrada da MPE; que produz uma métrica chamada, sem surpresa, Root Mean Squared Error. Neste caso √6, que é 2,45 (gelados).
Coeficiente de determinação (R2)
Todas as métricas até agora comparam a discrepância entre os valores previstos e reais para avaliar o modelo. No entanto, na realidade, há alguma variação aleatória natural nas vendas diárias de sorvete que o modelo leva em conta. Em um modelo de regressão linear, o algoritmo de treinamento se ajusta a uma linha reta que minimiza a variância média entre a função e os valores de rótulo conhecidos. O coeficiente de determinação (mais comumente referido como R2 ou R-quadrado) é uma métrica que mede a proporção de variância nos resultados de validação que pode ser explicada pelo modelo, em oposição a algum aspeto anômalo dos dados de validação (por exemplo, um dia com um número altamente incomum de vendas de sorvetes por causa de um festival local).
O cálculo para R2 é mais complexo do que para as métricas anteriores. Ele compara a soma das diferenças ao quadrado entre os rótulos previstos e reais com a soma das diferenças ao quadrado entre os valores reais do rótulo e a média dos valores reais do rótulo, da seguinte forma:
R2 = 1- ∑(y-ŷ)2 ÷ ∑(y-ȳ)2
Não se preocupe muito se isso parecer complicado; A maioria das ferramentas de aprendizado de máquina pode calcular a métrica para você. O ponto importante é que o resultado é um valor entre 0 e 1 que descreve a proporção de variância explicada pelo modelo. Em termos simples, quanto mais próximo de 1 for este valor, melhor o modelo está a ajustar os dados de validação. No caso do modelo de regressão de sorvete, o R2 calculado a partir dos dados de validação é de 0,95.
Formação iterativa
As métricas descritas acima são comumente usadas para avaliar um modelo de regressão. Na maioria dos cenários do mundo real, um cientista de dados usará um processo iterativo para treinar e avaliar repetidamente um modelo, variando:
- Seleção e preparação de recursos (escolha de quais recursos incluir no modelo e cálculos aplicados a eles para ajudar a garantir um melhor ajuste).
- Seleção de algoritmos (Exploramos a regressão linear no exemplo anterior, mas existem muitos outros algoritmos de regressão)
- Parâmetros do algoritmo (configurações numéricas para controlar o comportamento do algoritmo, mais precisamente chamados de hiperparâmetros para diferenciá-los dos parâmetros x e y ).
Após várias iterações, o modelo que resulta na melhor métrica de avaliação aceitável para o cenário específico é selecionado.