O que é a classificação?
A classificação binária é uma classificação com duas categorias. Por exemplo, poderíamos rotular os pacientes como não diabéticos ou diabéticos.
A previsão de classe é feita determinando a probabilidade para cada classe possível como um valor entre 0 (impossível) e 1 (certo). A probabilidade total para todas as classes é sempre 1, pois o paciente é definitivamente diabético ou não diabético. Assim, se a probabilidade prevista de um paciente ser diabético é de 0,3, então há uma probabilidade correspondente de 0,7 de que o paciente não é diabético.
Um valor limite, geralmente 0,5, é usado para determinar a classe prevista. Se a classe positiva (neste caso, diabético) tem uma probabilidade prevista maior do que o limiar, então uma classificação de diabético é prevista.
Formação e avaliação de um modelo de classificação
A classificação é um exemplo de uma técnica de aprendizado de máquina supervisionada, o que significa que ela depende de dados que incluem valores de recurso conhecidos e valores de rótulo conhecidos. Neste exemplo, os valores de recurso são medições diagnósticas para pacientes, e os valores do rótulo são uma classificação de não diabético ou diabético. Um algoritmo de classificação é usado para ajustar um subconjunto dos dados em uma função que pode calcular a probabilidade para cada rótulo de classe a partir dos valores do recurso. Os dados restantes são usados para avaliar o modelo, comparando as previsões que ele gera a partir dos recursos com os rótulos de classe conhecidos.
Um exemplo simples
Vamos explorar um exemplo para ajudar a explicar os princípios-chave. Suponhamos que temos os seguintes dados do paciente, que consistem em uma única característica (nível de glicose no sangue) e um rótulo de classe 0 para não diabéticos, 1 para diabéticos.
| Glicose no sangue | Diabéticos |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
Usamos as primeiras oito observações para treinar um modelo de classificação, e começamos traçando a característica de glicose no sangue (x) e o rótulo diabético previsto (y).
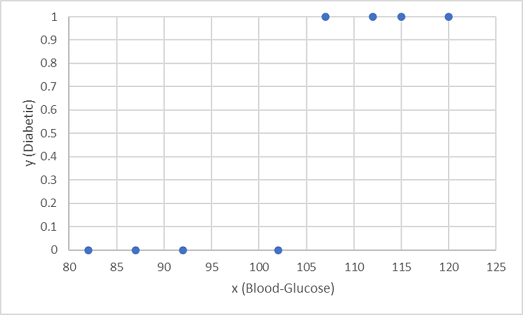
O que precisamos é de uma função que calcule um valor de probabilidade para y com base em x (em outras palavras, precisamos da função f(x) = y). Você pode ver no gráfico que os pacientes com um nível baixo de glicose no sangue são todos não-diabéticos, enquanto os pacientes com um nível mais alto de glicose no sangue são diabéticos. Parece que quanto maior o nível de glicose no sangue, mais provável é que um paciente seja diabético, com o ponto de inflexão sendo algo entre 100 e 110. Precisamos ajustar uma função que calcula um valor entre 0 e 1 para y a esses valores.
Uma dessas funções é uma função logística , que forma uma curva sigmoidal (em forma de S).
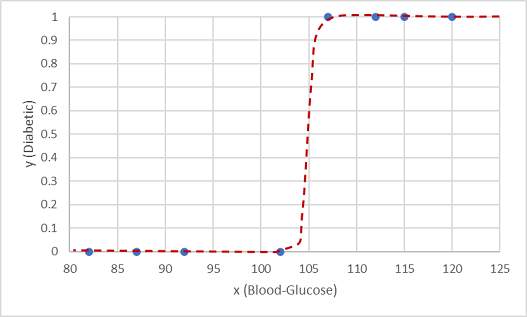
Agora podemos usar a função para calcular um valor de probabilidade de que y é positivo, o que significa que o paciente é diabético, a partir de qualquer valor de x, encontrando o ponto na linha de função para x. Podemos definir um valor limite de 0,5 como o ponto de corte para a previsão do rótulo da classe.
Vamos testá-lo com os dois valores de dados que retimos.
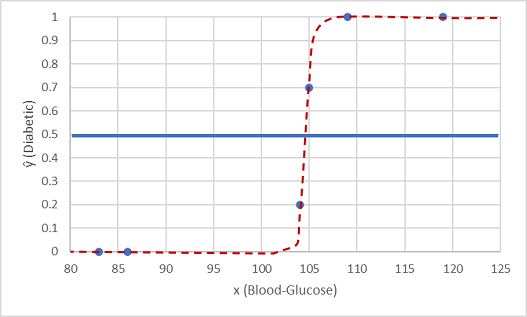
Os pontos plotados abaixo da linha limiar produzem uma classe prevista de 0 (não diabético) e os pontos acima da linha são previstos como 1 (diabético).
Agora podemos comparar as previsões de rótulos (ŷ, ou "y-hat"), com base na função logística encapsulada no modelo, com os rótulos de classe reais (y).
| x | S | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |