Различные способы запуска оценки ресурсов
В этой статье вы узнаете, как работать с оценщиком ресурсов Azure Quantum. Оценка ресурсов входит в состав комплекта средств разработки Quantum и доступна на разных платформах и средах разработки.
Если вы запускаете программу Q#, средство оценки ресурсов доступно в Visual Studio Code с расширением Quantum Development Kit. Подписка Azure не требуется использовать средство оценки ресурсов в Visual Studio Code.
Если вы запускаете программу Qiskit или QIR, средство оценки ресурсов доступно в портал Azure, и вам нужна подписка Azure для его использования.
В следующей таблице показаны различные способы запуска средства оценки ресурсов.
| Пользовательский сценарий | Платформа | Учебник |
|---|---|---|
| Оценка ресурсов программы Q# | Visual Studio Code | Выберите Q# в VS Code в верхней части страницы |
| Оценка ресурсов программы Q# (дополнительно) | Записная книжка Jupyter в Visual Studio Code | Выберите Q# в Jupyter Notebook в верхней части страницы |
| Оценка ресурсов программы Qiskit | Портал Azure | Выберите Qiskit в портал Azure в верхней части страницы |
| Оценка ресурсов программы QIR | Портал Azure | Отправка QIR |
| Использование файлов FCIDUMP в качестве параметров аргумента (дополнительно) | Visual Studio Code | Отправка проблемы квантовой химии |
Предварительные требования для VS Code
- Последняя версия Visual Studio Code или откройте VS Code в Интернете.
- Последняя версия расширения Пакета средств разработки Azure Quantum. Дополнительные сведения об установке см. в разделе "Установка QDK" в VS Code.
Совет
Для запуска локального оценщика ресурсов не требуется учетная запись Azure.
Создание файла Q#
- Откройте Visual Studio Code и выберите "Создать > текстовый файл ", чтобы создать новый файл.
- Сохраните файл как
ShorRE.qs. Этот файл будет содержать код Q# для программы.
Создание квантового алгоритма
Скопируйте в файл ShorRE.qs следующий код:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
set nZeroes += 1;
set copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Запуск средства оценки ресурсов
Оценка ресурсов предлагает шесть предопределенных параметров кубита, четыре из которых имеют наборы инструкций на основе шлюза и два с набором инструкций Majorana. Он также предлагает два кода исправления квантовых ошибок и surface_code floquet_code.
В этом примере вы запустите средство оценки ресурсов с помощью qubit_gate_us_e3 параметра кубита и surface_code кода исправления квантовых ошибок.
Выберите представление —> палитра команд и введите "ресурс", который должен открыть параметр Q#: Вычисление оценки ресурсов. Вы также можете щелкнуть "Оценка " в списке команд, отображаемых прямо перед операцией
Main. Выберите этот параметр, чтобы открыть окно оценки ресурсов.
Чтобы оценить ресурсы, можно выбрать один или несколько параметров Кубита + типы кода исправления ошибок. В этом примере выберите qubit_gate_us_e3 и нажмите кнопку "ОК".
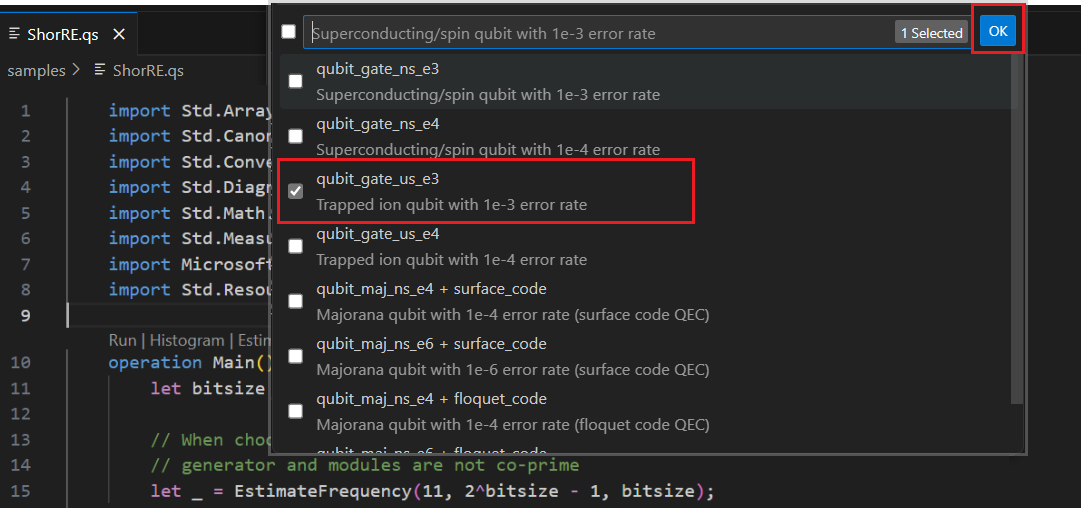
Укажите бюджет ошибки или примите значение по умолчанию 0,001. В этом примере оставьте значение по умолчанию и нажмите клавишу ВВОД.
Нажмите клавишу ВВОД , чтобы принять имя результата по умолчанию на основе имени файла, в данном случае ShorRE.
Просмотр результатов
Оценка ресурсов предоставляет несколько оценок для одного и того же алгоритма, каждый из которых показывает компромиссы между числом кубитов и средой выполнения. Понимание компромисса между средой выполнения и системным масштабированием является одним из более важных аспектов оценки ресурсов.
Результат оценки ресурсов отображается в окне оценки Q#.
На вкладке "Результаты " отображается сводка по оценке ресурсов. Щелкните значок рядом с первой строкой, чтобы выбрать столбцы, которые нужно отобразить. Вы можете выбрать имя запуска, оценить тип, тип кубита, схему qec, бюджет ошибок, логические кубиты, логическую глубину, расстояние кода, T состояния, фабрики T, дробь фабрики T, среду выполнения, rQOPS и физические кубиты.

В столбце "Оценка типа" таблицы результатов вы увидите количество оптимальных сочетаний {число кубитов, среда выполнения} для алгоритма. Эти сочетания можно увидеть на схеме пространства.
На схеме пробелов показаны компромиссы между количеством физических кубитов и средой выполнения алгоритма. В этом случае оценка ресурсов находит 13 различных оптимальных сочетаний из многих тысяч возможных. Вы можете навести указатель мыши на каждый {число кубитов, среда выполнения}, чтобы просмотреть сведения о оценке ресурсов на этом этапе.
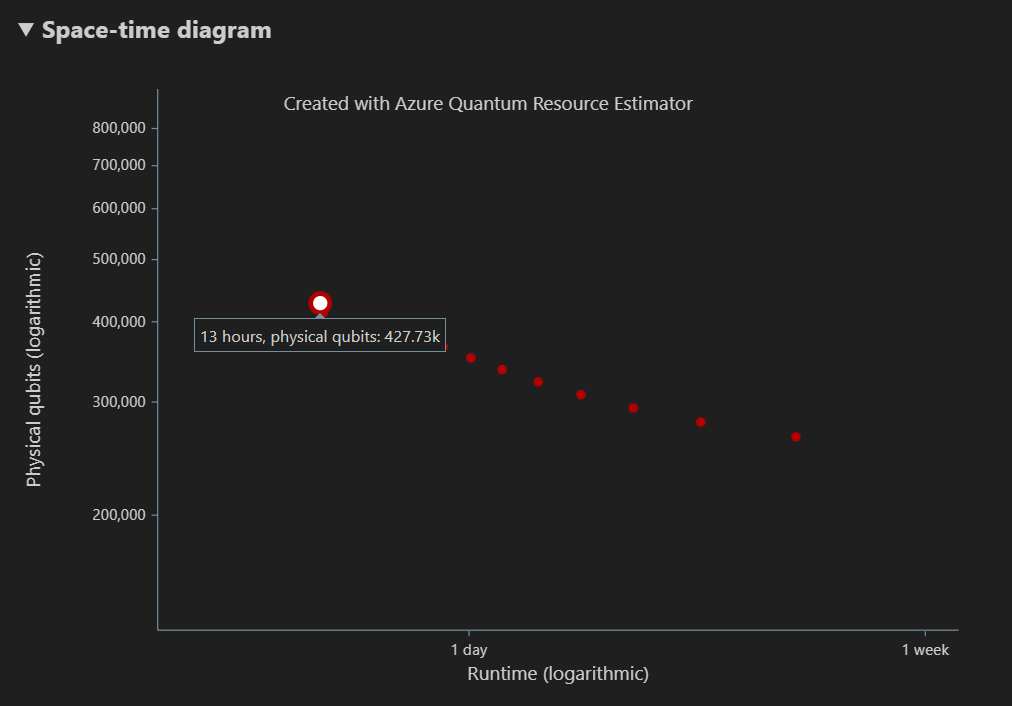
Дополнительные сведения см. на схеме пространства времени.
Примечание.
Чтобы просмотреть схему пространства, соответствующую этой точке, необходимо щелкнуть одну точку схемы пространства, то есть {количество кубитов, среды выполнения}, чтобы просмотреть схему пространства и сведения о оценке ресурсов, соответствующей этой точке.
Схема пространства показывает распределение физических кубитов, используемых для алгоритма и фабрик T, соответствующих паре {число кубитов, среда выполнения}. Например, если выбрать самую левую точку на схеме времени, количество физических кубитов, необходимых для выполнения алгоритма, 427726, 196686 из которых являются кубитами алгоритмов и 231040 из которых являются кубитами фабрики T.
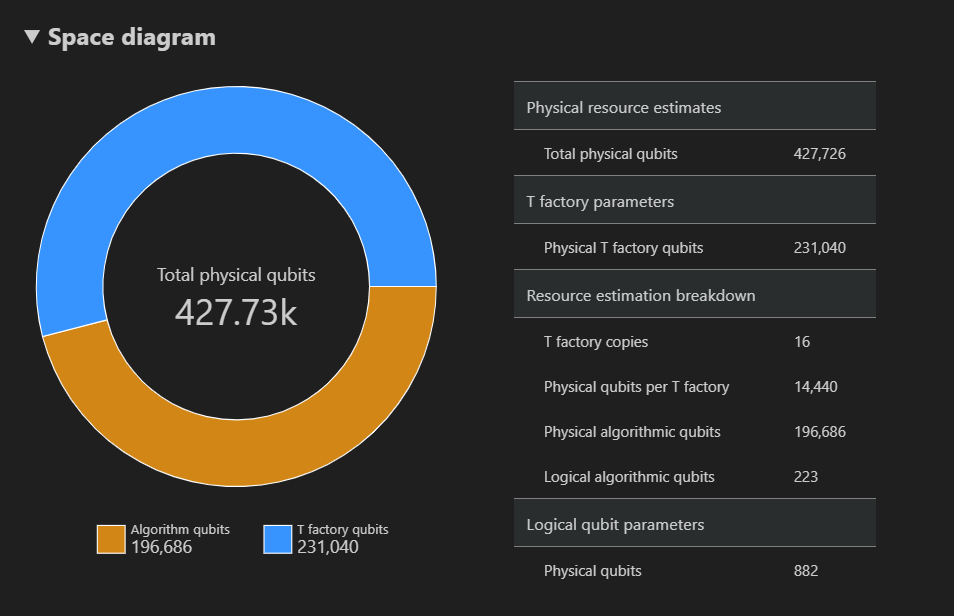
Наконец, на вкладке "Оценки ресурсов" отображается полный список выходных данных для средства оценки ресурсов, соответствующего {количеству кубитов, среде выполнения} пары. Вы можете проверить сведения о затратах, совершите группы, которые содержат дополнительные сведения. Например, выберите самую левую точку на схеме пространства и свернуть группу параметров логического кубита.
Логический параметр кубита Значение Схема QEC surface_code Расстояние от кода 21 Физические кубиты 882 Время логического цикла 13 миллисек Частота ошибок логического кубита 3.00E-13 Пересечение префактотора 0,03 Порог исправления ошибок 0,01 Формула логического цикла (4 * + twoQubitGateTime2 * ) *oneQubitMeasurementTimecodeDistanceФормула физических кубитов 2 * codeDistance*codeDistanceСовет
Нажмите кнопку "Показать подробные строки" , чтобы отобразить описание каждого вывода данных отчета.
Дополнительные сведения см . в полных отчетах о оценке ресурсов.
target Изменение параметров
Вы можете оценить стоимость той же программы Q# с помощью другого типа кубита, кода исправления ошибок и бюджета ошибок. Откройте окно оценки ресурсов, выбрав представление —> палитру команд и введите Q#: Calculate Resource Estimates.
Выберите любую другую конфигурацию, например параметр кубита на основе Майораны. qubit_maj_ns_e6 Примите значение бюджета ошибки по умолчанию или введите новую и нажмите клавишу ВВОД. Рестиматор ресурсов повторно запускает оценку с новыми target параметрами.
Дополнительные сведения см Target . в параметрах оценки ресурсов.
Запуск нескольких конфигураций параметров
Оценка ресурсов Azure Quantum может выполнять несколько конфигураций target параметров и сравнивать результаты оценки ресурсов.
Выберите представление —> палитра команд или нажмите клавиши CTRL+SHIFT+P и введите
Q#: Calculate Resource Estimates.Выберите qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code и qubit_maj_ns_e6 + floquet_code и нажмите кнопку "ОК".
Примите значение бюджета ошибки по умолчанию 0.001 и нажмите клавишу ВВОД.
Нажмите клавишу ВВОД , чтобы принять входной файл, в данном случае ShorRE.qs.
В случае нескольких конфигураций параметров результаты отображаются в разных строках на вкладке "Результаты ".
На схеме пространства отображаются результаты для всех конфигураций параметров. Первый столбец таблицы результатов отображает условные обозначения для каждой конфигурации параметров. Вы можете навести указатель мыши на каждую точку, чтобы просмотреть сведения о оценке ресурсов на этом этапе.
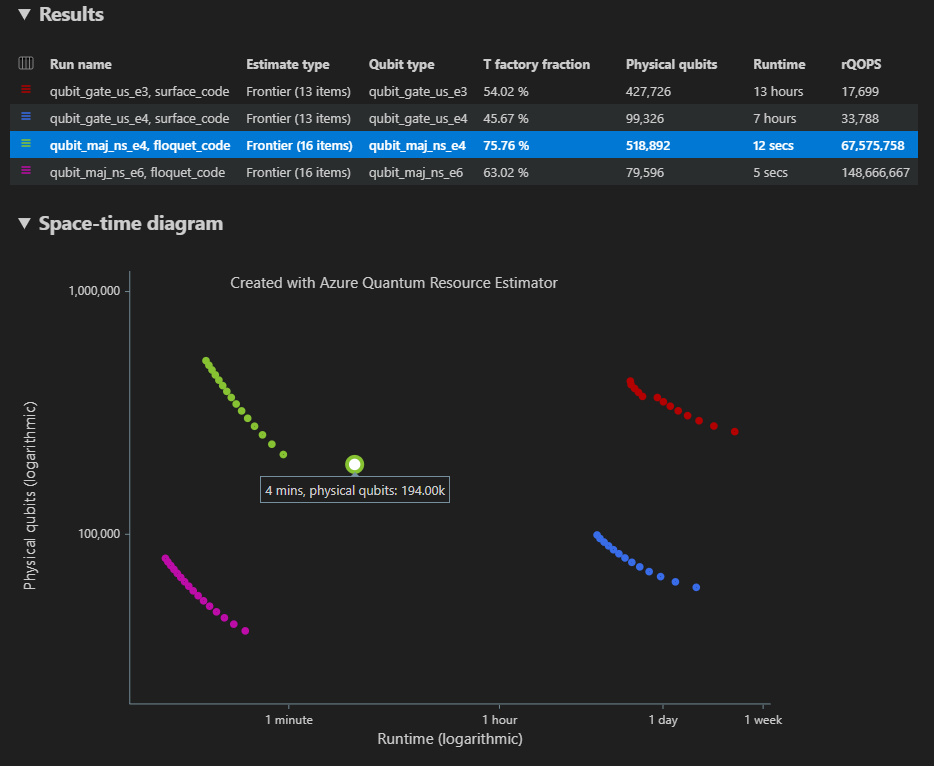
Щелкните {количество кубитов, среда выполнения} точки схемы пространства, чтобы открыть соответствующую схему пространства и данные отчета.
Предварительные требования для Jupyter Notebook в VS Code
Среда Python с установленным Python и Pip .
Последняя версия Visual Studio Code или откройте VS Code в Интернете.
VS Code с установленными расширениями Jupyter для Azure Quantum Development Kit, Python и Jupyter .
Последние версии Azure Quantum
qsharpиqsharp-widgetsпакетов.python -m pip install --upgrade qsharp qsharp-widgets
Совет
Для запуска локального оценщика ресурсов не требуется учетная запись Azure.
Создание квантового алгоритма
В VS Code выберите палитру команд view > и нажмите кнопку Create: New Jupyter Notebook.
В правом верхнем углу VS Code обнаружит и отобразит версию Python и виртуальную среду Python, выбранную для записной книжки. Если у вас несколько сред Python, может потребоваться выбрать ядро с помощью средства выбора ядра в правом верхнем углу. Если среда не обнаружена, сведения о настройке см . в записных книжках Jupyter Notebook в VS Code .
В первой ячейке записной книжки импортируйте
qsharpпакет.import qsharpДобавьте новую ячейку и скопируйте следующий код.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Оценка квантового алгоритма
Теперь вы оцениваете физические ресурсы для RunProgram операции с помощью допущений по умолчанию. Добавьте новую ячейку и скопируйте следующий код.
result = qsharp.estimate("RunProgram()")
result
Функция qsharp.estimate создает объект результата, который можно использовать для отображения таблицы с общим количеством физических ресурсов. Вы можете проверить сведения о затратах, совершите группы, которые содержат дополнительные сведения. Дополнительные сведения см . в полных отчетах о оценке ресурсов.
Например, свернуть группу параметров логического кубита, чтобы увидеть, что расстояние кода равно 21, а количество физических кубитов равно 882.
| Логический параметр кубита | Значение |
|---|---|
| Схема QEC | surface_code |
| Расстояние от кода | 21 |
| Физические кубиты | 882 |
| Время логического цикла | 8 миллисек |
| Частота ошибок логического кубита | 3.00E-13 |
| Пересечение префактотора | 0,03 |
| Порог исправления ошибок | 0,01 |
| Формула логического цикла | (4 * + twoQubitGateTime 2 * ) * oneQubitMeasurementTimecodeDistance |
| Формула физических кубитов | 2 * codeDistance * codeDistance |
Совет
Для более компактной версии выходной таблицы можно использовать result.summary.
Схема пространства
Распределение физических кубитов, используемых для алгоритма и фабрик T, является фактором, который может повлиять на структуру алгоритма. Пакет можно использовать qsharp-widgets для визуализации этого распределения, чтобы лучше понять предполагаемые требования к пространству для алгоритма.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
В этом примере количество физических кубитов, необходимых для выполнения алгоритма, 829766, 196686 которых являются кубитами алгоритмов и 633080 из которых являются кубитами фабрики T.

Изменение значений по умолчанию и оценка алгоритма
При отправке запроса оценки ресурсов для программы можно указать некоторые необязательные параметры. jobParams Используйте поле для доступа ко всем target параметрам, которые можно передать в выполнение задания, и просмотрите, какие значения по умолчанию были приняты:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Вы можете увидеть, что средство оценки ресурсов принимает qubit_gate_ns_e3 модель кубита, surface_code код исправления ошибок и бюджет ошибки 0.001 в качестве значений по умолчанию для оценки.
target Это параметры, которые можно настроить:
errorBudget— общий бюджет разрешенных ошибок для алгоритмаqecScheme— схема исправления квантовых ошибок (QEC)qubitParams— параметры физического кубитаconstraints— ограничения на уровне компонентаdistillationUnitSpecifications— спецификации для алгоритмов дистилляции фабрик TestimateType- один или граница
Дополнительные сведения см Target . в параметрах оценки ресурсов.
Изменение модели кубита
Вы можете оценить затраты для того же алгоритма с помощью параметра кубита на основе Майораны , qubitParams"qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Изменение схемы исправления квантовых ошибок
Вы можете повторно запустить задание оценки ресурсов для того же примера на параметрах кубита на основе Майораны с помощью флокеной схемы QEC. qecScheme
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Изменение бюджета ошибок
Затем повторно запустите тот же квантовый канал с errorBudget 10 %.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Пакетная обработка с помощью средства оценки ресурсов
Средство оценки квантовых ресурсов Azure позволяет выполнять несколько конфигураций target параметров и сравнивать результаты. Это полезно, если вы хотите сравнить стоимость различных моделей кубитов, схем QEC или бюджетов ошибок.
Вы можете выполнить пакетную оценку, передав список target параметров
paramsв параметрqsharp.estimateфункции. Например, выполните тот же алгоритм с параметрами по умолчанию и параметрами кубита на основе Majorana с помощью схемы QEC флокета.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Модель Логические кубиты Логическая глубина Состояния T Расстояние от кода Фабрики T Доля фабрики T Физические кубиты rQOPS Физическая среда выполнения Шлюз на основе ns, 10⁻️ 223 3.64M 4.70M 21 19 76.30 % 829.77k 26,55 млн 31 с Майорана ns, 10⁻⁶ 223 3.64M 4.70M 5 19 63.02 % 79.60k 148.67M 5 с Вы также можете создать список параметров оценки с помощью
EstimatorParamsкласса.from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Модель Логические кубиты Логическая глубина Состояния T Расстояние от кода Фабрики T Доля фабрики T Физические кубиты rQOPS Физическая среда выполнения Шлюз на основе μs, 10⁻️ 223 3.64M 4.70M 17 13 40.54 % 216.77k 21.86k 10 часов Шлюз на основе μs, 10⁻⁴ 223 3.64M 4.70M 9 14 43.17 % 63.57k 41.30k 5 часов Шлюз на основе ns, 10⁻️ 223 3.64M 4.70M 17 16 69.08 % 416.89k 32.79M 25 с Шлюз на основе ns, 10⁻⁴ 223 3.64M 4.70M 9 14 43.17 % 63.57k 61.94M 13 с Майорана ns, 10⁻⁴ 223 3.64M 4.70M 9 19 82.75 % 501.48k 82.59M 10 с Майорана ns, 10⁻⁶ 223 3.64M 4.70M 5 13 31.47 % 42.96k 148.67M 5 с
Выполнение оценки границ Парето
При оценке ресурсов алгоритма важно учитывать компромисс между количеством физических кубитов и средой выполнения алгоритма. Можно рассмотреть возможность выделения как можно больше физических кубитов, чтобы уменьшить среду выполнения алгоритма. Однако количество физических кубитов ограничено количеством физических кубитов, доступных в квантовом оборудовании.
Оценка границ Pareto предоставляет несколько оценок для одного и того же алгоритма, каждый из которых имеет компромисс между числом кубитов и средой выполнения.
Чтобы запустить оценку ресурсов с помощью оценки границ Pareto, необходимо указать
"estimateType"target параметр как"frontier". Например, выполните тот же алгоритм с параметрами кубита на основе Majorana с кодом поверхности с помощью оценки границ Pareto.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Функцию
EstimatesOverviewможно использовать для отображения таблицы с общим количеством физических ресурсов. Щелкните значок рядом с первой строкой, чтобы выбрать столбцы, которые нужно отобразить. Вы можете выбрать имя запуска, оценить тип, тип кубита, схему qec, бюджет ошибок, логические кубиты, логическую глубину, расстояние кода, T состояния, фабрики T, дробь фабрики T, среду выполнения, rQOPS и физические кубиты.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
В столбце "Оценка типа" таблицы результатов можно увидеть количество различных сочетаний {число кубитов, среда выполнения} для алгоритма. В этом случае оценка ресурсов находит 22 различных оптимальных сочетаний из многих тысяч возможных.
Схема времени
Эта EstimatesOverview функция также отображает схему времени оценки ресурсов.
На схеме пространства отображается количество физических кубитов и среда выполнения алгоритма для каждой пары {число кубитов, среда выполнения}. Вы можете навести указатель мыши на каждую точку, чтобы просмотреть сведения о оценке ресурсов на этом этапе.

Пакетная обработка с оценкой границы Pareto
Чтобы оценить и сравнить несколько конфигураций target параметров с оценкой границ, добавьте
"estimateType": "frontier",в параметры.result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])
Примечание.
С помощью
EstimatesOverviewфункции можно определить цвета и имена выполнения для схемы кубита времени.При выполнении нескольких конфигураций target параметров с помощью оценки границ Pareto можно просмотреть оценки ресурсов для определенной точки схемы времени, то есть для каждой пары {число кубитов, среда выполнения}. Например, в следующем коде показана оценка использования сведений для второго выполнения (оценка индекса=0) и кратчайшего времени выполнения (point index=3).
EstimateDetails(result[1], 4)Вы также можете увидеть схему пространства для определенной точки схемы пространства. Например, в следующем коде показана схема пространства для первого запуска сочетаний (оценка индекса=0) и третьего кратчайшего времени выполнения (индекс точки=2).
SpaceChart(result[0], 2)
Предварительные требования для Qiskit
- Учетная запись Azure с активной подпиской. Если у вас нет учетной записи Azure, зарегистрируйтесь бесплатно и зарегистрируйтесь для подписки с оплатой по мере использования.
- Рабочая область Azure Quantum. Дополнительные сведения см. в статье Создание рабочей области Azure Quantum.
Включение оценки target ресурсов Azure Quantum в рабочей области
Оценка ресурсов является поставщиком target Microsoft Quantum Computing. Если вы создали рабочую область с момента выпуска оценщика ресурсов, поставщик Microsoft Quantum Computing был добавлен в рабочую область автоматически.
Если вы используете существующую рабочую область Azure Quantum:
- Откройте рабочую область на портале Azure.
- На левой панели в разделе "Операции" выберите "Поставщики".
- Нажмите кнопку +Добавить поставщика.
- Выберите + Добавить для Microsoft Quantum Computing.
- Выберите "Узнать" и " Разработка " и нажмите кнопку "Добавить".
Создание записной книжки в рабочей области
- Войдите на портал Azure и выберите рабочую область Azure Quantum.
- В разделе "Операции" выберите "Записные книжки"
- Щелкните "Мои записные книжки" и нажмите кнопку "Добавить новую"
- В разделе Тип ядра выберите IPython.
- Введите имя файла и нажмите кнопку "Создать файл".
При открытии новой записной книжки он автоматически создает код для первой ячейки на основе сведений о подписке и рабочей области.
from azure.quantum import Workspace
workspace = Workspace (
resource_id = "", # Your resource_id
location = "" # Your workspace location (for example, "westus")
)
Примечание.
Если не указано иное, следует выполнять ячейки в порядке их создания, чтобы избежать проблем компиляции.
Щелкните треугольный значок воспроизведения слева от ячейки, чтобы выполнить размещенный в ней код.
Загрузка необходимых объектов импорта
Сначала необходимо импортировать дополнительные модули из azure-quantum и qiskit.
Щелкните + Код, чтобы добавить новую ячейку, а затем добавьте и выполните следующий код:
from azure.quantum.qiskit import AzureQuantumProvider
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import RGQFTMultiplier
Подключение к службе Azure Quantum
Затем создайте объект AzureQuantumProvider с помощью workspace объекта из предыдущей ячейки для подключения к рабочей области Azure Quantum. Вы создаете внутренний экземпляр и задаете в качестве targetоценщика ресурсов.
provider = AzureQuantumProvider(workspace)
backend = provider.get_backend('microsoft.estimator')
Создание квантового алгоритма
В этом примере вы создадите квантовый канал для умножения на основе конструкции, представленной в Ruiz-Perez и Garcia-Escartin (arXiv:1411.5949), которая использует преобразование Quantum Fourier для реализации арифметики.
Можно изменить размер умножения, изменив bitwidth переменную. Создание канала упаковывается в функцию, которую можно вызвать со bitwidth значением умножения. Операция будет иметь два входных регистра, каждый размер указанного bitwidthи один выходной регистр, который в два раза превышает указанный bitwidth. Функция также выводит некоторые логические счетчики ресурсов для умножения, извлеченного непосредственно из квантового канала.
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
# Print a warning for large bitwidths that will require some time to generate and
# transpile the circuit.
if bitwidth > 18:
print(f"[WARN] It will take more than one minute generate a quantum circuit with a bitwidth larger than 18")
circ = RGQFTMultiplier(num_state_qubits=bitwidth, num_result_qubits=2 * bitwidth)
# One could further reduce the resource estimates by increasing the optimization_level,
# however, this will also increase the runtime to construct the algorithm. Note, that
# it does not affect the runtime for resource estimation.
print(f"[INFO] Decompose circuit into intrinsic quantum operations")
circ = transpile(circ, basis_gates=SUPPORTED_INSTRUCTIONS, optimization_level=0)
# print some statistics
print(f"[INFO] qubit count: {circ.num_qubits}")
print("[INFO] gate counts")
for gate, count in circ.count_ops().items():
print(f"[INFO] - {gate}: {count}")
return circ
Примечание.
Вы можете отправлять задания оценки физических ресурсов для алгоритмов, которые не имеют состояний T, но имеют по крайней мере одно измерение.
Оценка квантового алгоритма
Создайте экземпляр алгоритма с помощью create_algorithm функции. Можно изменить размер умножения, изменив bitwidth переменную.
bitwidth = 4
circ = create_algorithm(bitwidth)
Оцените физические ресурсы для этой операции с помощью допущений по умолчанию. Канал можно отправить в серверную часть resource Estimator с помощью run метода, а затем запустить job.result() , чтобы дождаться завершения задания и возврата результатов.
job = backend.run(circ)
result = job.result()
result
При этом создается таблица, показывающая общее количество физических ресурсов. Вы можете проверить сведения о затратах, совершите группы, которые содержат дополнительные сведения.
Совет
Для более компактной версии выходной таблицы можно использовать result.summary.
Например, если свернуть группу параметров логического кубита, проще увидеть, что расстояние кода исправления ошибок равно 15.
| Логический параметр кубита | Значение |
|---|---|
| Схема QEC | surface_code |
| Расстояние от кода | 15 |
| Физические кубиты | 450 |
| Время логического цикла | 6us |
| Частота ошибок логического кубита | 3.00E-10 |
| Пересечение префактотора | 0,03 |
| Порог исправления ошибок | 0,01 |
| Формула логического цикла | (4 * + twoQubitGateTime 2 * ) * oneQubitMeasurementTimecodeDistance |
| Формула физических кубитов | 2 * codeDistance * codeDistance |
В группе параметров физического кубита вы увидите свойства физического кубита, которые были предполагались для этой оценки. Например, время выполнения измерения с одним кубитом и однокубитных шлюзов предполагается, что 100 ns и 50 ns соответственно.
Совет
Вы также можете получить доступ к выходным данным средства оценки ресурсов в качестве словаря Python с помощью метода result.data().
Дополнительные сведения см . в полном списке выходных данных для средства оценки ресурсов.
Схемы пространства
Распределение физических кубитов, используемых для алгоритма и фабрик T, является фактором, который может повлиять на структуру алгоритма. Вы можете визуализировать это распределение, чтобы лучше понять предполагаемые требования к пространству для алгоритма.
result.diagram.space
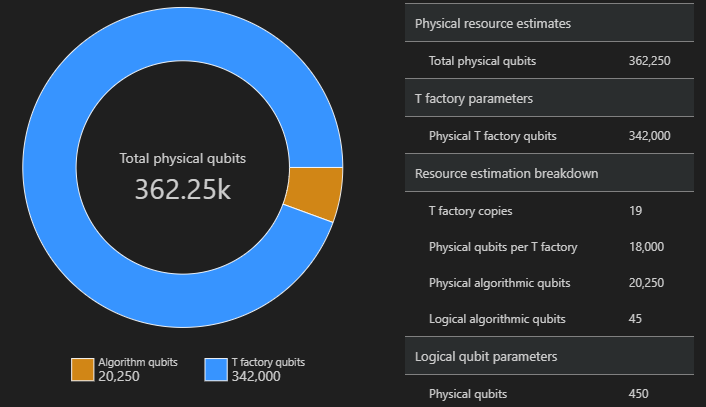
На схеме пространства показана доля кубитов алгоритмов и кубитов фабрики T. Обратите внимание, что количество копий фабрики T, 28, способствует количеству физических кубитов для фабрик T как $\text{T фабрик} \cdot \text{физический кубит на фабрику T}= 28 \cdot 18 000 = 504 000$.
Дополнительные сведения см. в разделе "Физическая оценка фабрики T".
Изменение значений по умолчанию и оценка алгоритма
При отправке запроса оценки ресурсов для программы можно указать некоторые необязательные параметры. jobParams Используйте поле для доступа ко всем значениям, которые можно передать в выполнение задания, и просмотрите, какие значения по умолчанию были приняты:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
target Это параметры, которые можно настроить:
errorBudget— общий бюджет разрешенных ошибокqecScheme— схема исправления квантовых ошибок (QEC)qubitParams— параметры физического кубитаconstraints— ограничения на уровне компонентаdistillationUnitSpecifications— спецификации для алгоритмов дистилляции фабрик T
Дополнительные сведения см Target . в параметрах оценки ресурсов.
Изменение модели кубита
Затем оцените затраты на тот же алгоритм с помощью параметра кубита на основе Майораны qubit_maj_ns_e6
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
})
result = job.result()
result
Вы можете программным образом проверить физические счетчики. Например, можно изучить сведения о фабрике T, созданной для выполнения алгоритма.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Примечание.
По умолчанию среда выполнения отображается в наносекундах.
Эти данные можно использовать для создания некоторых объяснений того, как фабрики T производят необходимые состояния T.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numModulesPerRound"][round]} {tfactory["moduleNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Изменение схемы исправления квантовых ошибок
Теперь повторно запустите задание оценки ресурсов для того же примера на параметрах кубита на основе Майораны с помощью флокой схемы QEC. qecScheme
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
},
qecScheme={
"name": "floquet_code"
})
result_maj_floquet = job.result()
result_maj_floquet
Изменение бюджета ошибок
Давайте повторно запустите тот же квантовый канал с errorBudget 10 %.
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
},
qecScheme={
"name": "floquet_code"
},
errorBudget=0.1)
result_maj_floquet_e1 = job.result()
result_maj_floquet_e1
Примечание.
Если при работе с оценщиком ресурсов возникла проблема, ознакомьтесь со страницей "Устранение неполадок" или обратитесь к ней.AzureQuantumInfo@microsoft.com