Självstudie: Implementera en kvantgenerator för slumptal i Q#

Artikel
07/03/2024

I den här självstudien lär du dig att skriva ett grundläggande kvantprogram som Q# utnyttjar kvantmekanikens natur för att skapa ett slumpmässigt tal.

I den här självstudien kommer vi att:

Skapa ett Q# program.
Granska huvudkomponenterna i ett Q# program.
Definiera logiken för ett problem.
Kombinera klassiska åtgärder och kvantåtgärder för att lösa ett problem.
Arbeta med qubitar och superposition för att skapa en slumpgenerator för kvanttal.

Dricks

Om du vill påskynda din kvantberäkningsresa kan du kolla in Kod med Azure Quantum, en unik funktion på Azure Quantum-webbplatsen. Här kan du köra inbyggda Q# exempel eller egna Q# program, generera ny Q# kod från dina frågor, öppna och köra koden i VS Code för webben med ett klick och ställa frågor till Copilot om kvantberäkning.

Förutsättningar

Så här kör du kodexemplet i Copilot i Azure Quantum:
- Ett Microsoft-e-postkonto (MSA).
Så här utvecklar och kör du kodexemplet i Visual Studio Code:
- Den senaste versionen av Visual Studio Code eller öppna VS Code på webben.
- Den senaste versionen av Azure-tilläggetQuantum Development Kit. Installationsinformation finns i Installera QDK på VS Code.
- Om du vill använda Jupyter Notebooks måste du också installera Python- och Jupyter-tillägg och det senaste Python-paketetqsharp. Det gör du genom att öppna en terminal och köra följande kommando:
```
$ pip install --upgrade  qsharp
```

Definiera problemet

Klassiska datorer producerar inte slumpmässiga tal, utan snarare pseudorandomnummer . En pseudorandomtalgenerator genererar en deterministisk sekvens med tal baserat på ett initialt värde, kallat seed. För att ge tal som är mer slumpmässiga utgörs seed oftast av den aktuella tiden från CPU-klockan.

Kvantdatorer kan å andra sidan generera verkligt slumpmässiga tal. Det beror på att mätningen av en kvantbit i superposition är en probabilistisk process. Resultatet av mätningen är slumpmässigt och det finns inget sätt att förutsäga resultatet. Detta är den grundläggande principen för kvant slumptalsgeneratorer.

En kvantbit är en enhet med kvantinformation som kan finnas i superposition. När den mäts kan en kvantbit bara vara i tillståndet 0 eller 1 . Före mätningen representerar kvantbitens tillstånd dock sannolikheten att läsa antingen 0 eller 1 med en mätning.

Du börjar med att ta en kvantbit i ett bastillstånd, till exempel noll. Det första steget i slumptalsgeneratorn är att använda en Hadamard-åtgärd för att placera kvantbiten i en lika stor superposition. Mätningen av det här tillståndet resulterar i en nolla eller en med 50 % sannolikhet för varje utfall, en verkligt slumpmässig bit.

Det finns inget sätt att veta vad du får efter mätningen av kvantbiten i superposition, och resultatet är ett annat värde varje gång koden anropas. Men hur kan du använda det här beteendet för att generera större slumpmässiga tal?

Anta att du upprepar processen fyra gånger och genererar den här sekvensen med binära siffror:

$${0, 1, 1, 0}$$

Om du sammanfogar, eller kombinerar, dessa bitar till en bitsträng kan du skapa ett större tal. I det här exemplet motsvarar bitsekvensen ${0110}$ talet sex i decimalsystemet.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

Om du upprepar den här processen många gånger kan du kombinera flera bitar för att bilda ett stort tal. Nu kan du ange ditt överordnade med det numret som ett säkert lösenord, eftersom du kan vara säker på att ingen space hacker kan fastställa resultatet av sekvensen av mätningar.

Definiera logiken för slumptalsgeneratorn

Nu ska vi beskriva logiken för en slumptalsgenerator, förutsatt att vi har en slumpmässig bitgenerator:

Definiera max som det högsta antal som du vill generera.
Definiera antalet slumpmässiga bitar som du behöver generera. Detta görs genom beräkning av hur många bitar, nBits, vi måste uttrycka heltal för upp till max.
Generera en slumpmässig bitsträng som har längden nBits.
Om bitsträngen representerar ett tal som är större än max går du tillbaka till steg tre.
I annat fall är processen slutförd. Returnera det genererade talet som ett heltal.

Som exempel anger vi max till 12. Det vill: 12 är det största talet som du vill använda som ett säkert lösenord.

Du behöver ${\lfloor ln(12) / ln(2) + 1 \rfloor}$, eller 4 bitar för att representera ett tal mellan 0 och 12. (För att hålla det här kortfattat hoppar vi över hur man deriverar den här ekvationen.)

Anta att du genererar bitsträngen ${1101_{\ binary}}$, som motsvarar ${13_{\ decimal}}$. Eftersom 13 är större än 12 upprepar du processen.

Sedan generar du bitsträngen ${0110_{\ binary}}$, som motsvarar ${6_{\ decimal}}$. Eftersom 6 är mindre än 12 är processen slutförd.

Kvantgeneratorn för slumptal returnerar nummer 6 som lösenord. I praktiken anger du ett större tal som högsta eftersom lägre tal är lätta att knäcka genom att bara prova alla möjliga lösenord. För att öka svårigheten att gissa eller knäcka lösenordet kan du använda ASCII-kod för att konvertera binär till text och generera ett lösenord med hjälp av siffror, symboler och gemener.

Skriva en slumpmässig bitgenerator

Det första steget är att skriva en Q# åtgärd som genererar en slumpmässig bit. Den här åtgärden är en av byggstenarna i slumptalsgeneratorn.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Ta nu en titt på ny kod.

Du definierar åtgärden GenerateRandomBit , som inte tar några indata och genererar ett värde av typen Result. Typen Result representerar resultatet av en mätning och kan ha två möjliga värden: Zero eller One.
Du allokerar en enda qubit med nyckelordet use . När den allokeras är en qubit alltid i tillståndet Zero .
Du använder åtgärden H för att placera kvantbiten i en lika stor superposition.
Du använder åtgärden M för att mäta kvantbiten, returnera det uppmätta värdet (Zero eller One).
Du använder åtgärden Reset för att återställa kvantbiten till tillståndet |0〉.

Genom att placera kvantbiten i superposition med H åtgärden och mäta den med M åtgärden blir resultatet ett annat värde varje gång koden anropas.

Visualisera Q# koden med Bloch-sfären

I Bloch-sfären representerar nordpolen det klassiska värdet 0 och sydpolen det klassiska värdet 1. Alla superpositioner kan representeras av en punkt på sfären (visas med en pil). Ju närmare pilen är en pol, desto högre är sannolikheten att kvantbiten minimeras till det klassiska värde som tilldelades till polen när den mättes. Till exempel har kvantbitstillståndet som representeras av pilen i följande bild en högre sannolikhet att ge värdet 0 om du mäter det.

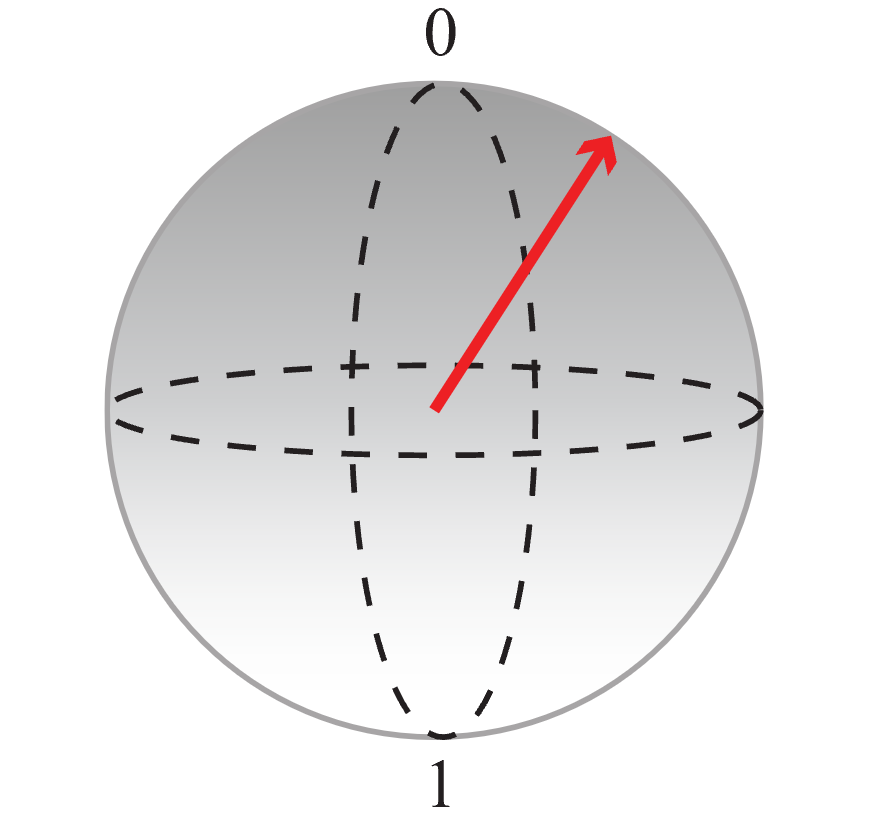
Ett diagram som visar ett qubittillstånd med hög sannolikhet att mäta noll.

Du kan använda den här representationen för att visualisera vad koden gör:

Börja först med en qubit som initierats i tillståndet 0 och tillämpa en H åtgärd för att skapa en lika stor superposition där sannolikheterna för 0 och 1 är desamma.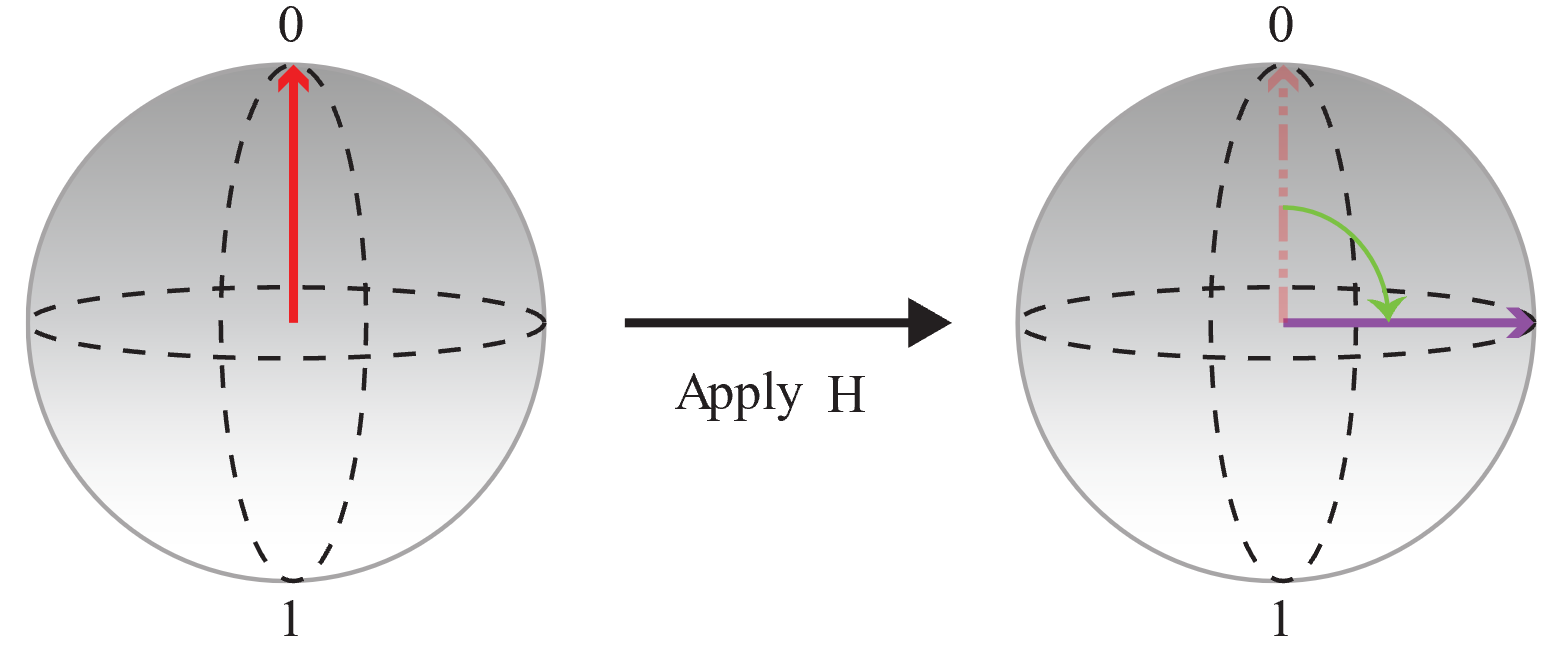
Mät sedan kvantbiten och spara utdata:

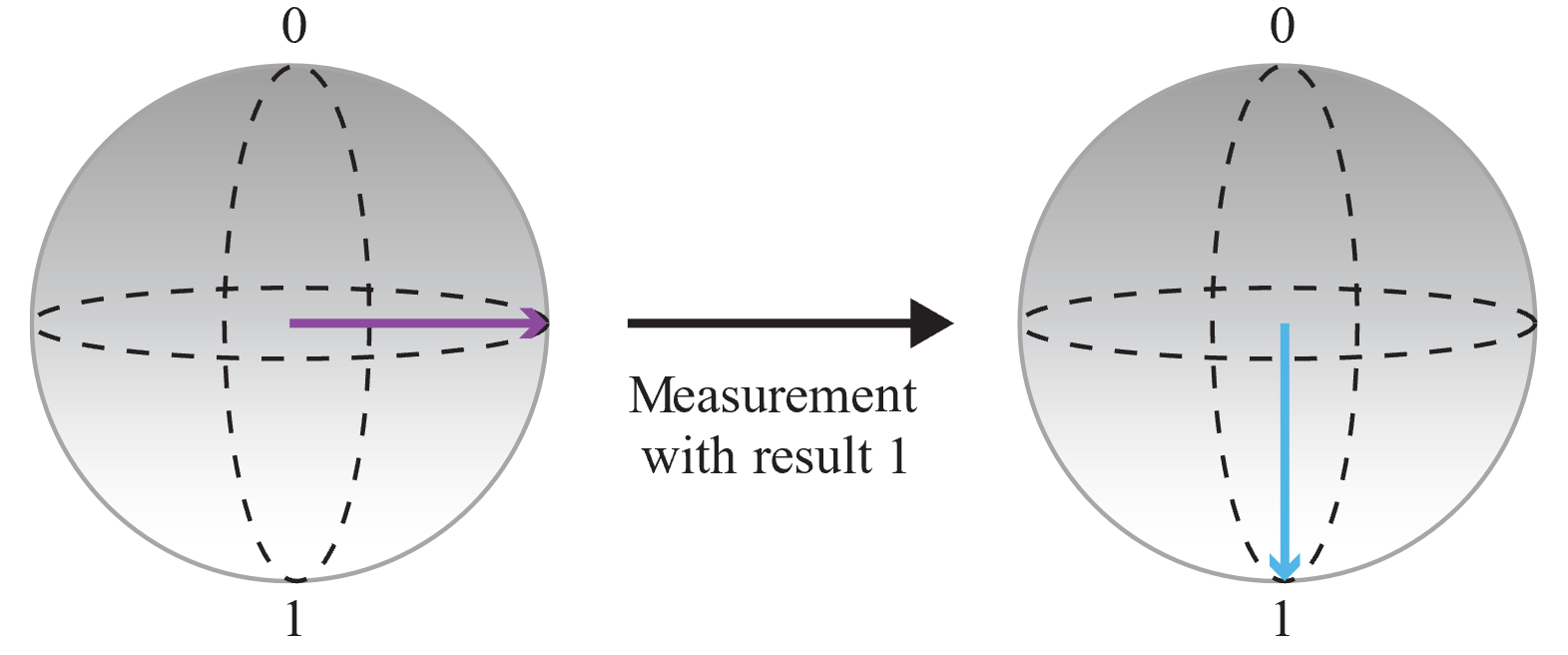
Eftersom resultatet av mätningen är slumpmässigt och sannolikheten för att mäta 0 och 1 är densamma har du fått en helt slumpmässig bit. Du kan anropa den här åtgärden flera gånger för att skapa heltal. Om du till exempel anropar åtgärden tre gånger för att hämta tre slumpmässiga bitar kan du skapa slumpmässiga 3-bitars tal (det vill säga ett slumpmässigt tal mellan 0 och 7).

Skriva en fullständig slumptalsgenerator

Först måste du lägga till de nödvändiga Q# namnrymderna i programmet. För den fullständiga slumptalsgeneratorn måste du inkludera tre Q# namnområden: Microsoft.Quantum.Math, Microsoft.Quantum.Intrinsicoch Microsoft.Quantum.Convert.
```
open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Math;
```
Därefter definierar du åtgärden GenerateRandomNumberInRange . Den här åtgärden anropar åtgärden GenerateRandomBit upprepade gånger för att bygga en sträng med bitar.
```
    /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }
```
Vi tar och går igenom den nya koden.
- Du måste beräkna antalet bitar som behövs för att uttrycka heltal upp till max. Funktionen BitSizeI från Microsoft.Quantum.Math namnområdet konverterar ett heltal till det antal bitar som behövs för att representera det.
- Åtgärden SampleRandomNumberInRange använder en for-loop för att generera slumpmässiga tal tills den genererar ett som är lika med eller mindre än max. Loopen for fungerar exakt på samma sätt som en for loop i andra programmeringsspråk.
- Variabeln bits är en föränderlig variabel. Föränderliga variabler kan ändras under beräkningen. Du kan använda direktivet set för att ändra värdet för en föränderlig variabel.
- Funktionen ResultArrayAsInt kommer från Microsoft.Quantum.Convert namnområdet. Den här funktionen konverterar bitsträngen till ett positivt heltal.
Slutligen lägger du till en startpunkt. I det här exemplet är åtgärden Main startpunkten för programmet. Den anropar GenerateRandomNumberInRange åtgärden för att generera ett slumpmässigt tal mellan 0 och 100.
```
    @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }
```
Direktivet let deklarerar variabler som inte ändras under beräkningen. Här definierar vi det maximala värdet som 100.
Den fullständiga koden för slumptalsgeneratorn är följande:

namespace QuantumRandomNumberGenerator {
    open Microsoft.Quantum.Convert;
    open Microsoft.Quantum.Intrinsic;
    open Microsoft.Quantum.Math;

    @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }

    /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }

    operation GenerateRandomBit() : Result {
        // Allocate a qubit.
        use q = Qubit();

        // Set the qubit into superposition of 0 and 1 using the Hadamard 
        H(q);

        // At this point the qubit `q` has 50% chance of being measured in the
        // |0〉 state and 50% chance of being measured in the |1〉 state.
        // Measure the qubit value using the `M` operation, and store the
        // measurement value in the `result` variable.
        let result = M(q);

        // Reset qubit to the |0〉 state.
        // Qubits must be in the |0〉 state by the time they are released.
        Reset(q);

        // Return the result of the measurement.
        return result;
    }
}

Kör slumptalsgeneratorprogrammet

Du kan köra programmet i Copilot i Azure Quantum och i Visual Studio Code som ett fristående Q# program eller med hjälp av ett Python-värdprogram.

Du kan testa din Q# kod med Copilot i Azure Quantum kostnadsfritt – allt du behöver är ett Microsoft-e-postkonto (MSA). Mer information om Copilot i Azure Quantum finns i Utforska Azure Quantum.

Öppna Copilot i Azure Quantum i webbläsaren.

Kopiera och klistra in följande kod i kodredigeraren.

namespace Tutorial {
    open Microsoft.Quantum.Convert;
    open Microsoft.Quantum.Intrinsic;
    open Microsoft.Quantum.Math;

    @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }

    /// # Summary
    /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }

    /// # Summary
    /// Generates a random bit.
    operation GenerateRandomBit() : Result {
        // Allocate a qubit.
        use q = Qubit();

        // Set the qubit into superposition of 0 and 1 using the Hadamard 
        // operation `H`.
        H(q);

        // At this point the qubit `q` has 50% chance of being measured in the
        // |0〉 state and 50% chance of being measured in the |1〉 state.
        // Measure the qubit value using the `M` operation, and store the
        // measurement value in the `result` variable.
        let result = M(q);

        // Reset qubit to the |0〉 state.
        // Qubits must be in the |0〉 state by the time they are released.
        Reset(q);

        // Return the result of the measurement.
        return result;

        // Note that Qubit `q` is automatically released at the end of the block.
    }
}

Välj antalet bilder som ska köras och klicka på Kör.
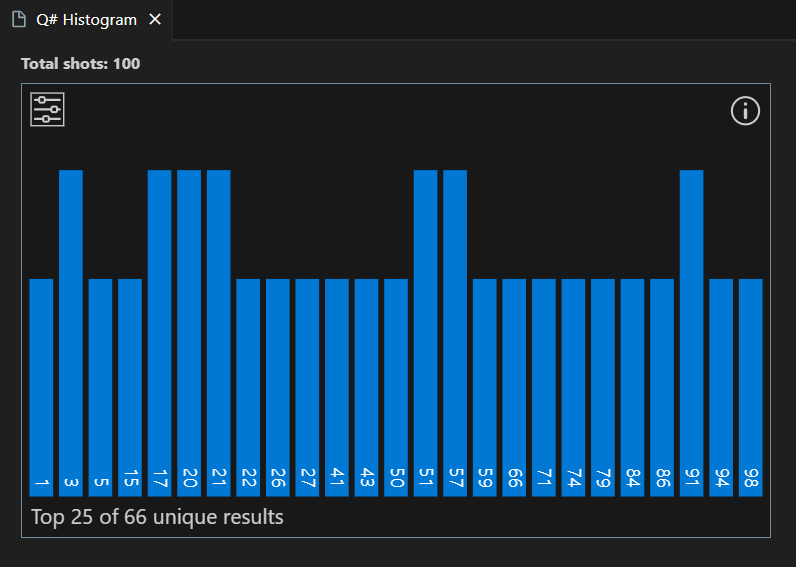
Resultaten visas i histogrammet och i fälten Resultat .
Klicka på Förklara kod för att uppmana Copilot att förklara koden för dig.

Dricks

Från Copilot i Azure Quantum kan du öppna programmet i VS Code för webben genom att klicka på VS Code-logotypknappen i det högra hörnet i kodredigeraren.

Öppna Visual Studio Code och välj Fil > Ny textfil för att skapa en ny fil.
Spara filen som RandomNumberGenerator.qs. Den här filen innehåller Q# koden för ditt program.

Kopiera följande kod i RandomNumberGenerator.qs filen.

namespace Tutorial {
    open Microsoft.Quantum.Convert;
    open Microsoft.Quantum.Intrinsic;
    open Microsoft.Quantum.Math;

    @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }

    /// # Summary
    /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }

    /// # Summary
    /// Generates a random bit.
    operation GenerateRandomBit() : Result {
        // Allocate a qubit.
        use q = Qubit();

        // Set the qubit into superposition of 0 and 1 using the Hadamard 
        // operation `H`.
        H(q);

        // At this point the qubit `q` has 50% chance of being measured in the
        // |0〉 state and 50% chance of being measured in the |1〉 state.
        // Measure the qubit value using the `M` operation, and store the
        // measurement value in the `result` variable.
        let result = M(q);

        // Reset qubit to the |0〉 state.
        // Qubits must be in the |0〉 state by the time they are released.
        Reset(q);

        // Return the result of the measurement.
        return result;

        // Note that Qubit `q` is automatically released at the end of the block.
    }
}

Innan du kör programmet måste du ange profilen target till Obegränsad. Välj Visa –> Kommandopalett, sök efter QIR, välj Q#: Ange Azure Quantum QIR-profilentarget och välj Q#sedan : obegränsad.
Om du vill köra programmet väljer du Kör fil i listrutan uppspelningsikonen längst upp till höger, klickar på Kör i listan med kommandon nedan @EntryPoint()eller trycker på Ctrl+F5.Q# Programmet kör åtgärden eller funktionen som markerats med @EntryPoint() attributet i standardsimulatorn.
Dina utdata visas i felsökningskonsolen.
Kör programmet igen för att se ett annat resultat.

Kommentar

Om profilen target inte är inställd på Obegränsad får du ett fel när du kör programmet.

Rita frekvens histogram

Nu ska vi visualisera fördelningen av resultat som hämtats från att köra kvantprogrammet flera gånger. Frekvens histogrammet hjälper till att visualisera sannolikhetsfördelningen för dessa resultat.

Välj Visa –> Kommandopalett och skriv "histogram" som ska ta upp Q#: Kör-filen och visa histogramalternativet . Du kan också klicka på Histogram från listan med kommandon nedan @EntryPoint(). Välj det här alternativet för att öppna Q# histogramfönstret.
Ange ett antal bilder för att köra programmet, till exempel 100 bilder, och tryck på Retur. Histogrammet visas i Q# histogramfönstret.
Varje stapel i histogrammet motsvarar ett möjligt utfall och dess höjd representerar antalet gånger som resultatet observeras. Antalet olika resultat kan variera varje gång du kör histogrammet.

Dricks

Du kan zooma histogrammet med hjälp av musrullningshjulet eller en styrplatta. När du är inzoomad kan du panorera diagrammet genom att trycka på Alt medan du rullar.
Klicka på ett fält för att visa procentandelen av resultatet.
Klicka på ikonen för inställningar längst upp till vänster för att visa alternativ. Du kan visa de 10 bästa resultaten, de 25 bästa resultaten eller alla resultat. Du kan också sortera resultaten från hög till låg eller låg till hög.

I VS Code väljer du Visa > kommandopalett och väljer Skapa: Ny Jupyter Notebook.
I den första cellen qsharp importerar du paketet i Python-koden:
```
import qsharp
```

Q# Lägg till koden för kvantgeneratorprogrammet för slumptal. För att göra det använder du det %%qhsarp magiska kommandot. Observera att %%qsharp kommandot ändrar notebook-cellen från typ Python till typ Q#. Kopiera den här koden till den andra cellen.

%%qsharp

open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Math;

@EntryPoint()
operation Main() : Int {
    let max = 100;

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Kör slutligen koden. Du kan köra samma simulering ett antal gånger, oberoende av varandra. Varje oberoende simulering kallas "shot". Vi kör till exempel simuleringen 100 gånger.
```
results = qsharp.run("Main()", shots=100)
print(results)
```

Kommentar

Det här kodfragmentet körs för närvarande inte på någon tillgänglig Azure Quantum-maskinvara targetseftersom anropsbar ResultArrayAsInt kräver en QPU med fullständig beräkningsprofil.

Utforska andra Q# självstudier:

Kvantsammanflätning visar hur du skriver ett Q# program som manipulerar och mäter kvantbitar och visar effekterna av superposition och sammanflätning.
Grover sökalgoritm visar hur du skriver ett Q# program som använder Grover sökalgoritm.
Quantum Fourier Transforms utforskar hur du skriver ett Q# program som direkt adresserar specifika kvantbitar.
Quantum Katas är självstudier och programmeringsövningar som syftar till att lära ut elementen i kvantberäkning och Q# programmering på samma gång.

Dela via

Självstudie: Implementera en kvantgenerator för slumptal i Q#

Förutsättningar

Definiera problemet

Definiera logiken för slumptalsgeneratorn

Skriva en slumpmässig bitgenerator

Visualisera Q# koden med Bloch-sfären

Skriva en fullständig slumptalsgenerator

Kör slumptalsgeneratorprogrammet

Rita frekvens histogram

Feedback

Feedback

Ytterligare resurser

Dela via

Självstudie: Implementera en kvantgenerator för slumptal i Q#

Förutsättningar

Definiera problemet

Definiera logiken för slumptalsgeneratorn

Skriva en slumpmässig bitgenerator

Visualisera Q# koden med Bloch-sfären

Skriva en fullständig slumptalsgenerator

Kör slumptalsgeneratorprogrammet

Relaterat innehåll

Feedback

Feedback

Ytterligare resurser