Fastställa den optimala kombinationen av överlappande rabatter

Fastställa den optimala kombinationen av överlappande rabatter i Microsoft Dynamics 365 Commerce.

När rabatterna överlappar måste du fastställ vilken kombination av överlappande rabatter som ger det lägsta transaktionssumman eller den högsta rabattsumman. När rabattbeloppet varierar beroende på priset på de produkter som köps, så som den vanliga butiksrabatten "Köp en, få en X procent rabatt" (BOGO), blir processen en fråga om kombinatorisk optimering.

Den här artikeln avser Microsoft Dynamics AX 2012 R3 KB 3105973 (utgiven 2 november 2015) eller senare och till Dynamics 365 Commerce. För att fastställa kombinationen av överlappande rabatter som ska tillämpas vid rätt tidpunkt har vi introducerat en metod för att använda överlappande rabatter. Den nya metoden kallas marginalvärderankning. I metoden marginalvärderankning beräknas ett värde för varje överlappande rabatt genom att använda rabattvärdet på de delade produkterna. Överlappande rabatter tillämpas sedan från det högsta relativa värdet till det lägsta relativa värdet. Mer information om den nya metoden finns i avsnittet marginalvärderankning nedan. Marginalvärderankning används inte när rabattbeloppen för en produkt inte påverkas av en annan produkt i transaktionen. Denna metod används exempelvis inte för två enkla rabatter, eller för en enkel rabatt och en enda produktkvantitetsrabatt.

Exempel på rabatter

Du kan skapa ett obegränsat antal rabatter för en gemensam uppsättning produkter. Men eftersom det inte finns någon gräns kan prestandaproblem uppstå när du försöker att beräkna rabatterna som ska användas för de olika produkterna. Följande exempel visar det här problemet i detalj. I exempel 1 börjar vi med två produkter och två överlappande rabatter. Sedan, i exempel 2, visar vi hur problemet utvecklas när fler produkter läggs till.

Exempel 1: Två produkter och två rabatter

I det här exemplet krävs två produkter för att kvalificera sig för varje rabatt och rabatterna kan inte kombineras. Rabatterna i det här exemplet är Bästa pris-rabatter. Båda produkterna uppfyller kraven för båda rabatterna. Här följer två rabatter.

För två valfria produkter vilar den bättre av dessa två rabatter på priserna för de två produkterna. När priset för båda produkterna är nästan lika eller lika, är rabatt 1 bättre. När priset på en produkt är betydligt mindre än priset på den andra produkten, är rabatt 2 bättre. Här följer den matematiska regeln för att bedöma dessa två rabatter mot varandra.

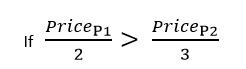
Notering

När priset för produkt 1 är lika med två tredjedelar av priset för produkt 2, väger de två rabatterna lika. I det här exemplet varierar rabattprocenten för rabatt 1 från några procent (när priserna för de två produkterna ligger långt från varandra) till högst 25 procent (när de två produkterna har samma pris). Den effektiv rabattprocenten för rabatt 2 är fast. Den är alltid 20 procent. Eftersom den effektiva rabattprocenten för rabatten 1 har ett intervall som kan vara mer än eller mindre än rabatt 2 är den bästa rabatten beroende av priserna för de två produkter som måste rabatteras. I det här exemplet slutfördes beräkningen snabbt, eftersom endast två rabatter tillämpas på endast två produkter. Det finns två möjliga kombinationer: ett användning av rabatt 1 eller en användning av rabatt 2. Det finns inga permutationer att beräkna. Värdet för varje rabatt beräknas med hjälp av båda produkterna och bästa rabatten används.

Exempel 2: Fyra produkter och två rabatter

Nu ska använda fyra produkter och samma två rabatter. Alla fyra produkterna uppfyller kraven för båda rabatterna. Det finns tolv möjliga kombinationer. I slutändan ska två rabatter användas på transaktionen i någon av tre kombinationer: två användningar av rabatt 1, två användningar av rabatt 2 eller en användning av rabatt 1 och en användning av rabatt 2. För att illustrera de möjliga kombinationerna ska vi titta på två olika uppsättningar med fyra produkter som har olika priser:

• Alla fyra produkterna har samma pris, $15,00. I det här fallet är den bästa kombinationen två användningar av rabatt 1. Två produkter får fullt pris och två får 50 procent rabatt. Den rabatterade summan för transaktionen är $45 (15 + 15 + 7,50 + 7,50), vilket är $15 (25 procent) av den orabatterade summan på $60. Rabatt 2 är bara $12 (20 procent).
• Två produkter kostar $20 var, en produkt koster $15 och en produkt kostar $5. I det här fallet är den bästa kombinationen en användning av rabatt 2 och en användning av rabatt 1. Följande tabeller visar rabatterna.

För att läsa tabellerna, använd en produkt från en rad och en produkt från en kolumn. Till exempel i tabellen för rabatt 1, när du kombinerar de två $20-produkterna, får du $10 rabatt. I tabellen för rabatt 2, när du kombinerar $15-produkten och $5-produkten, får du $4 rabatt.

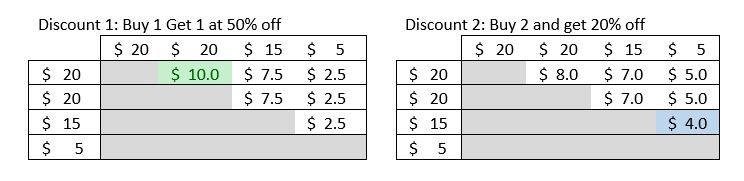
Först letar vi reda på den största möjliga rabatten för två produkter genom att använda någondera av rabatterna. De två tabellerna visar rabattbeloppet för alla kombinationer av de två produkterna. Den skuggade delen av tabellerna representerar antingen fall där en produkt är ihopparad med sig själv, vilket vi inte kan göra, eller en omvänd ihopparning av två produkter som ger samma rabattbelopp och kan ignoreras. Genom att titta i tabellerna ser du att rabatt 1 för de två $20-artiklarna är den största möjliga rabatten för någon rabatt på alla fyra produkterna. (Den här rabatten markeras med grönt i den första tabellen.) Kvar finns då $15-produkten och $5-produkten. Genom att titta på de två tabellerna igen ser du att rabatt 1 för dessa två produkter ger en rabatt på $2,50, medan rabatt 2 ger en rabatt på $4. Vi väljer därför rabatt 2. Totalrabatten är $14. För att göra den här diskussionen enklare att visualisera är här två ytterligare tabeller som visar den effektiva rabattprocenten för alla möjliga kombinationer av två produkter för både rabatt 1 och rabatt 2. Endast halva listan över kombinationer ingår, eftersom det för dessa två rabatter inte spelar någon roll i vilken ordning de två produkterna tas med i rabatten. Den högsta effektiva rabatten (25 procent)markeras med grönt och lägsta effektiva rabatten (10 procent) markeras i rött.

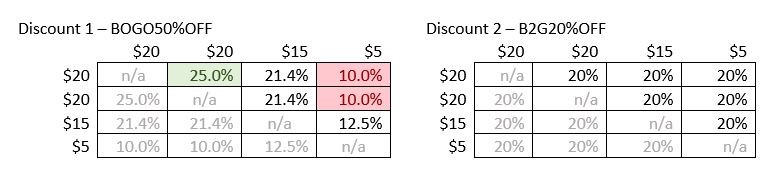
Notering

När priserna varierar, och två eller flera rabatter konkurrerar, är det enda sättet att garantera den bästa rabattkombinationen att utvärdera båda rabatter och jämföra dem.

Totalt antal möjliga kombinationer

Det här avsnittet fortsätter med exemplet i det föregående avsnittet. Vi ska lägga till fler produkter och ytterligare en rabatt och se hur många kombinationer som måste beräknas och jämförs. Tabellen nedan visar antalet möjliga rabattkombinationer allt eftersom produktkvantiteten ökar. I tabellen visas vad som händer, både när det finns två överlappande rabatter, som i föregående exempel, och när det finns tre överlappande rabatter. Antalet möjliga rabattkombinationer som måste bedömas överskrider snart vad även en snabb dator kan beräkna och jämföra tillräckligt snabbt för att kunna godtas för butikstransaktioner.

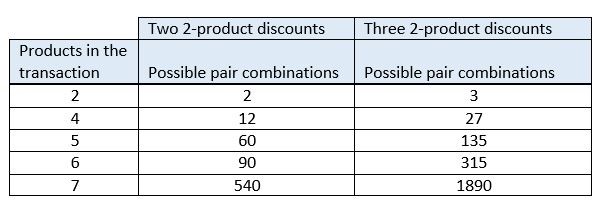
När ännu större kvantiteter eller fler överlappande rabatter används blir det totala antalet möjliga rabattkombinationer snabbt miljontals eller till och med miljarder och den tid som krävs för att utvärdera och välja den bästa möjliga kombinationen blir snabbt betydande. Vissa optimeringar har gjorts i prismotorn för att minska det totala antalet kombinationer som måste utvärderas. Men eftersom antalet överlappande rabatter och kvantiteterna i en transaktion inte är begränsade måste ett stort antal kombinationer alltid utvärderas när det finns överlappande rabatter. Detta är problemet som metoden för marginalvärderankning hanterar.

Marginalvärderankning

För att lösa problemet med ett exponentiellt ökande antal kombinationer som måste utvärderas, finns en optimering som beräknar värdet per delad produkt för varje rabatt i uppsättningen med produkter som två eller flera rabatter kan tillämpas på. Vi kallar detta värde för marginalvärdet på rabatten för de delade produkterna. Marginalvärdet är den genomsnittliga ökningen per produkt av det totala rabattbeloppet när delade produkter tas med i varje rabatt. Marginalvärdet beräknas genom att det totala rabattbeloppet (D_Total), dra av rabattbeloppet utan de delade produkterna (D_{Minus delad}) och dividera denna skillnad med antalet (artiklar_Delad).

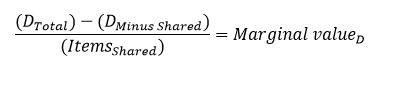
När marginalvärdet av varje rabatt i en delad uppsättning produkter beräknas, tillämpas rabatterna på de delade produkterna i ordning och fullständigt, från högsta marginalvärde till lägsta marginalvärde. För den här metoden jämförs inte alla resterande rabattmöjligheter varje gång när en enda instans av en rabatt har tillämpats. I stället jämförs överlappande rabatter en gång och tillämpas sedan i ordning. Inga ytterligare jämförelser görs. Beräkningen av marginalvärdesordningen utlöses automatiskt när antalet totala möjliga kombinationer överskrider ett fördefinierat tröskelvärde. Den godtagbar tiden att beräkna den totala rabatten varierar mellan butiksbranscher. Tiden ligger dock vanligtvis mellan tiotals millisekunder och en sekund.