Binär klassificering
Klassificering, till exempel regression, är en övervakad maskininlärningsteknik och följer därför samma iterativa process för träning, validering och utvärdering av modeller. I stället för att beräkna numeriska värden som en regressionsmodell beräknar algoritmerna som används för att träna klassificeringsmodeller sannolikhetsvärden för klasstilldelning och de utvärderingsmått som används för att utvärdera modellprestanda jämför de förutsagda klasserna med de faktiska klasserna.
Binära klassificeringsalgoritmer används för att träna en modell som förutsäger en av två möjliga etiketter för en enda klass. I princip förutsäga sant eller falskt. I de flesta verkliga scenarier består de dataobservationer som används för att träna och verifiera modellen av flera funktionsvärden (x) och ett y-värde som antingen är 1 eller 0.
Exempel – binär klassificering
För att förstå hur binär klassificering fungerar ska vi titta på ett förenklat exempel som använder en enda funktion (x) för att förutsäga om etiketten y är 1 eller 0. I det här exemplet använder vi patientens blodsockernivå för att förutsäga om patienten har diabetes eller inte. Här är de data som vi ska träna modellen med:
 |
 |
|---|---|
| Blodsocker (x) | Diabetiker? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Träna en binär klassificeringsmodell
För att träna modellen använder vi en algoritm för att anpassa träningsdata till en funktion som beräknar sannolikheten för att klassetiketten är sann (med andra ord att patienten har diabetes). Sannolikheten mäts som ett värde mellan 0,0 och 1,0, så att den totala sannolikheten för alla möjliga klasser är 1,0. Så till exempel, om sannolikheten för en patient som har diabetes är 0,7, finns det en motsvarande sannolikhet på 0,3 att patienten inte är diabetiker.
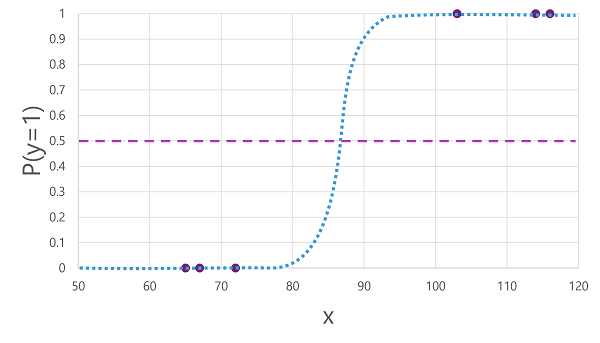
Det finns många algoritmer som kan användas för binär klassificering, till exempel logistisk regression, som härleder en sigmoidfunktion (S-formad) med värden mellan 0,0 och 1,0, så här:
Kommentar
Trots namnet används logistisk regression för maskininlärning för klassificering, inte regression. Den viktiga punkten är den logistiska karaktären hos den funktion som den producerar, som beskriver en S-formad kurva mellan ett lägre och övre värde (0,0 och 1,0 när den används för binär klassificering).
Funktionen som genereras av algoritmen beskriver sannolikheten för att y är sant (y=1) för ett givet värde på x. Matematiskt kan du uttrycka funktionen så här:
f(x) = P(y=1 | x)
För tre av de sex observationerna i träningsdata vet vi att y definitivt är sant, så sannolikheten för de observationer som y = 1 är 1,0 och för de andra tre vet vi att y definitivt är falskt, så sannolikheten att y = 1 är 0,0. Den S-formade kurvan beskriver sannolikhetsfördelningen så att ritning av ett värde på x på raden identifierar motsvarande sannolikhet att y är 1.
Diagrammet innehåller också en vågrät linje som anger det tröskelvärde där en modell baserat på den här funktionen förutsäger sant (1) eller falskt (0). Tröskelvärdet ligger vid mittpunkten för y (P(y) = 0,5). För alla värden vid den här tidpunkten eller senare förutsäger modellen sant (1), medan det för alla värden under den här punkten förutsäger falskt (0). För en patient med en blodsockernivå på 90 skulle funktionen till exempel resultera i ett sannolikhetsvärde på 0,9. Eftersom 0,9 är högre än tröskelvärdet på 0,5 skulle modellen förutsäga sant (1) - med andra ord förutspås patienten ha diabetes.
Utvärdera en binär klassificeringsmodell
Precis som med regression håller du tillbaka en slumpmässig delmängd av data för att verifiera den tränade modellen när du tränar en binär klassificeringsmodell. Anta att vi höll tillbaka följande data för att verifiera vår diabetesklassificerare:
| Blodsocker (x) | Diabetiker? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
Att tillämpa den logistiska funktion som vi härledde tidigare på x-värdena resulterar i följande diagram.
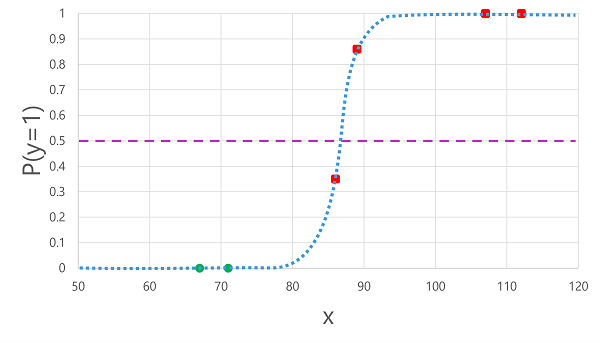
Baserat på om sannolikheten som beräknas av funktionen ligger över eller under tröskelvärdet genererar modellen en förutsagd etikett på 1 eller 0 för varje observation. Vi kan sedan jämföra de förutsagda klassetiketterna (ŷ) med de faktiska klassetiketterna (y), enligt följande:
| Blodsocker (x) | Faktisk diabetesdiagnos (y) | Förutsagd diabetesdiagnos (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Utvärderingsmått för binär klassificering
Det första steget vid beräkning av utvärderingsmått för en binär klassificeringsmodell är vanligtvis att skapa en matris med antalet korrekta och felaktiga förutsägelser för varje möjlig klassetikett:
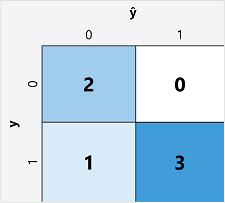
Den här visualiseringen kallas för en förvirringsmatris och visar förutsägelsesummorna där:
- ŷ=0 och y=0: Sanna negativa (TN)
- ŷ=1 och y=0: Falska positiva identifieringar (FP)
- ŷ=0 och y=1: Falska negativa (FN)
- ŷ=1 och y=1: Sanna positiva identifieringar (TP)
Ordningen för förvirringsmatrisen är sådan att korrekta (sanna) förutsägelser visas i en diagonal linje från övre vänstra till nedre högra hörnet. Ofta används färgintensitet för att indikera antalet förutsägelser i varje cell, så en snabb blick på en modell som förutsäger väl bör avslöja en djupt skuggad diagonal trend.
Noggrannhet
Det enklaste måttet som du kan beräkna från förvirringsmatrisen är noggrannhet – andelen förutsägelser som modellen fick rätt. Noggrannhet beräknas som:
(TN+TP) ÷ (TN+FN+FP+TP)
När det gäller vårt diabetesexempel är beräkningen:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Så för våra valideringsdata producerade diabetesklassificeringsmodellen korrekta förutsägelser 83 % av tiden.
Noggrannhet kan till en början verka som ett bra mått för att utvärdera en modell, men tänk på detta. Anta att 11 % av befolkningen har diabetes. Du kan skapa en modell som alltid förutsäger 0, och den skulle uppnå en noggrannhet på 89 %, även om den inte gör några verkliga försök att skilja mellan patienter genom att utvärdera deras funktioner. Vad vi verkligen behöver är en djupare förståelse för hur modellen presterar när det gäller att förutsäga 1 för positiva fall och 0 för negativa fall.
Återkalla
Recall är ett mått som mäter andelen positiva fall som modellen identifierade korrekt. Med andra ord, jämfört med antalet patienter som har diabetes, hur många förutspådde modellen att ha diabetes?
Formeln för återkallande är:
TP-÷ (TP+FN)
För vårt diabetesexempel:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Så vår modell identifierade korrekt 75% av patienterna som har diabetes som har diabetes.
Precision
Precision är ett liknande mått som att återkalla, men mäter andelen förutsagda positiva fall där den sanna etiketten faktiskt är positiv. Med andra ord, vilken andel av patienterna som förutsägs av modellen att ha diabetes har faktiskt diabetes?
Formeln för precision är:
TP-÷ (TP+FP)
För vårt diabetesexempel:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Så 100% av de patienter som förutspås av vår modell att ha diabetes har faktiskt diabetes.
F1-poäng
F1-poäng är ett övergripande mått som kombinerar träffsäkerhet och precision. Formeln för F1-poäng är:
(2 x Precision x recall) ÷ (Precision + träffsäkerhet)
För vårt diabetesexempel:
(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)
= 1,5 ÷ 1,75
= 0,86
Område under kurvan (AUC)
Ett annat namn för återkallande är den sanna positiva frekvensen (TPR), och det finns ett motsvarande mått som kallas falskt positiv frekvens (FPR) som beräknas som FP÷(FP+TN). Vi vet redan att TPR för vår modell när du använder ett tröskelvärde på 0,5 är 0,75, och vi kan använda formeln för FPR för att beräkna värdet 0÷2 = 0.
Om vi skulle ändra tröskelvärdet över vilket modellen förutsäger sant (1) skulle det naturligtvis påverka antalet positiva och negativa förutsägelser och därför ändra TPR- och FPR-måtten. Dessa mått används ofta för att utvärdera en modell genom att rita en ROC-kurva (received operator characteristic ) som jämför TPR och FPR för varje möjligt tröskelvärde mellan 0,0 och 1,0:
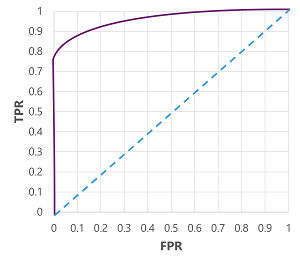
ROC-kurvan för en perfekt modell skulle gå rakt upp på TPR-axeln till vänster och sedan över FPR-axeln längst upp. Eftersom ritytan för kurvan mäter 1x1 skulle området under den här perfekta kurvan vara 1,0 (vilket innebär att modellen är korrekt 100 % av tiden). Däremot representerar en diagonal linje från nedre vänstra hörnet till övre högra hörnet de resultat som skulle uppnås genom att slumpmässigt gissa en binär etikett. producera ett område under kurvan 0,5. Med andra ord kan du med tanke på två möjliga klassetiketter rimligen förvänta dig att gissa rätt 50 % av tiden.
När det gäller vår diabetesmodell produceras kurvan ovan och området under kurvmåttet (AUC) är 0,875. Eftersom AUC är högre än 0,5 kan vi dra slutsatsen att modellen presterar bättre på att förutsäga om en patient har diabetes än att gissa slumpmässigt.