你当前正在访问 Microsoft Azure Global Edition 技术文档网站。 如果需要访问由世纪互联运营的 Microsoft Azure 中国技术文档网站,请访问 https://docs.azure.cn。
本文介绍 T 门和 T 工厂在容错量子计算中的作用。 提供量子算法时,计算运行 T 门和 T 工厂所需的资源对于确定算法的可行性至关重要。 Azure Quantum 资源估算器计算运行算法所需的 T 状态数、单个 T 工厂的物理量子比特数和 T 工厂的运行时。
通用量子门集
根据 DiVincenzo 的标准 ,可缩放的量子计算机必须能够实现一 组通用量子门。 通用集包含执行任何量子计算所需的所有门,即任何计算都必须分解为有限序列的通用门。 至少,量子计算机必须能够将单个量子比特移动到 Bloch Sphere 上的任何位置(使用单量子比特门),并在系统中引入纠缠,这需要多量子比特门。
一台经典计算机上,只有四个可将一个位映射到另一个位的函数。 与此相反,一台量子计算机上,单个量子比特上存在无限数量的幺正变换。 因此,没有有限的基元量子运算或门,可以精确复制量子计算中允许的无限单元转换集。 这意味着,与经典计算不同,量子计算机不可能使用有限数量的门来精确地实现每个可能的量子程序。 所以,量子计算机不可能像经典计算机那样具有通用性。 因此,当我们说一组门对量子计算是通用的时,我们的意思实际上比在经典计算中表达的相关意思稍弱一些。
对于通用性,量子计算机只需要 使用有限长度门序列来近似 有限误差中的每个单一矩阵。
换句话说,如果任何幺正变换都可以近似地写为一组门的乘积,则该门集就是通用的门集。 对于任何规定的错误限制,必须存在入口$G_{1}、G_、\ldots,G_N{2}$入口集,以便
$$ G_N G_{N-1}\cdots G_2 G_1 \approx U。$$
由于矩阵乘法的约定是从右向左乘到此序列中的第一个门运算, $因此G_N$实际上是应用于量子状态向量的最后一个门运算。 更正式地说,如果对于每个容错 $\epsilon>0$ 都存在 $G_1,\ldots, G_N$,使 $G_N\ldots G_1$ 和 $U$ 之间的距离最多为 $\epsilon$,则此类门集是通用的。 理想情况下,达到此 $epsilon$ 距离所需的 $N$ 的值应该通过 $1/\epsilon$ 进行多对数缩放。
例如,由 Hadamard、CNOT 和 T 门构成的集是一个通用集,从中可以生成任何量子计算(在任意数量的量子比特上)。 Hadamard 和 T 门集生成任何单量子比特门:
$$H=\frac{1}{\sqrt{ 1 amp; 1 &\\ amp;-1,T \qquad=\begin{bmatrix} \end{bmatrix}1 & 0 0 &\\ amp; e^{i\pi/4。\end{bmatrix}}&{2}}\begin{bmatrix} $$
在量子计算机中,量子门可以分为两类:克利福德门和非克利福德门,在本例中为 T 门。 仅使用 Clifford 门生成的量子程序可以使用经典计算机高效模拟,因此,需要非克利福德门才能获得量子优势。 在许多量子误差更正(QEC)方案中,所谓的 Clifford 门很容易实现,也就是说,在操作和量子比特方面,它们需要很少的资源来实现容错,而非克利福德门在需要容错时成本很高。 在通用量子门集中,T 门通常用作非克利福德门。
默认包含在 中的 Q#单量子比特 Clifford 门的标准集
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} 、 \qquad S =\begin{bmatrix} 1 & 0 0 &\\ amp; i \end{bmatrix}= T^2、 \qquad X=\begin{bmatrix} 0 &1 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i &\\ amp; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix}0\\ 0&-1 \end{bmatrix}=T^4。 $$
与非克利福德门(T 门)一起,这些操作可以组合成单个量子比特上的任何单一转换。
Azure Quantum 资源估算器中的 T 工厂
非克利福德 T 门准备至关重要,因为其他量子门不足以进行通用量子计算。 若要实现实际缩放算法的非 Clifford 操作,需要低误差率 T 门(或 T 状态)。 但是,它们可能难以直接在逻辑量子比特上实现,并且对于某些物理量子比特也很难实现。
在容错量子计算机中,所需的低误差率 T 状态是使用 T 状态酿酒厂或 T 工厂短时间生成的。 这些 T 工厂通常涉及一系列轮的酿酒,其中每个轮采用以较小的距离代码编码的许多干扰 T 状态,使用提取单元处理它们,并输出在较大距离代码中编码的较少干扰 T 状态,并且轮数、提取单元和距离都是可以变化的参数。 此过程被循环访问,其中一轮的输出 T 状态作为输入馈送到下一轮。
根据 T 工厂的持续时间, Azure Quantum 资源估算器 确定在超过算法总运行时之前可以调用 T 工厂的频率,从而在算法运行时期间生成多少个 T 状态。 通常,所需的 T 状态比算法运行时期间单个 T 工厂调用内生成的状态多。 为了生成更多的 T 状态,资源估算器使用 T 工厂的副本。
T 工厂物理估计
资源估算器计算运行算法所需的 T 状态总数,以及单个 T 工厂及其运行时的物理量子比特数。
目标是在算法运行时中生成所有 T 状态,并尽可能少地复制 T 工厂副本。 下图显示了算法的运行时和一个 T 工厂的运行时的示例。 可以看到 T 工厂的运行时比算法的运行时短。 在此示例中,一个 T 工厂可以提取一个 T 状态。 出现了两个问题:
- T 工厂在算法结束前可以调用多少次?
- 需要多少个 T 工厂提取轮副本来创建算法运行时所需的 T 状态数?
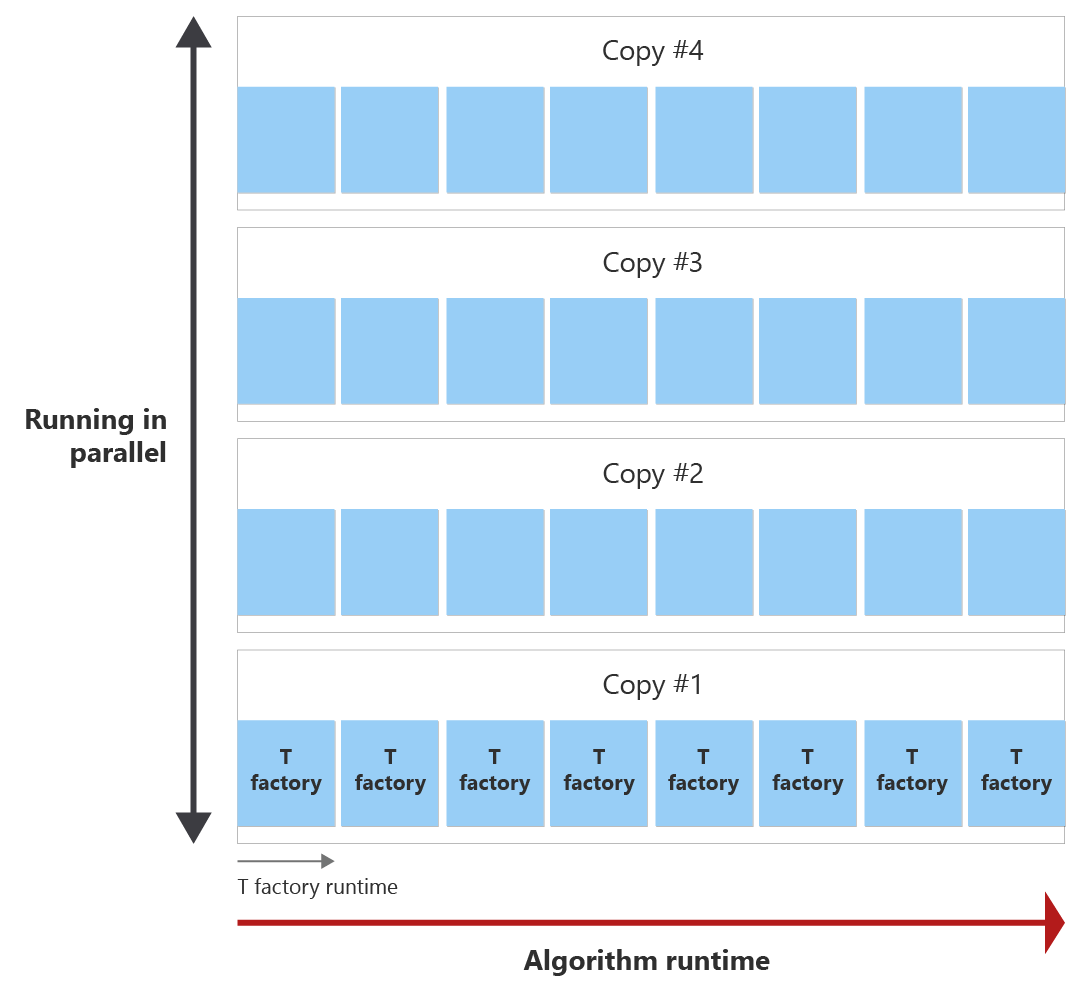
在算法结束之前,可以调用 T 工厂八次,这称为酿酒轮。 例如,如果需要 30 个 T 状态,则会在算法运行时调用单个 T 工厂 8 次,从而创建 8 个 T 状态。 然后,需要四份 T 工厂酿酒轮并行运行,以提取所需的 30 个 T 状态。
注意
请注意,T 工厂副本和 T 工厂调用不同。
T 状态酿酒厂采用一系列轮实现,其中每轮由一组并行运行的酿酒单元副本组成。 资源估算器计算运行一个 T 工厂所需的物理量子比特数,以及 T 工厂的运行时间以及其他必需参数。
只能对 T 工厂执行完全调用。 因此,在某些情况下,所有 T 工厂调用的累积运行时小于算法运行时。 由于量子比特被不同的舍入重复使用,因此一个 T 工厂的物理量子比特数是用于一轮的物理量子比特的最大数量。 T 工厂的运行时是四舍五入的运行时总和。
注意
如果物理 T 门错误率低于所需的逻辑 T 状态错误率,则资源估算器无法执行良好的资源估计。 提交资源估算作业时,可能会遇到无法找到 T 工厂,因为所需的逻辑 T 状态错误率太低或太高。
有关详细信息,请参阅“评估要求以缩放到实际量子优势”的附录 C。