使用语言集成查询 (LINQ)

介绍

本教程介绍 .NET 和 C# 语言中的功能。你将学会如何：

使用 LINQ 生成序列。
编写可在 LINQ 查询中轻松使用的方法。
区分及早计算和惰性计算。

通过开发一个演示魔术师基本技能之一——法罗洗牌的应用程序，你可以学习这些技术。法罗洗牌是一种技术，你可以将一副纸牌完全拆分成两半，然后每张牌交错插入，以重建原始牌堆。

魔术师使用此技术，因为每个卡片在每次洗牌后都位于一个已知位置，并且顺序是重复模式。

本教程以轻松的方式看待操控数据序列的过程。应用程序构造卡片组，执行一系列随机排列，并每次将序列写出。它还将更新的顺序与原始订单进行比较。

本教程包含多个步骤。执行每个步骤后，可以运行应用程序并查看进度。还可以在 dotnet/samples GitHub 存储库中看到已完成的示例。有关下载说明，请参阅示例和教程。

先决条件

创建应用程序

创建新的应用程序。打开命令提示符并为应用程序创建新目录。使该目录成为当前目录。在命令提示符处键入命令 dotnet new console -o LinqFaroShuffle。此命令为基本的“Hello World”应用程序创建初始文件。

如果以前从未使用过 C# ，本教程说明 C# 程序的结构。你可以阅读该内容，然后返回此处了解有关 LINQ 的详细信息。

创建数据集

小窍门

在本教程中，可以在调用 LinqFaroShuffle 的命名空间中组织代码以匹配示例代码，也可以使用默认的全局命名空间。如果选择使用命名空间，请确保所有类和方法都在同一命名空间中一致，或根据需要添加适当的 using 语句。

请思考纸牌的构成元素。一副扑克牌有四种花色，每种花色有13个点数。通常，可以考虑立即创建一个 Card 类，并手动填充对象的集合 Card 。使用 LINQ，可以比通常创建一副纸牌的方式更简洁。而不是创建类，而是创建两个 Card 序列来表示西装和排名。创建一对 迭代器方法 ，以字符串形式生成排名和花色：

static IEnumerable<string> Suits()
{
    yield return "clubs";
    yield return "diamonds";
    yield return "hearts";
    yield return "spades";
}

static IEnumerable<string> Ranks()
{
    yield return "two";
    yield return "three";
    yield return "four";
    yield return "five";
    yield return "six";
    yield return "seven";
    yield return "eight";
    yield return "nine";
    yield return "ten";
    yield return "jack";
    yield return "queen";
    yield return "king";
    yield return "ace";
}

请将这些方法放置在你的 Program.cs 文件中，位于 Console.WriteLine 语句之下。这两种方法都使用 yield return 语法在运行时生成序列。编译器生成一个对象，该对象在请求时实现 IEnumerable<T> 并生成字符串序列。

现在，使用这些迭代器方法创建一组卡片。将 LINQ 查询置于文件的顶部 Program.cs 。如下所示：

var startingDeck = from s in Suits()
                   from r in Ranks()
                   select (Suit: s, Rank: r);

// Display each card that's generated and placed in startingDeck
foreach (var card in startingDeck)
{
    Console.WriteLine(card);
}

多个 from 子句生成 SelectMany，用于将第一个和第二个序列中的所有元素合并成一个序列。顺序对于此示例很重要。第一个源序列中的第一个元素（Suits）与第二个序列（Ranks）中的每个元素组合在一起。此过程生成所有 13 张第一套卡。对第一个序列（花色）中的每个元素重复此过程。最后生成按花色排序（后跟值）的一副纸牌。

请记住，无论是在前面的示例中使用的查询语法中编写 LINQ 还是改用方法语法，始终可以从一种语法形式到另一种语法。以查询语法编写的上述查询可以用方法语法编写为：

var startingDeck = Suits().SelectMany(suit => Ranks().Select(rank => (Suit: suit, Rank: rank )));

编译器将使用查询语法编写的 LINQ 语句转换为等效的方法调用语法。因此，无论选择哪种语法，查询的两个版本都会生成相同的结果。选择最适合你的情况的语法。例如，如果你在一个团队中工作，其中某些成员难以使用方法语法，请尝试使用查询语法。

运行此时生成的示例。它显示牌组中所有52张扑克牌。你可能会发现，在调试器下运行这个示例有助于观察Suits()和Ranks()方法的执行过程。可以清楚地看到，每个序列中的每个字符串仅根据需要生成。

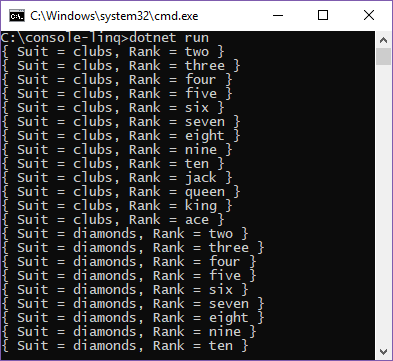
显示应用写出 52 张卡片的控制台窗口。

调整顺序

接下来，专注于如何洗牌牌组。任何成功洗牌的第一步是将牌组分成两部分。 Take 方法和 Skip 方法是 LINQ API 的一部分，它们提供了该功能。请将它们放在foreach循环之后：

var top = startingDeck.Take(26);
var bottom = startingDeck.Skip(26);

不过，标准库中没有可用的 shuffle 方法，因此您需要编写自己的 shuffle 方法。你创建的洗牌方法展示了几种在 LINQ 程序中使用的技术，因此该过程的每一步都进行了详细的说明。

若要将功能添加到与 IEnumerable<T> LINQ 查询结果交互的方式，请编写一些称为扩展方法的特殊方法。扩展方法是一种特殊用途 的静态方法 ，可将新功能添加到已存在的类型，而无需修改要向其添加功能的原始类型。

向程序添加新的静态类文件（名称为），以用于存放扩展方法，然后开始生成第一个扩展方法：Extensions.cs

public static class CardExtensions
{
    extension<T>(IEnumerable<T> sequence)
    {
        public IEnumerable<T> InterleaveSequenceWith(IEnumerable<T> second)
        {
            // Your implementation goes here
            return default;
        }
    }
}

注释

如果使用 Visual Studio 以外的编辑器（如 Visual Studio Code），可能需要添加到using LinqFaroShuffle;Program.cs文件的顶部，以便可访问扩展方法。 Visual Studio 会自动添加此 using 语句，但其他编辑器可能不是。

容器 extension 指定要扩展的类型。节点extension为容器中的所有成员声明extension的类型和名称。在此示例中，你将进行扩展 IEnumerable<T>，并命名 sequence参数。

扩展成员声明看起来就像是接收器类型的成员：

public IEnumerable<T> InterleaveSequenceWith(IEnumerable<T> second)

调用该方法，就像它是扩展类型的成员方法一样。此方法声明还遵循一个标准惯例，其中输入和输出类型为 IEnumerable<T>。这种做法使 LINQ 方法可以链接在一起来执行更复杂的查询。

由于你把甲板分成了一半，你需要把这两半合并在一起。在代码中，这意味着同时枚举通过 Take 和 Skip 获取的两个序列，将元素交错整合，并创建一个序列：即您现在的洗牌结果。编写适用于两个序列的 LINQ 方法需要你了解 IEnumerable<T> 的工作原理。

IEnumerable<T> 接口有一个方法 (GetEnumerator)。返回的 GetEnumerator 对象具有一个方法用于移到下一个元素，还有一个属性用于检索序列中的当前元素。使用这两个成员枚举集合并返回元素。此 Interleave 方法是一种迭代器方法，因此，与其生成并返回集合，不如使用前面代码中所示的 `yield return` 语法。

下面是该方法的实现：

public IEnumerable<T> InterleaveSequenceWith(IEnumerable<T> second)
{
    var firstIter = sequence.GetEnumerator();
    var secondIter = second.GetEnumerator();

    while (firstIter.MoveNext() && secondIter.MoveNext())
    {
        yield return firstIter.Current;
        yield return secondIter.Current;
    }
}

现在你编写了此方法，请返回到该方法 Main 并洗牌一次：

var shuffledDeck = top.InterleaveSequenceWith(bottom);

foreach (var c in shuffledDeck)
{
    Console.WriteLine(c);
}

比较

确定将牌组重新设置为其原始顺序需要多少次洗牌。若要了解情况，请编写一个确定两个序列是否相等的方法。在您获得该方法后，将洗牌的代码置于循环中，并检查何时牌堆恢复原始顺序。

编写方法以确定这两个序列是否相等应该很简单。这是一个与你编写的洗牌方法类似的结构。但是，这次，而不是对每个元素使用 yield return ，而是比较每个序列的匹配元素。枚举整个序列时，如果每个元素都匹配，则序列相同：

public bool SequenceEquals(IEnumerable<T> second)
{
    var firstIter = sequence.GetEnumerator();
    var secondIter = second.GetEnumerator();

    while ((firstIter?.MoveNext() == true) && secondIter.MoveNext())
    {
        if ((firstIter.Current is not null) && !firstIter.Current.Equals(secondIter.Current))
        {
            return false;
        }
    }

    return true;
}

此方法显示第二个 LINQ 成语：终端方法。它们采用序列作为输入（在本例中为两个序列），并返回单个标量值。使用终端方法时，它们始终是 LINQ 查询方法链中的最终方法。

当你使用它来确定牌组何时恢复到原始顺序时，可以看到这种情况的发生。将洗牌代码放入循环中，并在通过应用 SequenceEquals() 方法使序列恢复其原始顺序时停止。可以看到它始终是任何查询中的最终方法，因为它返回单个值而不是序列：

var startingDeck = from s in Suits()
                   from r in Ranks()
                   select (Suit: s, Rank: r);

// Display each card generated and placed in startingDeck in the console
foreach (var card in startingDeck)
{
    Console.WriteLine(card);
}

var top = startingDeck.Take(26);
var bottom = startingDeck.Skip(26);

var shuffledDeck = top.InterleaveSequenceWith(bottom);

var times = 0;
// Re-use the shuffle variable from earlier, or you can make a new one
shuffledDeck = startingDeck;
do
{
    shuffledDeck = shuffledDeck.Take(26).InterleaveSequenceWith(shuffledDeck.Skip(26));

    foreach (var card in shuffledDeck)
    {
        Console.WriteLine(card);
    }
    Console.WriteLine();
    times++;

} while (!startingDeck.SequenceEquals(shuffledDeck));

Console.WriteLine(times);

运行你编写的代码，然后注意牌组在每次洗牌后如何重新排列。进行 8 次洗牌后（迭代 do-while 循环），扑克牌恢复从最初的 LINQ 查询首次创建它时的原始配置。

优化

到目前为止你构建的示例执行一个外洗牌，其中顶部和底部的卡片在每次运行中保持不变。让我们进行一个更改：改用随机卡片，其中所有 52 张卡片更改位置。向内洗牌是指，交错一副纸牌时，将后一半中的第一张纸牌变成一副纸牌中的第一张纸牌。也就是说，上半部分中的最后一张纸牌变成一副纸牌中的最后一张纸牌。此更改需要一行代码。交换 Take 和 Skip 的位置，来更新当前洗牌查询。此更改将切换甲板顶部和下半部分的顺序：

shuffledDeck = shuffledDeck.Skip(26).InterleaveSequenceWith(shuffledDeck.Take(26));

再次运行程序，你可以看到牌组重新排序需要 52 次迭代。当程序持续运行时，您还会注意到一些严重的性能下降。

此性能下降有几个原因。可以解决以下主要原因之一： 延迟评估的使用效率低下。

延迟计算指出，在需要语句的值之前，不会执行该语句的求值。 LINQ 查询属于延迟计算的语句。仅当请求元素时，才会生成序列。通常，这是 LINQ 的主要优势。但是，在这样的程序中，延迟计算会导致执行时间呈指数增长。

请记住，你使用 LINQ 查询生成了原始甲板。每次洗牌都是通过对上一副牌组执行三个 LINQ 查询生成的。所有这些查询都是惰性执行的。这也意味着每次请求序列时，它们会被再次执行。到达第 52 次迭代时，已经多次重新生成原始牌组。编写日志来演示此行为。收集数据后，可以提高性能。

在Extensions.cs文件中，输入或复制以下代码示例中的方法。此扩展方法在项目目录中创建名为 debug.log 的新文件，并记录当前正在对日志文件执行的查询。将此扩展方法追加到任何查询，以标记该查询已执行。

public IEnumerable<T> LogQuery(string tag)
{
    // File.AppendText creates a new file if the file doesn't exist.
    using (var writer = File.AppendText("debug.log"))
    {
        writer.WriteLine($"Executing Query {tag}");
    }

    return sequence;
}

接下来，使用日志消息检测每个查询的定义：

var startingDeck = (from s in Suits().LogQuery("Suit Generation")
                    from r in Ranks().LogQuery("Rank Generation")
                    select (Suit: s, Rank: r)).LogQuery("Starting Deck");

foreach (var c in startingDeck)
{
    Console.WriteLine(c);
}

Console.WriteLine();
var times = 0;
var shuffle = startingDeck;

do
{
    // Out shuffle
    /*
    shuffle = shuffle.Take(26)
        .LogQuery("Top Half")
        .InterleaveSequenceWith(shuffle.Skip(26)
        .LogQuery("Bottom Half"))
        .LogQuery("Shuffle");
    */

    // In shuffle
    shuffle = shuffle.Skip(26).LogQuery("Bottom Half")
            .InterleaveSequenceWith(shuffle.Take(26).LogQuery("Top Half"))
            .LogQuery("Shuffle");

    foreach (var c in shuffle)
    {
        Console.WriteLine(c);
    }

    times++;
    Console.WriteLine(times);
} while (!startingDeck.SequenceEquals(shuffle));

Console.WriteLine(times);

请注意，不是每次访问查询都会生成日志。只有在创建原始查询时，才会生成日志。程序仍需要很长时间才能运行，但现在可以看到原因。如果对在启用日志记录的情况下运行向内洗牌失去了耐心，请切换回向外洗牌。你仍然看到惰性求值的影响。在一次运行中，它会执行 2,592 个查询，包括数值和牌型生成。

可以改进代码的性能，以减少所执行的次数。一个简单的解决方法是缓存构建卡片组的原始 LINQ 查询的结果。目前，每次 do-while 循环迭代时，你会反复执行查询，重新构造牌组并洗牌。若要缓存卡片组，请应用 LINQ 方法 ToArray 和 ToList。将它们追加到查询时，它们会执行你指定的相同操作，但现在它们会将结果存储在数组或列表中，这取决于你选择调用的方法。将 LINQ 方法 ToArray 追加到查询并再次运行程序：

var startingDeck = (from s in suits().LogQuery("Suit Generation")
                    from r in ranks().LogQuery("Value Generation")
                    select new { Suit = s, Rank = r })
                    .LogQuery("Starting Deck")
                    .ToArray();

foreach (var c in startingDeck)
{
    Console.WriteLine(c);
}

Console.WriteLine();

var times = 0;
var shuffle = startingDeck;

do
{
    /*
    shuffle = shuffle.Take(26)
        .LogQuery("Top Half")
        .InterleaveSequenceWith(shuffle.Skip(26).LogQuery("Bottom Half"))
        .LogQuery("Shuffle")
        .ToArray();
    */

    shuffle = shuffle.Skip(26)
        .LogQuery("Bottom Half")
        .InterleaveSequenceWith(shuffle.Take(26).LogQuery("Top Half"))
        .LogQuery("Shuffle")
        .ToArray();

    foreach (var c in shuffle)
    {
        Console.WriteLine(c);
    }

    times++;
    Console.WriteLine(times);
} while (!startingDeck.SequenceEquals(shuffle));

Console.WriteLine(times);

现在向外洗牌下降到 30 次查询。再次使用“in shuffle”运行，你会看到类似的改进：它现在执行 162 个查询。

此示例旨在突出显示延迟评估可能导致性能困难的用例。了解延迟计算会在何处影响代码性能至关重要，但了解并非所有查询应及早运行也同等重要。不使用 ToArray 会对性能产生影响，因为每副牌的新排列都是基于以前的排列方式生成的。使用惰性计算意味着一副纸牌的每个新配置都以原来的一副纸牌为依据，甚至在执行生成 startingDeck 的代码时，也不例外。这会导致大量的额外工作。

在实践中，某些算法在急切求值的情况下运行良好，而另一些在惰性求值的情况下运行良好。对于日常使用，当数据源是单独的进程（如数据库引擎）时，惰性求值通常是更好的选择。对于数据库，使用延迟计算，更复杂的查询可以只对数据库进程执行一次往返，然后返回至剩余的代码。无论选择使用惰性评估还是急切评估，LINQ 都是灵活的，因此请衡量流程并选取哪种评估为你提供最佳性能。

结论

在此项目中，你介绍了：

使用 LINQ 查询将数据聚合为有意义的序列。
编写扩展方法以向 LINQ 查询添加自定义功能。
在代码中查找 LINQ 查询可能会遇到性能问题（如速度下降）的区域。
LINQ 查询中的延迟和急切评估及其对查询性能的影响。

除了 LINQ，你还了解了魔术师用于卡片技巧的技术。魔术师使用法罗洗牌，因为他们可以控制每张牌在牌组中的位置。既然你已经知道了，就不要透露给其他人！

有关 LINQ 的详细信息，请参阅：

反馈

此页面是否有帮助？

Last updated on 2025-12-02