使用变换矩阵的第三列创建透视和锥形效果
平移、缩放、旋转和倾斜都属于仿射变换。 仿射变换保留平行线。 如果两条线在变换之前平行,则它们在变换之后仍保持平行。 矩形始终变换为平行四边形。
但是,SkiaSharp 还能够进行非仿射变换,可将矩形变换为任何凸四边形:

凸四边形是内角始终小于 180 度且边不互相交叉的四边形。
当变换矩阵的第三行设置为 0、0 和 1 以外的值时,会产生非仿射变换。 完整的 SKMatrix 乘法为:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
最终的变换公式为:
x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z` = Persp0·x + Persp1·y + Persp2
使用 3×3 矩阵进行二维变换的基本规则是所有内容都保留在 Z 等于 1 的平面上。 除非 Persp0 和 Persp1 为 0,且 Persp2 等于 1,否则变换会将 Z 坐标移离该平面。
若要将其还原为二维变换,必须将坐标移回该平面。 还需要执行另一个步骤。 x'、y' 和 z` 值必须除以 z':
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
这些称为齐次坐标,由数学家 August Ferdinand Möbius 提出,Möbius 因他的拓扑奇观“Möbius 带”而知名。
如果 z' 为 0,则除法结果为无限坐标。 事实上,Möbius 开发齐次坐标的动机之一是能够用有限的数字表示无限值。
但是,在显示图形时,建议你避免渲染其坐标会变换为无限值的内容。 这些坐标不会渲染。 这些坐标附近的所有内容将非常大,并且可能在视觉上不连贯。
在此等式中,你不希望 z' 的值变为零:
z` = Persp0·x + Persp1·y + Persp2
因此,这些值存在一些实际限制:
Persp2 单元格可为零,也可以不为零。 如果 Persp2 为零,则点 (0, 0) 的 z' 为零,这通常是不可取的,因为该点在二维图形中非常常见。 如果 Persp2 不等于 0,则将 Persp2 固定为 1 也不会丢失泛性。 例如,如果确定 Persp2 应为 5,则你只需将矩阵中的所有单元格除以 5,这使得 Persp2 等于 1,而结果是相同的。
由于这些原因,Persp2 通常固定为 1,这与标识矩阵中的值相同。
通常,Persp0 和 Persp1 是小数字。 例如,假设从标识矩阵开始,但将 Persp0 设置为 0.01:
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
变换公式为:
x` = x / (0.01·x + 1)
y' = y / (0.01·x + 1)
现在使用此变换来渲染位于原点处的 100 像素方框。 下面是四个角的变换方式:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
当 x 为 100 时,z' 分母为 2,因此 x 和 y 坐标实际上会减半。 框的右侧变得比左侧短:
这些单元格名称的 Persp 部分指的是“透视”,因为透视缩短表明该框现在倾斜,右侧距离观察者更远。
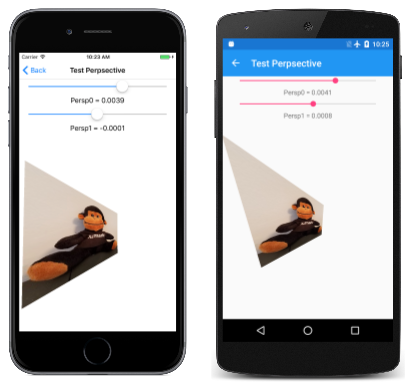
在“测试透视”页中,可以试验 Persp0 和 Pers1 的值,以了解它们的工作原理。 这些矩阵单元格的合理值非常小,以至于通用 Windows 平台中的 Slider 无法正确处理它们。 为了解决 UWP 问题,需要将 TestPerspective.xaml 中的两个 Slider 元素初始化为 –1 到 1 的范围:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
TestPerspectivePage 代码隐藏文件中滑块的事件处理程序将值除以 100,使其范围介于 –0.01 和 0.01 之间。 此外,构造函数加载位图:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
PaintSurface 处理程序根据这两个滑块的值除以 100 来计算名为 perspectiveMatrix 的 SKMatrix 值。 它与两个平移变换相结合,将变换的中心置于位图的中心:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
下面是一些示例图像:
在试验滑块时,你会发现超过 0.0066 或低于 –0.0066 的值会导致图像突然变得破碎且不连贯。 正在变换的位图是 300 像素的正方形。 它相对于其中心进行变换,因此位图的坐标范围为 –150 到 150。 回想一下,z' 的值为:
z` = Persp0·x + Persp1·y + 1
如果 Persp0 或 Persp1 大于 0.0066 或小于 –0.0066,则位图的某个坐标始终会导致 z' 值为零。 这会导致除以零,使渲染内容变得一团糟。 使用非仿射变换时,建议避免渲染其坐标会导致除以零的任何内容。
通常,你不会单独设置 Persp0 和 Persp1。 通常还需要在矩阵中设置其他单元以实现某些类型的非仿射变换。
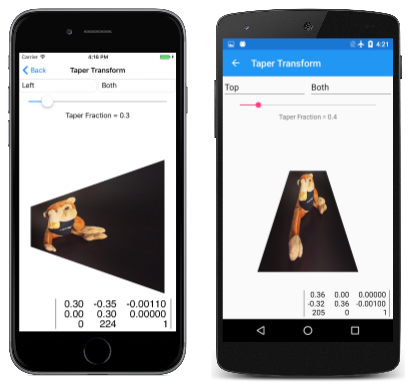
此类非仿射变换之一是锥形变换。 这种类型的非仿射变换保留了矩形的整体大小,但一侧逐渐变细:
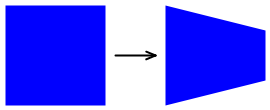
TaperTransform 类基于以下参数执行非仿射变换的广义计算:
- 正在变换的图像的矩形大小;
- 一个指示渐缩矩形边的枚举;
- 另一个指示它如何逐渐变细的枚举,以及
- 逐渐变细的程度。
下面是 代码:
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
此类在“锥形变换”页中使用。 XAML 文件实例化两个 Picker 元素来选择枚举值,并实例化一个 Slider 来选择锥度分数。 PaintSurface 处理程序将锥形变换与两个平移变换相结合,使变换相对于位图的左上角:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
以下是一些示例:
另一种广义非仿射变换是 3D 旋转,下一篇文章 3D 旋转将对此进行演示。
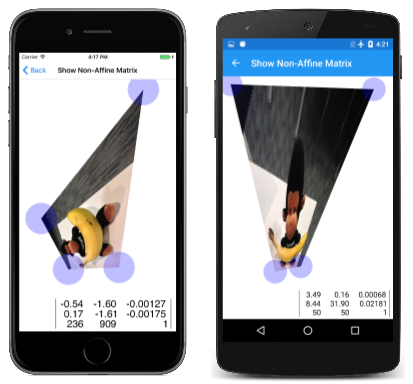
非仿射变换可以将矩形变换为任意凸四边形。 “显示非仿射矩阵”页对此进行了演示。 它与矩阵变换一文中的“显示仿射矩阵”页非常相似,不同之处在于它有第四个 TouchPoint 对象来操控位图的第四个角:
只要你不尝试使位图一个角的内角大于 180 度,或使两条边相交,程序就会使用 ShowNonAffineMatrixPage 类中的此方法成功计算变换:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
为了便于计算,此方法将总变换获取为三个单独变换的乘积,此处用箭头进行符号化,显示这些变换如何修改位图的四个角:
(0, 0) → (0, 0) → (0, 0) → (x0, y0)(左上)
(0, H) → (0, 1) → (0, 1) → (x1, y1)(左下)
(W, 0) → (1, 0) → (1, 0) → (x2, y2)(右上)
(W, H) → (1, 1) → (a, b) → (x3, y3)(右下)
右侧的最终坐标是与四个触摸点关联的四个点。 这些是位图角的最终坐标。
W 和 H 表示位图的宽度和高度。 第一个变换 S 只是将位图缩放为 1 像素的正方形。 第二个变换是非仿射变换 N,第三个变换是仿射变换 A。 该仿射变换基于三个点,因此它就像早期的仿射 ComputeMatrix 方法一样,并且不涉及包含 (a, b) 点的第四行。
计算 a 和 b 值,使第三个变换成为仿射变换。 该代码获取仿射变换的逆变换,然后使用它来映射右下角。 该位置就是点 (a, b)。
非仿射变换的另一个用途是模仿三维图形。 下一篇文章 3D 旋转将介绍如何在 3D 空间中旋转二维图形。