二元分类
注释
有关更多详细信息,请参阅 “文本和图像 ”选项卡!
分类(如回归)是 一种受监督的 机器学习技术:因此,遵循训练、验证和评估模型相同的迭代过程。 用于训练分类模型的算法而不是计算回归模型等数值,而是计算类赋值的 概率 值,以及用于评估模型性能的计算指标,将预测类与实际类进行比较。
二元分类 算法用于训练一个模型,该模型预测单个类的两个可能标签之一。 本质上,预测 true 或 false。 在大多数实际方案中,用于训练和验证模型的数据观察由多个特征(x)值和 y 值组成,该值为 1 或 0。
示例 - 二元分类
为了了解二元分类的工作原理,让我们看看使用单个特征(x)来预测标签 y 是 1 还是 0 的简化示例。 在此示例中,我们将使用患者的血糖水平来预测患者是否患有糖尿病。 这是我们用来训练模型的数据:

|

|
|---|---|
| 血糖 (x) | 糖尿病患者? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
训练二元分类模型
为了训练模型,我们将使用算法将训练数据拟合到一个函数中,该函数计算类标签为 true 的概率(换句话说,患者患有糖尿病)。 概率测量为介于 0.0 和 1.0 之间的值,以便所有可能的类的总概率为 1.0。 因此,例如,如果患者患有糖尿病的概率为 0.7,那么患者没有糖尿病的相应概率为 0.3。
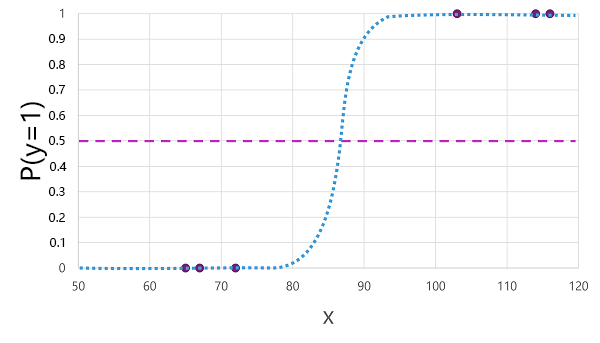
有许多算法可用于二元分类,例如 逻辑回归,该算法派生的 sigmoid (S 形)函数的值介于 0.0 和 1.0 之间,如下所示:
注释
尽管它的名称,但在机器学习 逻辑回归 中用于分类,而不是回归。 要点是它生成的函数的 逻辑 性质,它描述用于二元分类时的低值和上限值之间的 S 形曲线(0.0 和 1.0)。
算法生成的函数描述给定值为 x 的 y 为 true(y=1)的概率。 从数学上看,可以像这样表达函数:
f(x) = P(y=1 | x)
对于训练数据中的六个观测值中的三个,我们知道 y 肯定为 true,因此这些观测值使 y=1 的概率为 1.0。对于其他三个,我们知道 y 肯定为 false,因此这些观测值使 y=1 的概率为 0.0。 S 形曲线描述概率分布,以便绘制线条上的 x 值可识别 y 为 1 的相应概率。
该图还包含一条水平线,用于指示基于此函数的模型预测 true (1) 或 false (0) 的阈值。 阈值位于 y (P(y) = 0.5 的中间点。 对于此时或更高点的任何值,模型将预测 true (1):虽然对于低于此点的任何值,它将预测 false (0)。 例如,对于血糖水平为 90 的患者,该函数的概率值为 0.9。 由于 0.9 高于 0.5 的阈值,因此模型将预测 为 true (1), 换句话说,预测患者患有糖尿病。
评估二元分类模型
与回归一样,在训练二元分类模型时,可以保留一个随机的数据子集,用于验证已训练的模型。 假设我们保留以下数据来验证糖尿病分类器:
| 血糖 (x) | 糖尿病患者? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
将之前派生的逻辑函数应用于 x 值会导致以下绘图。
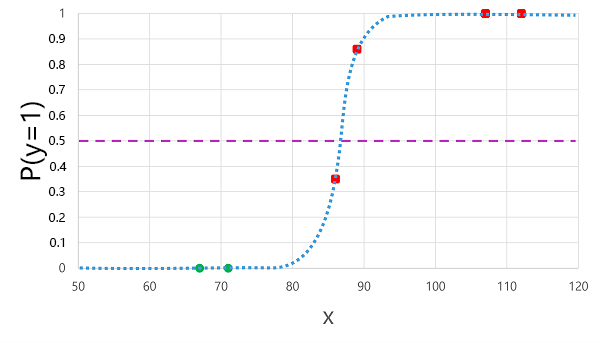
根据函数计算的概率是否高于或低于阈值,模型为每个观察生成 1 或 0 的预测标签。 然后,我们可以将 预测 的类标签(ŷ)与 实际 类标签(y)进行比较,如下所示:
| 血糖 (x) | 实际的糖尿病诊断 (y) | 预测的糖尿病诊断 (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
二元分类评估指标
计算二元分类模型的评估指标的第一步通常是为每个可能的类标签创建正确和不正确的预测数的矩阵:
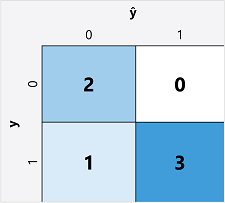
此可视化效果称为 混淆矩阵,它显示预测总计,其中:
- ŷ=0 和 y=0: 真负数 (TN)
- ŷ=1 和 y=0: 假阳性 (FP)
- ŷ=0 和 y=1: 假负 (FN)
- ŷ=1 且 y=1:真正 (TP)
混淆矩阵的排列方式使得正确的(true)预测显示在从左上到右下角的对角线中。 通常,颜色的强度用于表示每个单元格中预测的数量,因此快速浏览一个预测良好的模型会显示出深色的对角线趋势。
准确性
从混淆矩阵中计算的最简单指标是 准确性 - 模型正确预测的比例。 准确性计算为:
(TN+TP) ÷ (TN+FN+FP+TP)
在我们的糖尿病示例中,计算为:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
因此,就我们的验证数据来说,糖尿病分类模型在 83% 的情况下产生正确的预测。
准确性最初似乎是一个很好的指标来评估模型,但请考虑这一点。 假设11% 的人口患有糖尿病。 你可以创建一个始终预测 0 的模型,并且它将实现 89%的准确性,即使它并没有真正尝试通过评估患者的特征来区分患者。 我们真正需要的是更深入地了解模型在预测正事例 1 时的表现,以及 0 对负事例的预测。
召回率
召回 率是衡量模型正确识别的积极事例比例的指标。 换句话说,与 患有 糖尿病的患者数量相比,模型 预测 患有糖尿病的人数是多少?
召回公式为:
TP ÷ (TP+FN)
对于我们的糖尿病示例:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
因此,我们的模型正确地将 75% 的糖尿病患者识别为糖尿病患者。
精准率
精准率是与召回率类似的指标,但度量的是预测为阳性病例且真实标签实际上也为阳性的比例。 换句话说,模型 预测 的糖尿病患者实际 患有 糖尿病的比例是多少?
精度公式为:
TP ÷ (TP+FP)
对于我们的糖尿病示例:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
因此,在我们的模型预测的患有糖尿病的患者中,100% 的人确实患有糖尿病。
F1 分数
F1 分数 是组合召回率和精度的总体指标。 F1 分数的公式为:
(2 x 精确率 x 召回率) ÷ (精确率 + 召回率)
对于我们的糖尿病示例:
(2 x 1.0 x 0.75) ÷ (1.0 + 0.75)
= 1.5 ÷ 1.75
= 0.86
曲线下面积 (AUC)
召回的另一个名称是真正的正率(TPR),有一个等效的指标称为误报率(FPR),计算为 FP÷(FP+TN)。 我们已经知道,当使用 0.5 的阈值时,我们模型的 TPR 为 0.75,并且我们可以使用 FPR 的公式来计算得出 (0 ÷ 2) = 0 的值。
当然,如果我们要更改模型预测 true(1)的阈值,它将影响正预测和负预测的数量,因此更改 TPR 和 FPR 的指标。 这些指标通常用于通过绘制 接收的运算符特征 (ROC) 曲线来评估模型,该曲线比较了 0.0 和 1.0 之间的每个可能的阈值的 TPR 和 FPR:
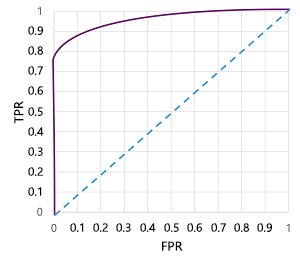
完美模型的 ROC 曲线将直线上升到左侧的 TPR 轴,然后在顶部穿过 FPR 轴。 由于曲线的绘图面积为 1x1,因此该完美曲线下的面积将为 1.0(这意味着模型始终是正确的)。 相比之下,从左下到右上方的对角线表示通过随机猜测二进制标签实现的结果:生成 0.5 曲线下的区域。 换句话说,给定两个可能的类标签,你可以合理预期猜对的概率为 50%。
对于我们的糖尿病模型,将生成上述 曲线,曲线( AUC)指标下的面积为 0.875。 由于 AUC 高于 0.5,因此我们可以得出结论,模型在预测患者是否患有糖尿病比随机猜测时表现更好。