多类分类
多类分类 用于预测观测所属的多个可能类中的哪一个。 作为监督式机器学习技术，它遵循与回归和二元分类相同的迭代 训练、验证和评估 过程，其中训练数据的子集被保留以验证训练的模型。
示例 - 多类分类
用于计算多个类标签概率值的多类分类算法，使模型能够预测给定观察的最可能的类。
让我们探讨一个示例，其中我们对企鹅进行了一些观察，其中记录了每个企鹅的翻转器长度（x）。 对于每个观察，数据包括企鹅物种（y），编码如下：
- 0： Adelie
- 1：根图
- 2：帽带企鹅
注释
与本模块前面的示例一样，实际方案将包含多个功能 （x） 值。 我们将使用一个特性以简化过程。
|
|
|---|---|
| 翻转器长度 （x） | 物种 （y） |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
训练多类分类模型
若要训练多类分类模型，我们需要使用算法将训练数据拟合到计算每个可能类的概率值的函数。 有两种类型的算法可用于执行此作：
- 一对其他 (OvR) 算法
- 多项式算法
一对其他 (OvR) 算法
一对其他算法为每个类训练一个二元分类函数，每个函数计算观察结果属于目标类示例的概率。 与 任何其他 类相比，每个函数计算观察结果是特定类的概率。 对于企鹅物种分类模型，算法实质上将创建三个二元分类函数：
- f0（x） = P（y=0 | x）
- f1（x） = P（y=1 | x）
- f2（x） = P（y=2 | x）
每个算法生成一个 sigmoid 函数，用于计算介于 0.0 和 1.0 之间的概率值。 使用此类算法训练的模型预测生成最高概率输出的函数的类。
多项式算法
另一种方法是使用多项式算法，该算法创建返回多值输出的单个函数。 输出是一个 矢量 （一个值数组），其中包含所有可能的类的 概率分布 - 每个类的概率分数，当总计高达 1.0 时：
f（x） =[P（y=0|x）， P（y=1|x）， P（y=2|x）]
此类函数的示例是 softmax 函数，它可以生成如下示例所示的输出：
[0.2, 0.3, 0.5]
矢量中的元素分别表示类 0、1 和 2 的概率：因此，在这种情况下，概率最高的类为 2。
无论使用哪种类型的算法，模型都使用生成的函数来确定给定特征集（x）的最可能类，并预测相应的类标签（y）。
评估多类分类模型
可以通过计算每个类的二元分类指标来评估多类分类器。 或者，可以计算将所有类考虑在内的总指标。
假设我们已经验证了多类分类器，并获得了以下结果：
| 翻转器长度 （x） | 实际物种 (y) | 预测物种 (ŷ) |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
多类分类器的混淆矩阵类似于二元分类器的混淆矩阵，只不过它显示了每种 预测 类别 (ŷ) 和 实际 类标签 (y) 的组合的预测次数。
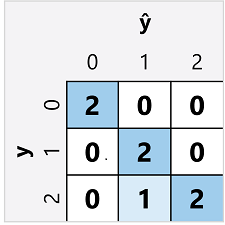
在此混淆矩阵中，我们可以按如下所示确定每个类的指标：
| 班级 | 卫生纸 | TN | FP | FN | 准确性 | 召回率 | 精准率 | F1 分数 |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 4 | 1 | 0 | 0.86 | 1.0 | 0.67 | 0.8 |
| 2 | 2 | 4 | 0 | 1 | 0.86 | 0.67 | 1.0 | 0.8 |
若要计算总体准确性、召回率和精度指标，请使用 TP、 TN、 FP 和 FN 指标总数：
- 总体准确性 = （13+6）÷（13+6+1+1） = 0.90
- 总体召回 率 = 6÷（6+1） = 0.86
- 总精度 = 6÷（6+1） = 0.86
整体 F1 分数是使用整体召回率和精准率指标计算的：
- 总 F1 分数 = （2x0.86x0.86）÷（0.86+0.86） = 0.86