矩阵转换负责很多 3D 图形的基础数学运算。
几何流水线采用顶点作为输入。 转换引擎将世界、视图和投影转换应用于顶点,剪辑结果,并将所有内容传递给光栅器。
| 转换和空间 | DESCRIPTION |
|---|---|
| 模型空间中的模型坐标 | 在管道最前端,模型的顶点是相对于本地坐标系定义的。 这是一个本地起点和方向。 坐标方向通常称为 模型空间。 单个 坐标称为模型坐标。 |
| 世界转型为世界空间 | 几何图形管道的第一个阶段将模型的顶点从其本地坐标系转换为场景中所有对象使用的坐标系。 重新定向顶点的过程称为 世界变换,它将模型空间转换为称为 世界空间的新方向。 世界空间中的每个顶点都使用 世界坐标声明。 |
| 将视图转换为视图空间(相机空间) | 在下一阶段,描述 3D 世界的顶点将相对于相机进行定向。 也就是说,你的应用程序为场景选择一个视点,世界空间坐标将重新定位并旋转在相机的视线周围,将世界空间变成 视区 (也称为 相机空间)。 这是 视图转换,它将世界空间转换为视图空间。 |
| 投影转换为投影空间 | 下一阶段是 投影转换,该阶段将视图空间转换为投影空间。 在管道的这一部分,对象通常根据与观者的距离进行缩放,从而为场景提供深度的错觉;近处的对象显示得比远处的对象更大。 为了简便起见,本文档将投影转换后顶点存在的空间称为 投影空间。 一些图形书籍可能将投影空间称为 后同质空间。 并非所有投影转换都会缩放场景中对象的大小。 此类投影有时称为 仿射 或 正交投影。 |
| 在屏幕空间中剪辑 | 在管道的最后一部分,任何在屏幕上不可见的顶点都会被移除,以避免光栅器花时间计算这些永远不会被看到的内容的颜色和阴影。 此过程称为 截取。 剪裁后,其余顶点会根据视区参数进行缩放,并转换为屏幕坐标。 当场景光栅化时,屏幕上显示的生成的顶点存在于 屏幕空间中。 |
转换用于将对象几何图形从一个坐标空间转换为另一个坐标空间。 Direct3D 使用矩阵执行 3D 转换。 矩阵创建三维转换。 可以组合矩阵以生成包含多个转换的单个矩阵。
可以在模型空间、世界空间和视图空间之间转换坐标。
矩阵转换
在处理 3D 图形的应用程序中,可以使用几何转换执行以下作:
- 表示对象相对于另一个对象的位置。
- 旋转和调整对象的大小。
- 更改查看位置、方向和视角。
可以使用 4x4 矩阵将任意点(x,y,z)转换为另一个点(x',y',z'),如以下公式所示。
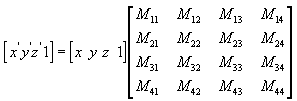
对 (x, y, z) 和矩阵执行以下公式以生成点 (x', y', z')。
新点 equations for the new point的公式
equations for the new point的公式
最常见的转换是转换、旋转和缩放。 可以将产生这些效果的矩阵合并到单个矩阵中,以一次计算多个转换。 例如,可以生成一个矩阵来转换和旋转一系列点。
矩阵按行列顺序编写。 沿每个轴均匀缩放顶点(称为统一缩放)的矩阵使用数学表示法表示以下矩阵。
用于统一缩放 矩阵的
在C++中,Direct3D 使用矩阵结构将矩阵声明为二维数组。 以下示例演示如何初始化 D3DMATRIX 结构以充当统一缩放矩阵(比例因子“s”)。
D3DMATRIX scale = {
5.0f, 0.0f, 0.0f, 0.0f,
0.0f, 5.0f, 0.0f, 0.0f,
0.0f, 0.0f, 5.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f
};
翻译
以下公式将点 (x, y, z) 转换为新点 (x', y', z')。
对新点 的平移矩阵的方程是
可以在C++中手动创建翻译矩阵。 以下示例显示了创建矩阵以转换顶点的函数的源代码。
D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
D3DXMATRIX ret;
D3DXMatrixIdentity(&ret);
ret(3, 0) = dx;
ret(3, 1) = dy;
ret(3, 2) = dz;
return ret;
} // End of Translate
缩放
以下公式按 x-、y-和 z 方向中的任意值将点(x、y、z)缩放为新点(x'、y'、z')。
新点 的刻度矩阵
旋转
此处所述的转换适用于左手坐标系,因此可能与你在其他地方看到的转换矩阵不同。
以下公式围绕 x 轴旋转点 (x, y, z),生成新点 (x', y', z')。
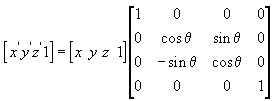 的 x 轴旋转矩阵的公式
的 x 轴旋转矩阵的公式
以下公式使点围绕 y 轴旋转。
 的 y 旋转矩阵公式
的 y 旋转矩阵公式
以下公式使点绕 z 轴旋转。
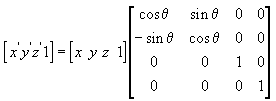 的 z 旋转矩阵公式
的 z 旋转矩阵公式
在这些示例矩阵中,希腊文字母 theta 代表旋转角度(以弧度为单位)。 沿旋转轴向原点观察时,按顺时针方式测量角度。
以下代码显示了一个函数,用于处理有关 X 轴的旋转。
// Inputs are a pointer to a matrix (pOut) and an angle in radians.
float sin, cos;
sincosf(angle, &sin, &cos); // Determine sin and cos of angle
pOut->_11 = 1.0f; pOut->_12 = 0.0f; pOut->_13 = 0.0f; pOut->_14 = 0.0f;
pOut->_21 = 0.0f; pOut->_22 = cos; pOut->_23 = sin; pOut->_24 = 0.0f;
pOut->_31 = 0.0f; pOut->_32 = -sin; pOut->_33 = cos; pOut->_34 = 0.0f;
pOut->_41 = 0.0f; pOut->_42 = 0.0f; pOut->_43 = 0.0f; pOut->_44 = 1.0f;
return pOut;
}
串联矩阵
使用矩阵的一个优点是,可以通过乘以矩阵来组合两个或多个矩阵的效果。 这意味着,若要旋转模型,然后将其转换为某个位置,无需应用两个矩阵。 相反,将旋转和翻译矩阵相乘以生成包含其所有效果的复合矩阵。 此过程称为矩阵串联,可以使用以下公式编写。
矩阵串联公式 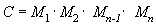
在此公式中,C 是正在创建的复合矩阵,而 M₁ 到 Mₙ 是单个矩阵。 在大多数情况下,只有两个或三个矩阵是串联的,但没有限制。
执行矩阵乘法的顺序至关重要。 前面的公式反映了矩阵串联的从左到右规则。 也就是说,用于创建复合矩阵的矩阵的可见效果按从左到右的顺序发生。 以下示例显示了典型的世界矩阵。 想象一下,你正在为一个典型的飞碟构建世界坐标矩阵。 你可能想要让飞碟围绕其中心——模型空间的y轴——旋转,并将其移动到场景中的其他位置。 若要实现此效果,首先创建一个旋转矩阵,然后将其乘以转换矩阵,如以下公式所示。
基于旋转矩阵和平移矩阵的旋转公式 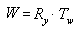
在此公式中,Ry 是一个矩阵,用于旋转 y 轴,Tw 是世界坐标中某些位置的转换。
乘矩阵的顺序很重要,因为与乘以两个标量值不同,矩阵乘法不是可交换的。 按照相反的顺序相乘矩阵,视觉上就可以先将飞碟移动到其在世界空间中的位置,然后围绕世界坐标原点旋转。
无论你创建的矩阵类型如何,请记住从左到右的规则,以确保达到预期的效果。
相关主题