m×n 矩阵是一组以 m 行排列的数字,n 个 列。 下图显示了多个矩阵。
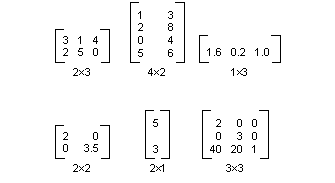
可以通过添加单个元素来添加大小相同的两个矩阵。 下图显示了矩阵加法的两个示例。
显示如何执行矩阵添加插图
m×n 矩阵可以乘以 n×p 矩阵,结果是 m×p 矩阵。 第一个矩阵中的列数必须与第二个矩阵中的行数相同。 例如,4 ×2 矩阵可以乘以 2 ×3 矩阵来生成 4 ×3 矩阵。
可以将矩阵的平面和行和列中的点视为向量。 例如,(2,5)是具有两个组件的向量,(3、7、1)是具有三个组件的向量。 两个向量的点积定义如下:
(a, b) • (c, d) = ac + bd
(a, b, c) • (d, e, f) = ad + be + cf
例如,(2,3)和(5,4)的点积为 (2)(5) + (3)(4) = 22。 (2, 5, 1) 和 (4, 3, 1) 的点积是 (2)(4) + (5)(3) + (1)(1) = 24。 请注意,两个向量的点积是一个数字,而不是另一个向量。 另请注意,仅当两个向量具有相同数量的组件时,才能计算点积。
让 A(i, j) 成为第 行的矩阵 A 中的条目,第列的第 j 列。 例如,A(3,2)是 3rd 行和第 2 列中矩阵 A 中的条目。 假设 A、B 和 C 是矩阵,AB = C。C 条目的计算方式如下:
C(i, j) = (A 行 i) • (B 列 j)
下图显示了矩阵乘法的几个示例。
显示如何执行矩阵乘法插图
如果将平面中的某个点视为 1 × 2 矩阵,则可以通过将点乘以 2 × 2 矩阵来转换该点。 下图显示了应用于点(2,1)的多个转换。
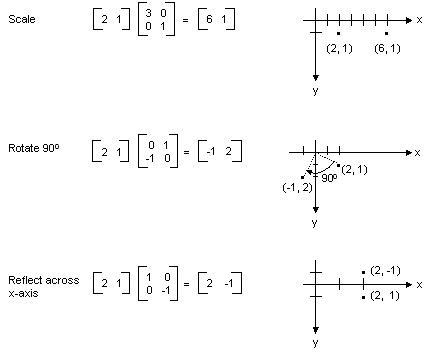
上图中显示的所有转换都是线性转换。 某些其他转换(如转换)不是线性的,不能用 2 × 2 矩阵表示乘法。 假设你想要从点(2,1)开始旋转它 90 度,在 x 方向翻译 3 个单位,并在 y 方向转换 4 个单位。 可以通过执行矩阵乘法,然后添加矩阵来实现此目的。
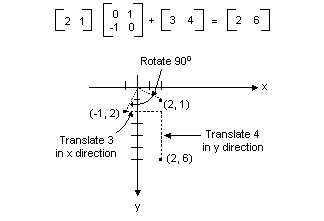
线性转换(乘以 2 × 2 矩阵的乘法),后跟一个转换(添加 1 × 2 矩阵)称为仿生转换。 将相交转换存储在一对矩阵(一个用于线性部分和一个用于转换)中的替代方法是将整个转换存储在 3 × 3 矩阵中。 若要执行此作,平面中的点必须存储在一个具有虚拟第三坐标的 1 × 3 矩阵中。 通常的技术是使所有第三个坐标都等于 1。 例如,点(2,1)由矩阵 [2 1 1] 表示。 下图显示了一个相交转换(旋转 90 度;在 x 方向转换 3 个单位,y 方向为 4 个单位),表示为乘法的单个 3 × 3 矩阵。
显示矩阵乘法如何执行相亲转换图示
在前面的示例中,点(2,1)映射到点(2,6)。 请注意,3 × 3 矩阵的第三列包含数字 0、0、1。 对于相交转换的 3 × 3 矩阵,这始终是这种情况。 重要数字是列 1 和 2 中的六个数字。 矩阵的左上角 2 × 2 部分表示转换的线性部分,第三行的前两个条目表示转换。
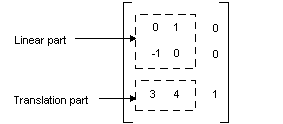
在 Windows GDI+ 中,可以在 Matrix 对象中存储相交转换。 由于表示相交转换的矩阵的第三列始终为 (0, 0, 1),因此在构造 Matrix 对象时,仅指定前两列中的六个数字。 该语句 Matrix myMatrix(0.0f, 1.0f, -1.0f, 0.0f, 3.0f, 4.0f); 构造上图中显示的矩阵。
复合转换
复合转换是一系列转换,后跟另一个转换。 请考虑以下列表中的矩阵和转换:
- 矩阵 A 旋转 90 度
- 矩阵 B 按 x 方向的 2 系数缩放
- 矩阵 C 在 y 方向转换 3 个单位
如果从点(2,1)开始(由矩阵 [2 1 1] 表示),然后乘以 A,然后 B,然后 C,该点(2,1)将按列出的顺序进行三个转换。
[2 1 1]ABC = [ –2 5 1]
无需将复合转换的三个部分存储在三个单独的矩阵中,可以将 A、B 和 C 相乘,以获取存储整个复合转换的单个 3 × 3 矩阵。 假设 ABC = D。然后,乘以 D 的点将得到与 A 乘以 A、B、C 相同的结果。
[2 1 1]D = [ –2 5 1]
下图显示了矩阵 A、B、C 和 D。
显示如何通过将构成矩阵乘以图示
复合转换的矩阵可以通过乘以单个转换矩阵来形成的事实意味着任何相交转换序列都可以存储在单个 矩阵 对象中。
注意
复合转换的顺序非常重要。 一般情况下,旋转,然后缩放,然后翻译与刻度不同,然后旋转,然后翻译。 同样,矩阵乘法的顺序也很重要。 通常,ABC 与 BAC 不同。
Matrix 类提供了几种方法用于生成复合转换:Matrix::Multiply、Matrix::Rotate、Matrix::RotateAt、Matrix::Scale、Matrix::Shear和 Matrix::Translate。 以下示例创建复合转换的矩阵,该矩阵首先旋转 30 度,然后按 y 方向的 2 系数缩放,然后在 x 方向转换 5 个单位。
Matrix myMatrix;
myMatrix.Rotate(30.0f);
myMatrix.Scale(1.0f, 2.0f, MatrixOrderAppend);
myMatrix.Translate(5.0f, 0.0f, MatrixOrderAppend);
下图显示了矩阵。
