Grover 搜尋演算法的理論
在本文中,您將找到一個詳細的理論說明,說明讓 Grover 演演算法運作的數學原則。
如需 Grover 演演算法的實際實作來解決數學問題,請參閱 實作 Grover 的搜尋演算法。
問題的陳述
任何搜尋工作都可以使用接受搜尋專案 $x$ 的抽象函式 $f(x)$ 來表示。 如果專案 $x$ 是搜尋工作的方案,則 $f(x)=1$。 如果專案 $x$ 不是方案,則 $f(x)=0$。 搜尋 問題 包含尋找任何專案 $x_0$ , $例如 f(x_0)=1$。
Grover 演算法的目標工作可以如下表示:假設有一個傳統函$式 f(x):\{0,1\}^n \rightarrow\{0,1\}$,其中 $n$ 是搜尋空間的位大小,請尋找 f(x_0)=1$ 的$輸入$x_0$。 演算法的複雜度是由函式 f(x)$ 的使用$次數來測量。 在最壞的情況下, $f(x)$ 必須總共 $評估 N-1$ 次,其中 $N=2^n$,嘗試所有可能性。 N-1$ 元素之後$,它必須是最後一個專案。 Grover 的量子演算法可以更快解決這個問題,提供二次加速。 此處的二次方表示,相較於 $N$,只需要大約 $\sqrt{N}$ 個評估。
演算法的大綱
假設搜尋工作有 $N=2^n$ 個符合資格的專案,而且會藉由將每個專案指派一個從 $0$ 到 $N-1$ 的整數來編製索引。 此外,假設有 $M$ 不同的有效輸入,表示有$$M 輸入,f$(x)=1$。 然後演算法的步驟如下:
- 從狀態初始化$\ket{0}$的 $n$ 量子位緩存器開始。
- 將 H 套用$至緩存器的每個量子位,將緩存器準備成統一迭加:$$|\text{緩存}\rangle=\frac{1}{\sqrt{器 N\sum}}_{x=0}^{N-1}|x$\rangle$$
- 將下列作業套用至快取器 $N_{\text{最佳}}$ 時間:
- 階段 oracle $O_f$ ,針對解決方案專案套用條件式階段移 $位 -1$ 。
- 將 H$ 套$用至緩存器中的每個量子位。
- 除了 以外的$\ket{0}$每個計算基礎狀態,條件式階段移位為 $-1$。 這可由單一運算 $-O_0$來表示,因為 $O_0$ 只表示條件式階段移位 $\ket{0}$ 。
- 將 H$ 套$用至緩存器中的每個量子位。
- 測量快取器,以取得具有非常高機率之方案之專案的索引。
- 檢查其是否為有效的解決方案。 如果沒有,請重新開始。
$\text{N_optimal=\left}\lfloor \pi{4}\sqrt{\frac{}{N}{M}}-{2}\right\frac{1}{\rfloor \frac{$ 是最佳反覆項目數目,可藉由測量緩存器來最大化取得正確專案的可能性。
注意
步驟3.b、3.c和3.d的聯合應用在文學中通常被稱為格羅弗的擴散運算符。
套用至緩存器的整體一元運算為:
$$(-H^ n}O_0H{\otimes^{\otimes n O_f})^{N_{\text{最佳}}}H^{\otimes n}$$
依照註冊的狀態逐步執行
為了說明此程式,讓我們遵循緩存器狀態的數學轉換,簡單案例中只有兩個量子位,而有效元素為 $\ket{01}。$
緩存器會以狀態啟動: $$|\text{register}\rangle=|00\rangle$$
將 $H 套用至每個量子位之後,緩存器的狀態會轉換成:$$|\text{register\sum{1}{\sqrt{}\rangle{4}}=\frac{_{i \in \{0,1\}^2 i\rangle=\frac12}|(\ket{00}++\ket{01}+)\ket{10}\ket{11}$$$
然後,階段 Oracle 會套用至 get:$$|\text{register}\rangle=\frac12({00}\ket{-{01}\ket{++)\ket{\ket{{10}{11}$$
然後 $H$ 會再次對每個量子位執行動作,以提供:$$|\text{緩存=\frac}\rangle器 12(\ket{{00}+\ket{{01}-\ket{{10}+)\ket{{11}$$
現在,條件式階段移會套用至每個狀態,但 :$\ket{00}$$$|\text{register}\rangle\frac=12({00}\ket{--\ket{{01}+\ket{{10}-)\ket{{11}$$
最後,第一個 Grover 反覆專案會再次套用 $H$ 以取得: $$|\text{register}\rangle=\ket{{01}$$
遵循上述步驟,即可在單一反覆專案中找到有效的專案。 如您稍後所見,這是因為 N=4 和單一有效專案 $N_\text{最佳}=1$。
幾何說明
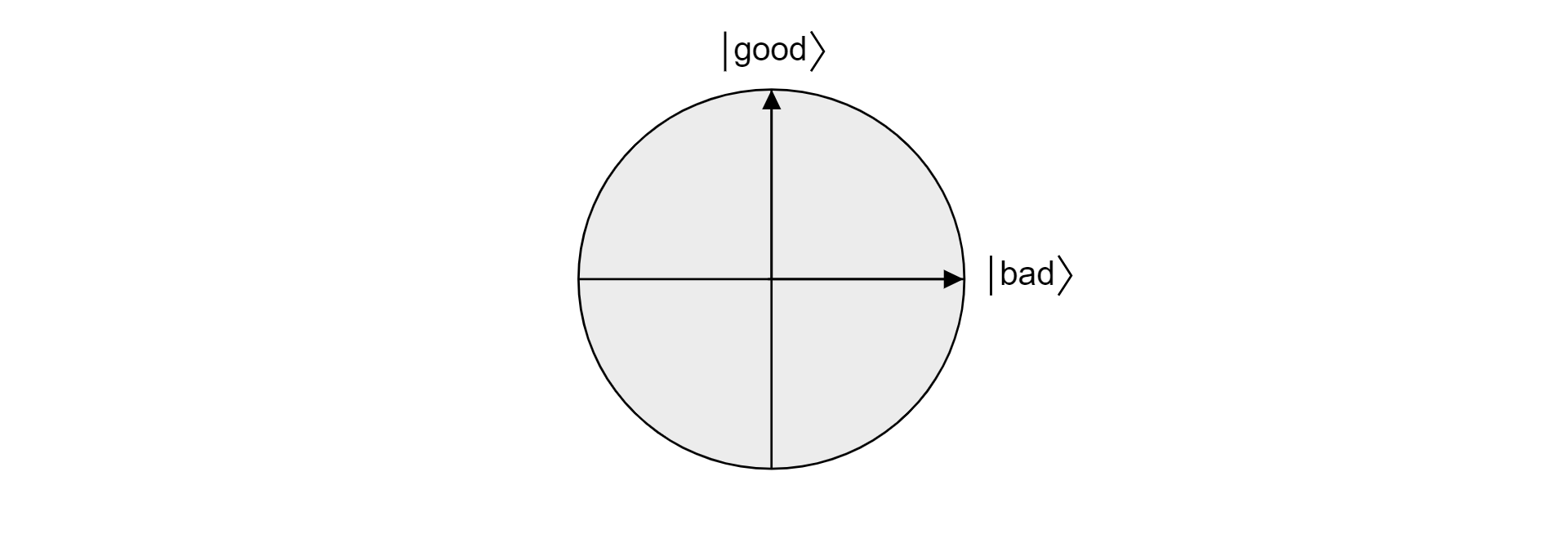
若要查看 Grover 演演算法的運作原因,讓我們從幾何角度來研究演算法。 讓 $\ket{\text{「壞}}$ 」成為不是搜尋問題解決方案之所有狀態的迭加。 Supposing 有 $M$ 有效的解決方案:
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
狀態 $\ket{\text{良好}}$ 定義為所有狀態的迭加, 這些狀態是 搜尋問題的解決方案:
$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
由於好壞是互斥集合,因為專案無效且無效,所以好壞$\ket{\text{}}$的狀態$\ket{\text{}}$是正交的。 這兩種狀態都會形成向量空間中平面的正交基礎。 人們可以使用這個平面來可視化演算法。
現在,假設$\ket{\psi}$是一種任意狀態,存在於飛機上,跨越$\ket{\text{好}}$壞$\ket{\text{}}$。 生活在該平面中的任何狀態都可以以下列形式表示:
$$\ket{\psi}=\alpha\ket{\text{良好}} + \beta\ket{\text{壞}}$$
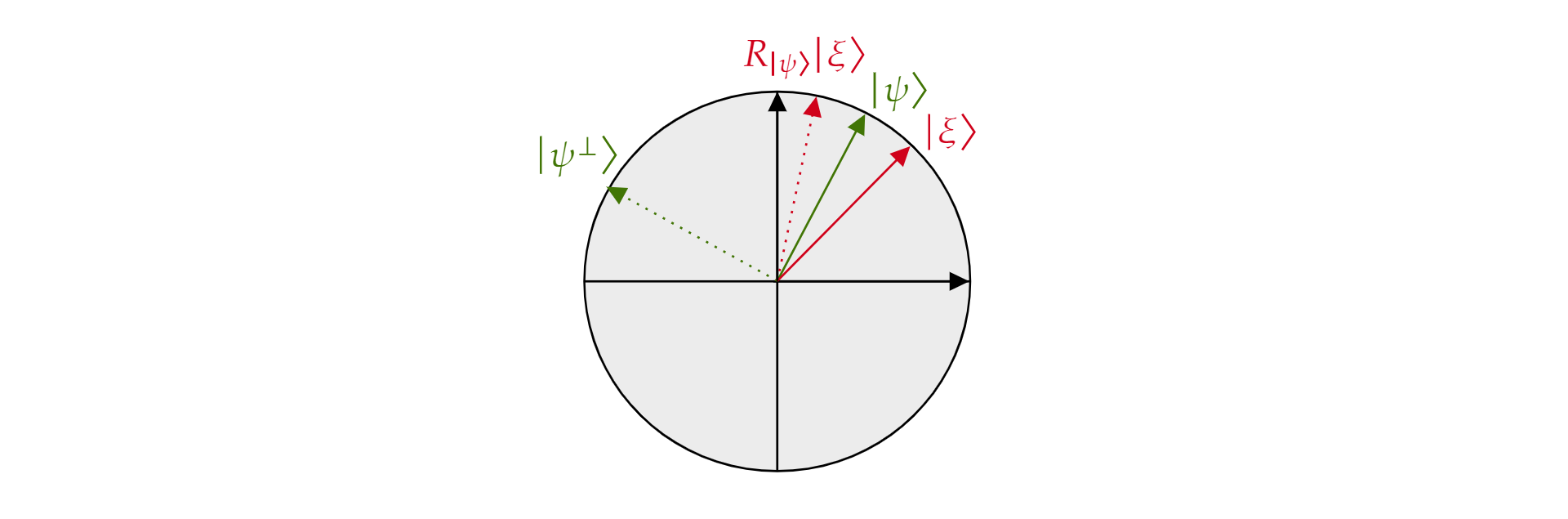
其中 $\alpha$ 和 $\beta$ 是實數。 現在,讓我們介紹反映運算符 $R_{\ket{\psi}}$,其中 $\ket{\psi}$ 是位於平面中的任何量子位狀態。 運算子定義為:
$${\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$
它稱為反映運算符, $\ket{\psi}$ 因為它可以幾何方式解譯為有關 方向的 $\ket{\psi}$反映。 若要查看它,請採用 所 $\ket{\psi}$ 形成平面的正交基礎及其正交補 $\ket{\psi碼 ^{\perp}}$。 平面的任何狀態 $\ket{\習}$ 都可以以這類基礎分解:
$$\ket{\習}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
如果運算子R_{\ket{\psi}}$套用$至 $\ket{\習}$:
$${\ket{\psi}}\ket{R_\習}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
運算子 $R_\ket{\psi}$ 反轉元件正交, $\ket{\psi}$ 但讓 $\ket{\psi}$ 元件保持不變。 因此, $R_\ket{\psi}$ 是 關於的 $\ket{\psi}$反映。
Grover 的演算法,在每個量子位的第一個應用$$之後,會以所有狀態的統一迭加開始。 這可以撰寫為:
$$\ket{\text{all}}\sqrt{\frac{=M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
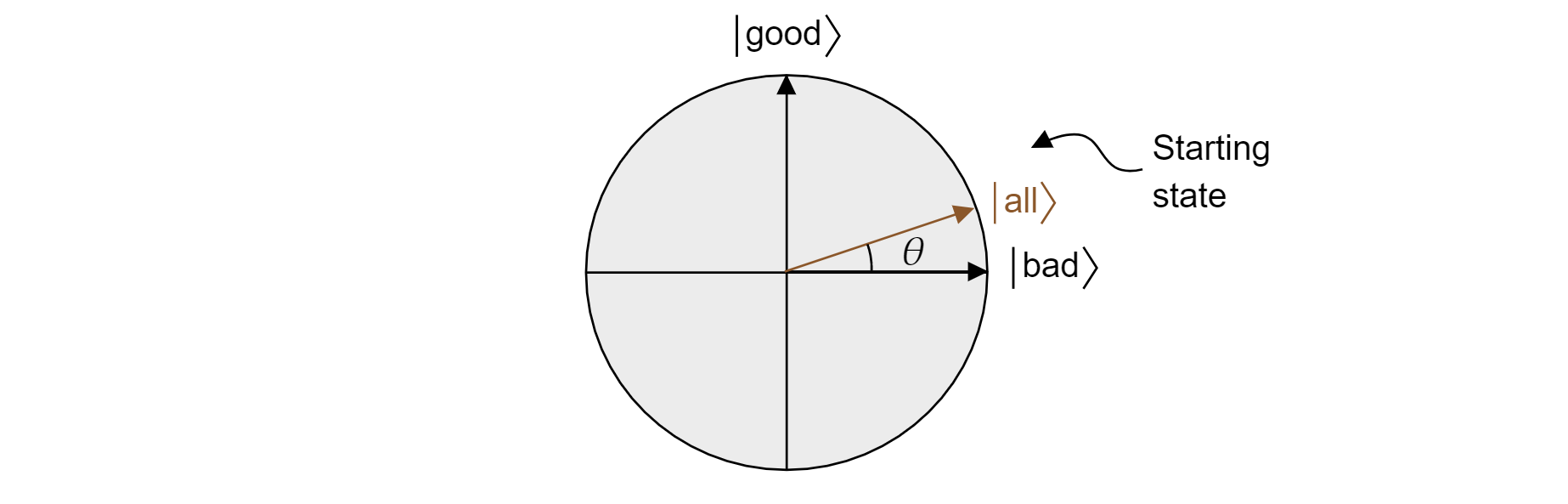
因此,國家住在飛機上。 請注意,從相等迭加測量時取得正確結果的機率只是 $|\braket{\text{好}|{\text{全部}}}|^2=M/N$,這是您從隨機猜測中預期的結果。
oracle $O_f$ 會將負階段新增至搜尋問題的任何解決方案。 因此,它可以寫入為不良}}$座標軸的$\ket{\text{反映:
$$={\ket{\text{O_f R_bad=}}} 2\ket{\text{壞}}\bra{\text{}} - \mathcal{I}$$
同樣地,條件式階段轉移 $O_0$ 只是狀態 $\ket{0}$的反轉反映:
$$O_0 = R_ -2\ket{{0}\bra{0} + \mathcal{{\ket{0}}= I}$$
知道這個事實,很容易檢查 Grover 擴散作業 $-H^{\otimes n} O_0 H^{\otimes n}$ 也是所有}$狀態$\ket{的反映。 只要執行:
$$-H^ n} O_0 H^ n}=2H{\otimes^{\otimes{\otimes n H{\otimes^ n}}\ket{0}\bra{{0} -H^{\otimes n}\mathcal I}H^{\otimes n=} 2\ket{\text{all}}\bra{\text{}} - \mathcal{{I}= R_all{\ket{\text{}}}$$
已示範 Grover 演算法的每個反覆專案都是兩個反映 $的組成,\ket{\text{R_bad}}$ 和 $R_\ket{\text{all}}$。
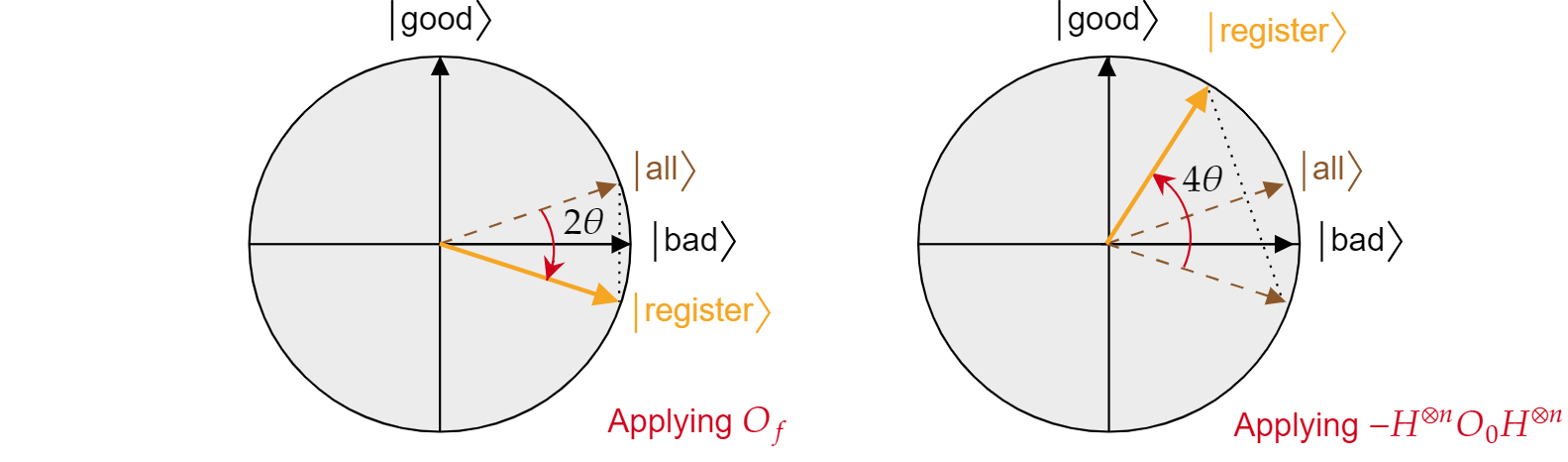
每個 Grover 反覆項目的組合效果是角度 $2\theta$ 的逆時針旋轉。 幸運的是,\theta$ 的角度$很容易找到。 因為 $\theta$ 只是所有}}$與$\ket{\text{壞}}$之間的$\ket{\text{角度,因此可以使用純量產品來尋找角度。 已知 $\cos{\theta}=\braket{\text{全都}|\text{不好}}$,所以一個人需要計算 $\braket{\text{所有}|\text{壞的}}$。 從壞和好方面分解$\ket{\text{一切$\ket{\text{}}$,它遵循:}}$$\ket{\text{}}$
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
緩存器狀態與 $\ket{\text{良好}}$ 狀態之間的角度會隨著每個反覆項目而減少,因而產生較高的測量有效結果機率。 若要計算此機率,您只需要計算$|\braket{\text{良好的快取器}}|^2$}|\text{。 表示 good}}$ 和 $\ket{\text{register$\gamma}}$ (k)$之間的$\ket{\text{角度,其中 $k$ 是反覆項目計數:
$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
因此,成功的機率是:
$$P(\text{success}) = \cos^2(\gammak)) = \sin^2\left[(2k +1)\arccos \left(\sqrt{\frac{N-M}{N}}\right)]\right$$
最佳反覆項目數目
由於成功機率可以寫入為反覆項目數目的函式,因此可以藉由計算最小正整數來找出最佳反覆運算數N_{\text{}}$最佳反覆運算數$,而此整數會最大化成功機率函式。
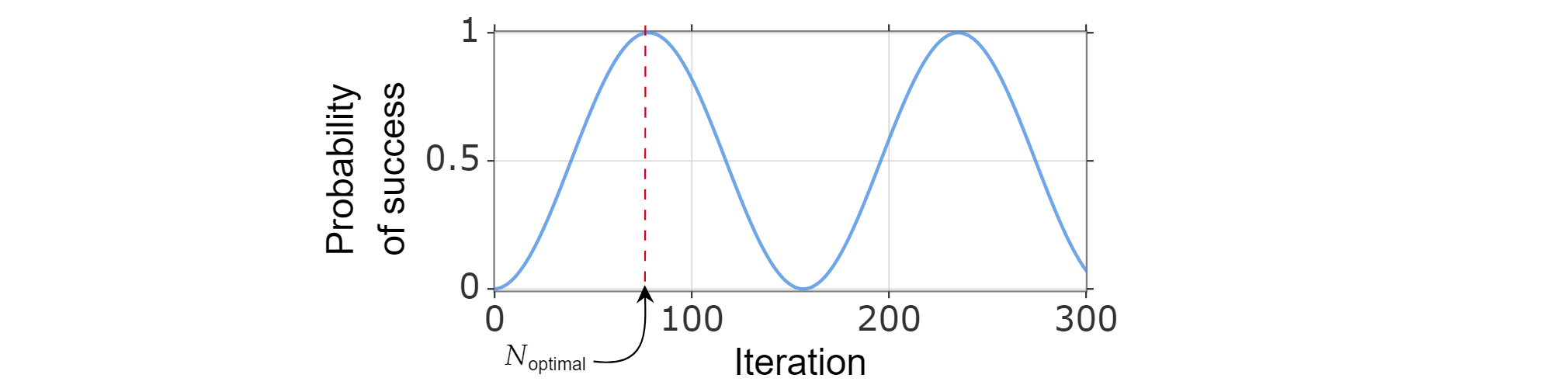
已知 $\sin^2{x}$ 達到 x=\frac{\pi}{2}$ 的第一個最大值$,因此:
$$\frac{\pi}{{2}=(2k_{\text{佳}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
這會提供:
$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2\frac{= \pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N)}\right$$
在最後一個步驟中,$\arccos \sqrt{1-x\sqrt{=}+} O(x^{3/2})的位置。$
因此,您可以挑選$N_\text{\text{最佳}$$N_optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{2}\right\rfloor。$
複雜度分析
從先前的分析中,$需要 Oracle $O_f$的 O\left(\sqrt{\frac{N}{M}}\right)$ 查詢,才能尋找有效的專案。 不過,演算法是否可以在時間複雜度方面有效率地實作? $$O_0是以 n$ 位計算$布爾運算為基礎,已知可使用 O(n)$ 閘道實作$。 還有兩層 $n$ 哈達馬德門。 因此,這兩個元件只需要 $每個反覆專案的 O(n)$ 網關。 因為 $N=2^n$,所以遵循 $O(n)=O(log(N))。$ 因此,如果需要$每次反覆運算的 O(N}{M}}\right)$ 反覆運算和 $O\left(\sqrt{\frac{log(N)閘道$,則總時間複雜度(而不考慮 Oracle 實作)是 $O\left(N M}}記錄(\sqrt{\frac{N}{)\right$。
演演算法的整體複雜度最終取決於 oracle $O_f$ 實作的複雜性。 如果量子計算機上的函式評估比傳統計算機複雜得多,則整體演算法運行時間在量子案例中會更長,即使從技術上而言,它仍會使用較少的查詢。
參考資料
如果您想要繼續瞭解 Grover 的演算法,您可以檢查下列任何來源:
- 洛夫·格羅弗的原創論文
- 尼爾森的量子搜尋演算法區段,M. A. &放大器;莊, I. L. (2010 年) 。 量子計算和量子資訊。
- Grover 在 Arxiv.org 上的演算法