本文說明 T 閘道和 T Factory 在容錯量子運算中的角色。 提供量子演算法時,執行 T 閘道和 T Factory 所需的資源估計對於判斷演算法的可行性至關重要。 Azure Quantum 資源估算器會計算執行演算法所需的 T 狀態數目、單一 T 處理站的實體量子位數目,以及 T Factory 的運行時間。
一組通用量子閘道
根據 DiVincenzo 的標準, 可調整的量子計算機必須能夠實作一 組通用量子閘道。 通用集合包含執行任何量子計算所需的所有閘道,也就是說,任何計算都必須分解回有限序列的通用閘道。 量子計算機至少必須能夠將單一量子位移至 Bloch Sphere 上的任何位置(使用單一量子位網關),並在系統中引入糾纏,這需要多量子位網關。
在經典電腦上,只有四個函數能將一個位元映射到另一個位元。 相反地,量子計算機上的單一量子位上會有無限數量的單一轉換。 因此,沒有一組有限的基本量子作業或閘道,可以完全復寫量子運算中允許的無限一組單一轉換。 這表示,與傳統運算不同,量子計算機不可能完全使用有限數目的閘道來實作每個可能的量子程式。 因此,量子計算機在傳統計算機的同一意義上不能是通用的。 因此,當我們說一組閘對量子運算而言是 通用 的時,我們實際上意味著比傳統運算更弱一些的東西。
為了獲得通用性,量子計算機只需要 使用有限長度閘道序列來近似 有限誤差內的每一個單位矩陣。
換句話說,一組閘道是一個通用閘道集,如果任何一元轉換可以大致寫成這個集合的網關乘積。 對於任何指定的錯誤界限,必須從閘門集合中有閘門$G_{1},G_{2},\ldots,G_N$
$$ {G_N G_N-1}\cdots G_2 G_1 \approx U.$$
因為矩陣乘法的慣例是從右到左乘,因此在這個序列中第一個的閘運算 $G_N$ 實際上是最後一個應用於量子狀態向量的。 更正式地說,當對於每一個誤差容忍度 $\epsilon> 有一組 $G_1, \ldots, G_N$ 存在,使得 $G_N\ldots G_1$ 和 $U$ 之間的距離最多為$\epsilon$ 時,這樣的閘門集才被稱為通用的。 在理想情況下,要達到 \epsilon 的距離所需的 N 值應該隨著 1/\epsilon 的變化而呈現多對數縮放。
例如,由 Hadamard、CNOT 和 T 閘道形成的集合是一個通用集合,從中可以產生任何量子計算(在任何數目的量子位上)。 Hadamard 和 T 閘組可以生成任何單量子比特閘:
$$H=\frac{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1\end{bmatrix},\qquad T=\begin{bmatrix} 1 & 0 \\0 & e^{i\pi/4}\end{bmatrix}. $$
在量子計算機中,量子網關可分為兩個類別:Clifford 網關和非 Clifford 網關,在此案例中為 T 閘道。 只有 Clifford 閘道產生的量子程式可以使用傳統電腦有效率地模擬,因此需要非 Clifford 閘道才能取得量子優勢。 在許多量子誤差修正(QEC)方案中,所謂的 Clifford 門很容易實作,也就是說,其操作和量子位資源需求很少,就可以以容錯方式實作,而非 Clifford 門在需要容錯時相當昂貴。 在通用量子網關集中,T 閘道通常用來作為非 Clifford 閘道。
默認情況下,包含在 Q# 的單量子位 Clifford 閘門標準集合包括
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 , \end{bmatrix} S \qquad 1 =\begin{bmatrix}amp; 0 & 0 \\amp; i & T^2,\end{bmatrix}= X\qquad 0 =\begin{bmatrix}amp;1 & 1\\amp; 0 & HT^4H,\end{bmatrix}=$$
$$Y =0 amp; -i \begin{bmatrix}& amp; 0 \\T^2HT^4 HT^6, & Z\end{bmatrix}=1\qquadamp;=\begin{bmatrix}&0 0\\& amp;-1 \end{bmatrix}=T^4。 $$
與非 Clifford 閘(T 閘)一起,這些操作可以組合起來,以近似單一量子位的任何酉變換。
Azure Quantum 資源估算器中的 T Factory
非 Clifford T 閘道準備非常重要,因為其他量子閘道不足以進行通用量子計算。 若要實作實際規模演算法的非 Clifford 作業,則需要低誤差率 T 閘(或 T 狀態)。 不過,它們可能很難直接在邏輯量子位上實作,而且對於某些實體量子位來說也可能很困難。
在容錯量子計算機中,所需的低誤差率 T 狀態是由 T 狀態蒸餾廠產生,簡稱為 T Factory。 這些 T Factory 通常牽涉到一連串的釀酒,其中每個回合都會採用以較小的距離代碼編碼的許多嘈雜 T 狀態、使用釀酒單位處理它們,並輸出較少以較大距離代碼編碼的較不嘈雜 T 狀態,而輪數、釀酒單位和距離全都是可變動的參數。 此程序會重複進行,其中一輪的輸出狀態 T 會作為輸入送入下一輪。
根據 T Factory 的持續時間, Azure Quantum 資源估算器 會決定在 T Factory 超過演算法的總運行時間之前叫用 T Factory 的頻率,以及演算法運行時間期間可產生多少 T 狀態。 通常,在演算法運行期間,所需的 T 狀態數量超過單一 T 工廠調用可以產生的數量。 為了產生更多 T 狀態,資源估算器會使用 T Factory 的複本。
T Factory 實體預估
資源估算器會計算執行演算法所需的 T 狀態總數,以及單一 T Factory 及其運行時間的實體量子位數目。
目標是在演算法運行時間內產生所有 T 狀態,盡可能少一些 T Factory 複本。 下圖顯示演算法的運行時間和一個 T Factory 的運行時間範例。 您可以看到 T Factory 的執行時間比演算法的執行時間短。 在此範例中,一個 T Factory 可以擷取一個 T 狀態。 出現了兩個問題:
- 在演算法結束之前,T factory 可以被呼叫多少次?
- 在演算法運行時間期間,需要多少個 T 工廠蒸餾回合復本,才能建立所需的 T 狀態數目?
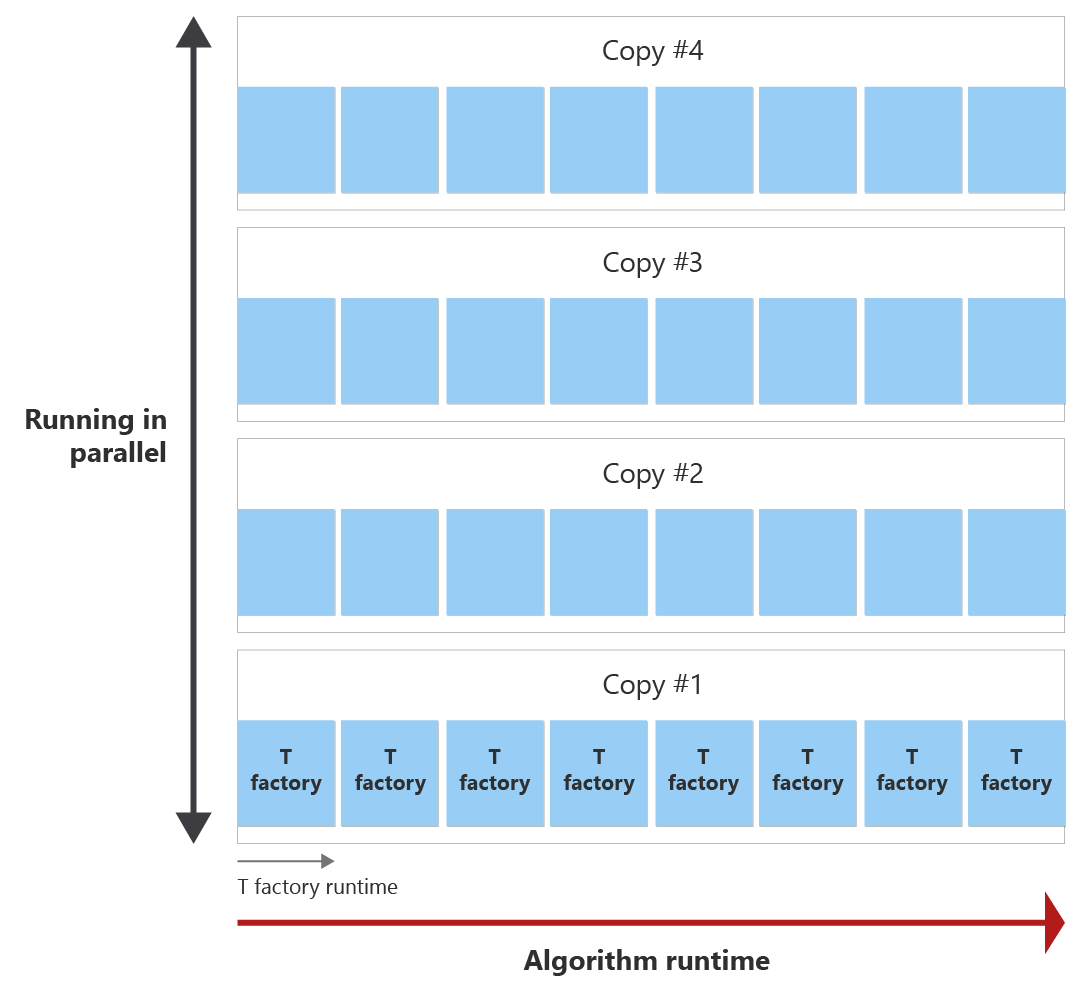
在演算法結束之前,可以叫用 T Factory 八次,這稱為釀酒回合。 例如,如果您需要 30 個 T 狀態,則會在演算法運行時間期間叫用單一 T Factory 八次,因此它會建立八個 T 狀態。 然後,您需要四個平行運行的 T 工廠蒸餾輪,以提取所需的 30 個 T 狀態。
注意
請注意,T Factory 複本與 T Factory 調用並不相同。
T 狀態蒸餾工廠是以一連串的回合實現,每個回合都包含一組平行運行的蒸餾單位複製品。 資源估算器會計算執行一個 T Factory 所需的實體量子位數目,以及 T Factory 執行多久,以及其他必要參數。
您只能執行 T 處理站的完整呼叫。 因此,在某些情況下,所有 T Factory 調用的累積運行時間小於演算法運行時間。 由於量子位在不同的循環中重複使用,因此一個 T 工廠所需的實體量子位數目是單次循環中使用的實體量子位數目的上限。 T Factory 的執行時間是所有回合中的執行時間總和。
注意
如果實體 T 閘道錯誤率低於所需的邏輯 T 狀態錯誤率,則資源估算器無法執行良好的資源估計。 當您提交資源估算作業時,可能會發現無法找到 T 工廠,因為所需的邏輯 T 狀態錯誤率可能過低或過高。
如需詳細資訊,請參閱評估需求以調整為實際量子優勢的附錄 C。