Přehled metod prognózování v AutoML

  • Článek

Tento článek se zaměřuje na metody, které AutoML používá k přípravě dat časových řad a vytváření modelů prognóz. Pokyny a příklady pro trénování modelů prognóz v Automatizovaném strojovém učení najdete v našem článku o nastavení automatizovaného strojového učení pro prognózování časových řad .

AutoML používá k předpovídání hodnot časových řad několik metod. Tyto metody lze zhruba přiřadit do dvou kategorií:

  1. Modely časových řad, které používají historické hodnoty cílového množství k předpovědím do budoucnosti.
  2. Regrese neboli vysvětlující modely, které používají vysvětlující proměnné k předpovídání hodnot cíle.

Představte si například problém prognózy denní poptávky po konkrétní značce pomerančového džusu z obchodu s potravinami. Nechte $y_t$ reprezentovat poptávku po této značce v den $t$. Model časové řady predikuje poptávku na $t+1$ s využitím některé funkce historické poptávky.

$y_{t+1} = f(y_t, y_{t-1}, \ldots, y_{t-s})$.

Funkce $f$ má často parametry, které ladíme pomocí pozorované poptávky z minulosti. Množství historie, kterou $f$ používá k vytváření předpovědí, $s$, lze také považovat za parametr modelu.

Model časové řady v příkladu poptávky po pomerančovém džusu nemusí být dostatečně přesný, protože používá pouze informace o minulé poptávce. Existuje mnoho dalších faktorů, které pravděpodobně ovlivňují budoucí poptávku, například cena, den v týdnu a to, jestli se jedná o svátek nebo ne. Představte si regresní model , který používá tyto vysvětlující proměnné.

$y = g(\text{price}, \text{den v týdnu}, \text{svátek})$.

Opět platí, že $g$ má obecně sadu parametrů, včetně těch, které řídí regularizaci, které AutoML ladí pomocí minulých hodnot poptávky a prediktorů. Z výrazu vynecháme $t$, abychom zdůraznili, že regresní model k předpovědím používá korelační vzory mezi současně definovanými proměnnými. To znamená, že abychom mohli předpovědět $y_{t+1}$ od $g$, musíme vědět, na který den v týdnu spadá $t+1$ a jestli se jedná o svátek, a cenu pomerančového džusu v den $t+1$. První dvě informace jsou vždy snadno nalezeny na základě kalendáře. Maloobchodní cena je obvykle stanovena předem, takže cena pomerančového džusu je pravděpodobně známa i jeden den dopředu. Cena však nemusí být do 10 dnů do budoucnosti známa! Je důležité si uvědomit, že užitečnost této regrese je omezená tím, jak daleko do budoucnosti potřebujeme prognózy, označované také jako horizont prognózy, a do jaké míry známe budoucí hodnoty vysvětlujících proměnných.

Důležité

Modely prognózovací regrese automatizovaného strojového učení předpokládají, že všechny funkce poskytované uživatelem budou známy v budoucnu, alespoň do horizontu prognózy.

Regresní modely autoML je také možné rozšířit tak, aby používaly historické hodnoty cíle a vysvětlujících proměnných. Výsledkem je hybridní model s charakteristikami modelu časové řady a čistě regresní model. Historická množství jsou další vysvětlující proměnné v regresi a označujeme je jako zpožděné množství. Pořadí prodlevy odkazuje na to, jak daleko od této hodnoty je známá. Například aktuální hodnota zpoždění objednávky a 2 v cíli pro náš příklad poptávky po pomerančovém džusu je pozorovaná poptávka po šťávě z doby před dvěma dny.

Dalším rozdílem mezi modely časových řad a regresní modely je způsob, jakým generují prognózy. Modely časových řad jsou obecně definovány rekurzemi a vytvářejí prognózy jednotlivě. Pokud chtějí předpovídat mnoho období do budoucnosti, iterují se nahoru k horizontu prognózy a předchozí prognózy se vrátí zpět do modelu, aby se podle potřeby vygenerovala další prognóza s předstihem o jedno období. Naproti tomu regresní modely jsou tzv. přímé prognostiky , které generují všechny prognózy až do horizontu najednou. Přímé prognostiky mohou být vhodnější než rekurzivní, protože rekurzivní modely při složených predikcích chybou při předávání předchozích prognóz zpět do modelu. Pokud jsou zahrnuty funkce prodlevy, AutoML provede některé důležité změny trénovacích dat, aby regresní modely mohly fungovat jako přímé prognostiky. Další podrobnosti najdete v článku o funkcích prodlevy .

Prognózování modelů v AutoML

Následující tabulka uvádí modely prognózování implementované v AutoML a jejich kategorii:

Modely časových řad Regresní modely
Naive, Seasonal Naive, Average, Seasonal Average, Seasonal Average, ARIMA(X), Exponential Smoothing Lineární SGD, LARS LASSO, Elastic Net, Prorok, K Nearest Neighbors, Decision Tree, Random Forest, Extremely Randomized Trees, Gradient Boosted Trees, LightGBM, XGBoost, TCNForecaster

Modely v každé kategorii jsou uvedeny zhruba v pořadí podle složitosti vzorů, které jsou schopny začlenit, označované také jako kapacita modelu. Model Naive, který jednoduše předpovídá poslední pozorovanou hodnotu, má nízkou kapacitu, zatímco dočasná konvoluční síť (TCNForecaster), což je hloubková neurální síť s potenciálně miliony upravitelných parametrů, má vysokou kapacitu.

Důležité je, že AutoML obsahuje také kompletové modely, které vytvářejí vážené kombinace modelů s nejlepším výkonem, aby se dále zlepšila přesnost. Pro prognózování používáme měkký hlasovací soubor , kde se složení a váhy nacházejí prostřednictvím algoritmu výběru souboru Caruana Ensemble.

Poznámka

Pro skupiny předpovědí modelu existují dvě důležitá upozornění:

  1. TCN nelze v současné době zahrnout do souborů.
  2. AutoML ve výchozím nastavení zakáže jinou metodu souboru, soubor zásobníku, který je součástí výchozích regresních a klasifikačních úloh v AutoML. Soubor zásobníku odpovídá metamodelu nejlepších modelových předpovědí, aby se zjistily hmotnosti souboru. V interním srovnávacím testu jsme zjistili, že tato strategie má zvýšenou tendenci překonávat data časových řad. To může mít za následek špatnou generalizaci, takže soubor zásobníku je ve výchozím nastavení zakázaný. V případě potřeby ho ale můžete povolit v konfiguraci automatizovaného strojového učení.

Jak AutoML používá vaše data

AutoML přijímá data časových řad v tabulkovém, "širokém" formátu; to znamená, že každá proměnná musí mít svůj vlastní odpovídající sloupec. AutoML vyžaduje, aby jeden ze sloupců byl časovou osou problému prognózy. Tento sloupec musí být parsovatelný na typ datetime. Nejjednodušší datová sada časových řad se skládá ze sloupce času a číselného cílového sloupce. Cíl je proměnná, která má předpovědět do budoucnosti. Následuje příklad formátu v tomto jednoduchém případě:

časové razítko quantity
2012-01-01 100
2012-01-02 97
2012-01-03 106
... ...
2013-12-31 347

Ve složitějších případech můžou data obsahovat další sloupce odpovídající indexu času.

časové razítko Skladová jednotka (SKU) price Inzerované quantity
2012-01-01 JUICE1 3,5 0 100
2012-01-01 BREAD3 5.76 0 47
2012-01-02 JUICE1 3,5 0 97
2012-01-02 BREAD3 5.5 1 68
... ... ... ... ...
2013-12-31 JUICE1 3,75 0 347
2013-12-31 BREAD3 5.7 0 94

V tomto příkladu je skladová položka, maloobchodní cena a příznak označující, jestli byla položka inzerována kromě časového razítka a cílového množství. Tato datová sada zjevně obsahuje dvě řady – jednu pro SKU JUICE1 a druhou pro SKU BREAD3; sloupec SKU je sloupec ID časové řady , protože seskupení podle něj poskytuje dvě skupiny obsahující jednu řadu. Před tím, než autoML zamete modely, provede základní ověření konfigurace vstupu a dat a přidá technické funkce.

Požadavky na délku dat

Pokud chcete vytrénovat model prognózy, musíte mít dostatečné množství historických dat. Množství této prahové hodnoty se liší podle konfigurace trénování. Pokud jste zadali ověřovací data, minimální počet trénovacích pozorování požadovaných pro jednotlivé časové řady je dán

$T_{\text{ověření uživatele}} = H + \text{max}(l_{\text{max}}, s_{\text{window}}) + 1$,

kde $H$ je horizont prognózy, $l_{\text{max}}$ je pořadí maximální prodlevy a $s_{\text{window}}$ je velikost okna pro funkce průběžné agregace. Pokud používáte křížové ověřování, minimální počet pozorování je:

$T_{\text{CV}} = 2H + (n_{\text{CV}} - 1) n_{\text{step}} + \text{max}(l_{\text{max}}, s_{\text{window}}) + 1$,

kde $n_{\text{CV}}$ je počet záhybů křížového ověření a $n_{\text{step}}$ je velikost kroku CV nebo posun mezi přeložením CV. Základní logika těchto vzorců spočívá v tom, že byste vždy měli mít alespoň horizont trénovacích pozorování pro každou časovou řadu, včetně odsazení pro prodlevy a rozdělení křížového ověření. Další podrobnosti o křížové ověřování pro prognózování najdete v tématu Výběr modelu prognózy .

Zpracování chybějících dat

Modely časových řad automatizovaného strojového učení vyžadují pravidelná pozorování v čase. Pravidelné řádkování zde zahrnuje případy, jako jsou měsíční nebo roční pozorování, kdy se počet dnů mezi pozorováními může lišit. Před modelováním musí AutoML zajistit, že nechybí hodnoty řad a že jsou pozorování pravidelná. Proto chybí dva případy dat:

  • Chybí hodnota pro některé buňky v tabulkových datech.
  • Chybí řádek , který odpovídá očekávanému pozorování s ohledem na frekvenci časových řad.

V prvním případě AutoML chybějící hodnoty zatěžuje běžnými konfigurovatelnými technikami.

Příklad chybějícího očekávaného řádku je uveden v následující tabulce:

časové razítko quantity
2012-01-01 100
2012-01-03 106
2012-01-04 103
... ...
2013-12-31 347

Tato série má zdánlivě denní frekvenci, ale pro 2. ledna 2012 neexistuje žádné pozorování. V takovém případě se AutoML pokusí vyplnit data přidáním nového řádku pro 2. ledna 2012. Nová hodnota quantity sloupce a všechny ostatní sloupce v datech se pak načte jako ostatní chybějící hodnoty. Je zřejmé, že AutoML musí znát frekvenci řad, aby bylo možné vyplnit mezery pozorování, jako je tento. AutoML tuto frekvenci automaticky zjistí, případně ji uživatel může zadat v konfiguraci.

Metodu imputace pro vyplnění chybějících hodnot je možné nakonfigurovat ve vstupu. Výchozí metody jsou uvedeny v následující tabulce:

Typ sloupce Default Imputation – metoda
Cíl Dopředná výplň (poslední přenesená pozorování)
Číselná funkce Medián hodnoty

Chybějící hodnoty pro kategorické funkce jsou během číselného kódování zpracovány zahrnutím další kategorie odpovídající chybějící hodnotě. Imputace je v tomto případě implicitní.

Automatizovaná příprava funkcí

AutoML obecně přidává do uživatelských dat nové sloupce, aby se zvýšila přesnost modelování. Navržená funkce může zahrnovat následující:

Skupina funkcí Výchozí/volitelné
Funkce kalendáře odvozené z časového indexu (například den v týdnu) Výchozí
Kategorické funkce odvozené z ID časových řad Výchozí
Kódování kategorických typů na číselný typ Výchozí
Funkce ukazatelů pro svátky spojené s danou zemí nebo oblastí Volitelné
Prodlevy cílového množství Volitelné
Prodlevy sloupců funkcí Volitelné
Agregace posuvného okna (například klouzavý průměr) cílového množství Volitelné
Sezónní rozklad (STL) Volitelné

Funkcionalizaci můžete nakonfigurovat ze sady SDK autoML prostřednictvím třídy ForecastingJob nebo z webového rozhraní studio Azure Machine Learning.

Detekce a zpracování nestacionárních časových řad

Časová řada, kde se průměr a rozptyl mění v průběhu času, se nazývá nestacionární. Například časové řady, které vykazují stochastické trendy, jsou ze své podstaty nestacionární. Abychom si to vizualizovali, následující obrázek znázorňuje řadu, která má obecně vzestupnou tendenci. Teď vypočítáte a porovnejte střední (průměr) hodnoty pro první a druhou polovinu série. Jsou stejné? Tady je průměr řady v první polovině grafu výrazně menší než v druhé polovině. Skutečnost, že průměr řady závisí na časovém intervalu, na který se člověk dívá, je příkladem časově proměnlivých momentů. Tady je průměr série prvním okamžikem.

Diagram znázorňující maloobchodní prodej pro nestacionární časovou řadu

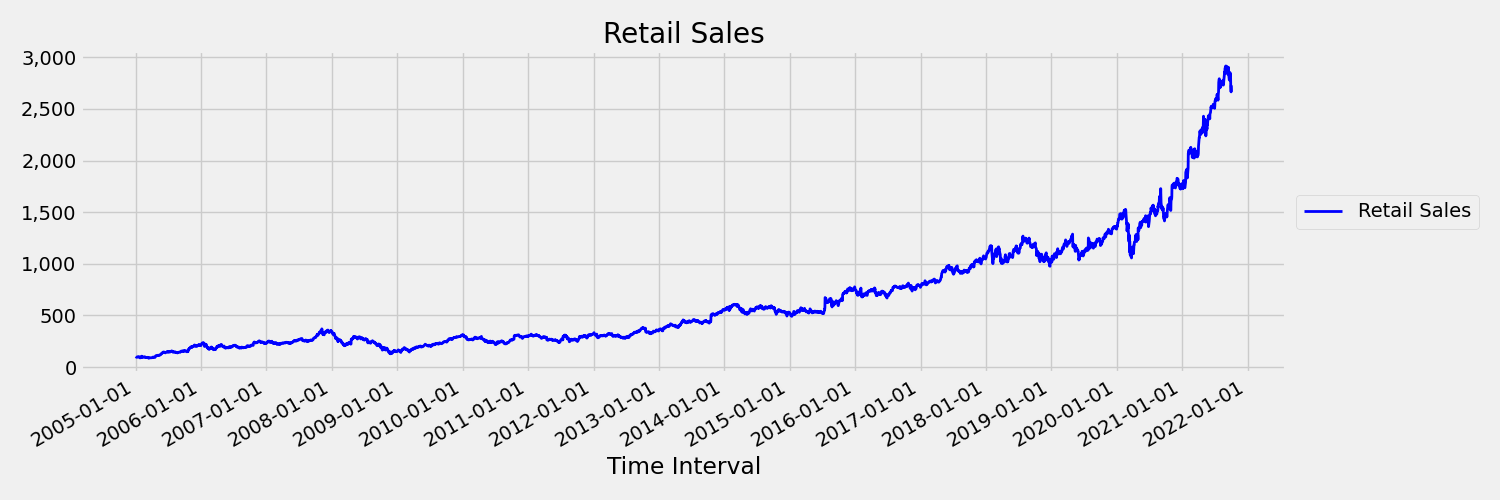
Teď se podíváme na následující obrázek, který vykreslí původní řadu s prvními rozdíly: $\Delta y_{t} = y_t - y_{t-1}$. Průměr řady je v časovém rozsahu zhruba konstantní, zatímco rozptyl se zdá být různý. Toto je tedy příklad statické řady časů prvního řádu.

Diagram znázorňující maloobchodní prodej pro slabě nehybnou časovou řadu

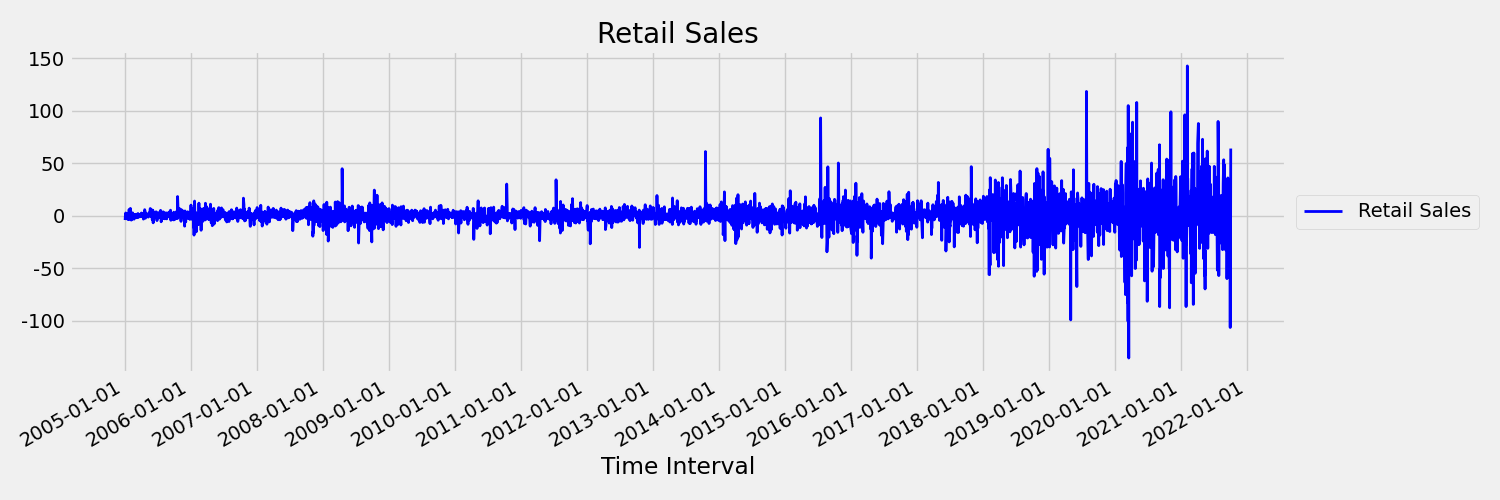
Regresní modely Automatizovaného strojového učení nedokážou ze své podstaty řešit stochastické trendy nebo jiné dobře známé problémy spojené s nestacionárními časovými řadami. V důsledku toho může být přesnost předpovědí mimo vzorky nízká, pokud se takové trendy vyskytují.

AutoML automaticky analyzuje datovou sadu časových řad za účelem určení neměnnosti. Při zjištění nestacionárních časových řad autoML automaticky použije rozdílovou transformaci, aby se zmírnil dopad nestacionárního chování.

Zametání modelů

Po přípravě dat s chybějícím zpracováním dat a přípravou funkcí autoML pomocí služby doporučení modelu přetáhne sadu modelů a hyperparametry. Modely jsou seřazené na základě metrik ověřování nebo křížového ověřování a pak se volitelně můžou nejvyšší modely použít v modelu souboru. Nejlepší model nebo kterýkoli z natrénovaných modelů je možné podle potřeby zkontrolovat, stáhnout nebo nasadit, aby se vytvořily prognózy. Další podrobnosti najdete v článku o úklidu a výběru modelů .

Seskupení modelů

Pokud datová sada obsahuje více než jednu časovou řadu, jako v daném příkladu dat, existuje několik způsobů, jak tato data modelovat. Můžeme například jednoduše seskupovat podle sloupců ID časové řady a trénovat nezávislé modely pro každou řadu. Obecnější přístup je rozdělit data do skupin, které mohou obsahovat více, pravděpodobně souvisejících řad, a trénovat model pro skupinu. Prognózování AutoML ve výchozím nastavení používá k seskupování modelů smíšený přístup. Modely časových řad plus ARIMAX a Prorok přiřazují jednu řadu k jedné skupině a jiné regresní modely přiřazují všechny řady k jedné skupině. Následující tabulka shrnuje seskupení modelů ve dvou kategoriích: 1:1 a M:1:

Každá řada ve vlastní skupině (1:1) Všechny řady v jedné skupině (N:1)
Naive, Sezónní Naive, Průměr, Sezónní průměr, Exponenciální vyhlazování, ARIMA, ARIMAX, Prorok Linear SGD, LARS LASSO, Elastic Net, K Nearest Neighbors, Decision Tree, Random Forest, Extremely Randomized Trees, Gradient Boosted Trees, LightGBM, XGBoost, TCNForecaster

Obecnější seskupení modelů jsou možná prostřednictvím řešení Many-Models AutoML. Podívejte se na článek Řada modelů – Poznámkový blok automatizovaného strojového učení a Hierarchické časové řady – Automatizovaný poznámkový blok ML.

Další kroky