Konvence diagramů kvantových obvodů

Někdy jsou kvantové algoritmy snadněji pochopitelné v diagramu obvodu než v ekvivalentní písemné maticové reprezentaci. Tento článek vysvětluje, jak číst diagramy kvantových obvodů a jejich konvence.

Další informace najdete v tématu Vizualizace diagramů kvantových obvodů.

Čtení diagramů kvantových obvodů

V kvantovém okruhu čas proudí zleva doprava. Kvantové brány jsou seřazeny zleva doprava, přičemž levá brána je první, která je použita na qubity.

Jako příklad použijte následující diagram kvantového obvodu:

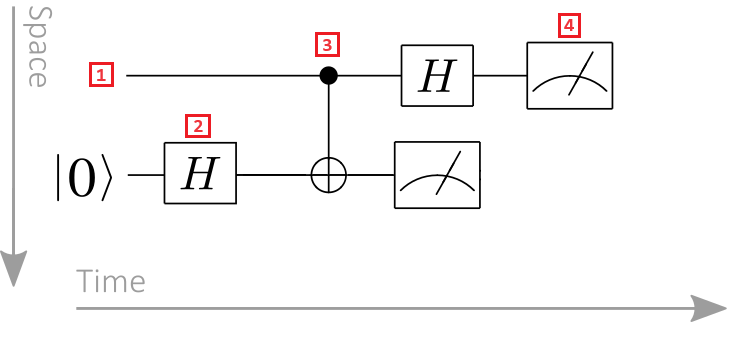
1. Qubitový registr: Qubitové registry se zobrazují jako vodorovné čáry, přičemž každý řádek představuje qubit. Horní řádek je qubitový registr označený číslem 0, druhý řádek je qubitový registr označený číslem 1 a tak dále.
2. Kvantová brána: Kvantové operace jsou reprezentovány kvantovými branami. Pojem kvantové brány je podobný klasickým logickým branám. Brány fungující na jednom nebo více registrech qubitů jsou označeny jako krabice. V tomto příkladu symbol představuje operaci Hadamard.
3. Řízená brána: Řízené brány fungují na dvou nebo více qubitech. V tomto příkladu symbol představuje bránu CNOT. Černý kruh představuje řídicí qubit a kříž uvnitř kruhu target představuje qubit.
4. Měrná operace: Symbol měřiče představuje měrnou operaci. Operace měření přebírá qubitový registr jako vstup a výstupem jsou klasické informace.

Použití kvantových bran

Vzhledem k tomu, že čas plyne zleva doprava, použije se nejprve levá brána. Například akce následujícího kvantového okruhu je matice jednotky $CBA$.

Poznámka:

Násobení matice dodržuje opačnou konvenci: nejprve se použije matice, která je nejvíce napravo. V diagramech kvantových obvodů se však jako první použije levá brána. Tento rozdíl může občas vést k nejasnostem, takže je důležité si uvědomit tento významný rozdíl mezi lineární algebraickou notací a diagramy kvantových obvodů.

Vstupy a výstupy kvantových obvodů

V diagramu kvantového obvodu dráty vstupující do kvantové brány představují qubity, které jsou vstupem do kvantové brány, a dráty ukončující kvantovou bránu představují qubity, které jsou výstupem z kvantové brány.

Počet vstupů kvantové brány se rovná počtu výstupů kvantové brány. Důvodem je to, že kvantové operace jsou unitární a proto reverzibilní. Pokud by kvantová brána měla více výstupů než vstupy, nebyla by nevratná, a proto by nebyla jednotná, což je rozpor.

Z tohoto důvodu musí mít každý box nakreslený v diagramu obvodu přesně stejný počet drátů, které do něj vstupují, jako těch, které z něj vystupují.

Operace s více qubity

Diagramy okruhů s více qubity se řídí podobnými konvencemi jako jedno qubitové. Například dvou qubitovou jednotkovou operaci $B$ je možné definovat tak, aby byla $(H S\otimes X),$ takže ekvivalentní kvantový okruh je následující:

B můžete také považovat $$ za působící na jednom registru se dvěma qubity spíše než na dvou jedniqubitových registrech v závislosti na kontextu, ve kterém se okruh používá.

Nejužitečnější vlastností takových abstraktních diagramů obvodů je, že umožňují popsat složité kvantové algoritmy na vysoké úrovni, aniž by je bylo nutné kompilovat na základní brány. To znamená, že můžete získat přehled o toku dat pro velký kvantový algoritmus, aniž byste museli pochopit všechny podrobnosti o tom, jak jednotlivé podprogramy v rámci algoritmu fungují.

Řízené brány

Kvantové řízené brány jsou dvouqubitové brány, které aplikují bránu na qubit s jedním qubitem target, pokud je řídicí qubit v určitém stavu.

Představte si například kvantovou řízenou bránu označenou $\Lambda(G)$, kde hodnota jednoho qubitu řídí použití operace $G$. Kontrolovaná brána $\Lambda(G)$ se dá pochopit v následujícím příkladu vstupu stavu produktu:

$$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi}+ G \beta\ket{{1}\ket{\psi}$$

To znamená, že kontrolovaná brána použije $G$ na registr obsahující $\psi$ , pokud a pouze v případě, že řídicí qubit vezme hodnotu $1$. Obecně platí, že tyto řízené operace jsou popsány v diagramech obvodů pomocí následujícího symbolu:

Tady černý kruh označuje kvantový bit, na kterém je brána řízená, a svislý drát označuje jednotku, která se použije, když řídicí qubit převezme hodnotu $1$.

Ve zvláštních případech, kdy $G=X$ a $G=Z$ se používá následující zápis k popisu řízené verze bran (všimněte si, že kontrolovaná brána X je brána CNOT):

Q# poskytuje metody pro automatické generování řízené verze operace, která šetří programátora, aby musel tyto operace ručně kódovat. Příklad je uvedený níže:

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

Klasicky řízené brány

Kvantové brány lze použít také po měření, kde výsledek měření funguje jako klasický řídicí bit.

Následující symbol představuje klasicky řízenou bránu, kde $G$ je aplikovaná podmíněně, že klasický řídicí bit má hodnotu $1$:

Operátor měření

Operace měření vezmou qubitový registr, jej změří a výsledek vypíše jako klasickou informaci.

Měrná operace je označená symbolem měřiče a vždy přebírá jako vstup qubitový registr (označený plnou čárou) a výstupy klasických informací (označených dvojitou čárou). Konkrétně symbol operace měření vypadá takto:

Operátor Measure implementuje měřicí operaci v Q#.

Příklad: Unitární transformace

Zvažte jednotkovou transformaci $\text{CNOT}_{01}(H\otimes 1)$. Tato sekvence bran má pro kvantové výpočty zásadní význam, protože vytváří maximálně zapletený dvouqubitový stav.

$$\text{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}} (\ket{{00} + \ket{11})$$

Operace s touto nebo větší složitostí jsou všudypřítomné v kvantových algoritmech a opravách kvantových chyb.

Diagram obvodu pro přípravu tohoto maximálně propleteného kvantového stavu je:

Symbol za bránou Hadamard představuje bránu CNOT, kde černý kruh označuje řídicí qubit a kříž uvnitř kruhu target označuje qubit. Tento kvantový obvod je znázorněn jako působící na dvou kvbitech (nebo na dvou registrech, z nichž každý se skládá z jednoho kvbitu).

Příklad: Diagram teleportačního okruhu

Kvantová teleportace je jedním z nejlepších kvantových algoritmů pro ilustraci prvků obvodu.

Kvantové teleportace je protokol, který umožňuje přenos kvantového stavu z jednoho qubitu do druhého s pomocí sdíleného propleteného stavu mezi odesílatelem a příjemcem a klasickou komunikací mezi nimi.

Pro účely výuky se odesílatel nazývá Alice, příjemce se nazývá Bob a qubit, který se má teleportovat, se nazývá qubit zprávy. Alice a Bob každý drží jeden qubit a Alice má další qubit, což je qubit zprávy.

Následující diagram okruhu znázorňuje teleportační protokol:

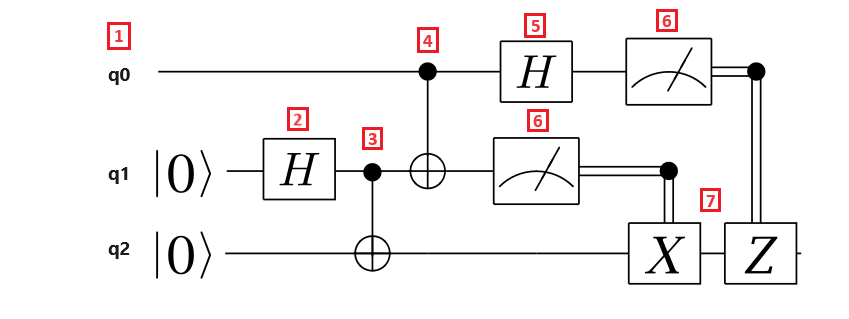
Pojďme si rozdělit kroky teleportačního protokolu:

1. Registr kvantových bitů q0 je qubit zprávy, registr kvantových bitů q1 je Alicein qubit a registr kvantových bitů q2 je Bobův qubit. Qubit zprávy je v neznámém stavu a Alice a Bobovy qubity jsou ve $\ket{0}$ stavu.
2. Hadamardovo hradlo se aplikuje na qubit Alice. Vzhledem k tomu, že qubit je ve $\ket{0}$ stavu, je výsledný stav $\frac{1}{\sqrt{{2}}(\ket{{0} + \ket{1})$.
3. Brána CNOT je aplikována na qubity Alice a Boba. Qubit Alice je řídicí qubit a Qubit Boba je target qubit. Výsledný stav je $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Alice a Bob teď sdílejí propletený stav.
4. Brána CNOT se použije na kvant bitu zprávy a kvant bitu Alice. Vzhledem k tomu, že qubit Alice je také propletený s Bobovým qubitem, výsledný stav je propletený stav se třemi qubity.
5. Hadamardova brána se aplikuje na qubit zprávy.
6. Alice měří své dva qubity a říká výsledky měření Bobovi, což se neprojeví ve schématu. Výsledky měření jsou dva klasické bity, které můžou vzít hodnoty 00, 01, 10 nebo 11.
7. Dvě klasicky řízené Pauli brány X a Z se aplikují na Bobův qubit v závislosti na tom, zda výsledný bit má hodnotu $1$. Výsledný stav je původní stav qubitu zprávy.

Související obsah

• Kvantové propletení
• Groverův algoritmus
• Kvantová střední reprezentace
• Vektory a matice