Teorie Groverova vyhledávacího algoritmu

V tomto článku najdete podrobné teoretické vysvětlení matematických principů, díky kterým Groverův algoritmus funguje.

Praktickou implementaci Groverova algoritmu pro řešení matematických problémů najdete v tématu Implementace Groverova vyhledávacího algoritmu.

Popis problému

Každou úlohu hledání lze vyjádřit pomocí abstraktní funkce $f(x),$ která přijímá hledané položky $x$. Pokud je položka $x$ řešením úlohy hledání, pak $f(x)=1$. Pokud položka $x$ není řešením, pak $f(x)=0$. Problém hledání spočívá v vyhledání libovolné položky$, x_0$ například $f(x_0)=1$.

Úkol, který se Groverův algoritmus snaží vyřešit, může být vyjádřen takto: vzhledem ke klasické funkci $f(x):\{0,1\}^n \rightarrow\{0,1\}$, kde $n$ je bitová velikost vyhledávacího prostoru, vyhledejte vstupní $x_0$ , pro který $f(x_0)=1$. Složitost algoritmu se měří počtem použití funkce $f(x).$ Klasicky, v nejhorším případě, $f(x)$ musí být vyhodnocen celkem $N-1$ krát, kde $N=2^n$, vyzkoušet všechny možnosti. Za $prvky N-1$ musí být poslední prvek. Groverův kvantový algoritmus dokáže tento problém vyřešit mnohem rychleji, což zajistí kvadratickou rychlost. Kvadratická z toho vyplývá, že by se ve srovnání s $N$ vyžadovalo pouze $\sqrt{}$ N hodnocení.

Náčrt algoritmu

Předpokládejme, že pro úkol hledání existuje $N=2^n$ způsobilých položek a tyto položky jsou indexovány přiřazením celého čísla od $0$ do $N-1$. Dále předpokládejme, že existují $různé platné vstupy M$ , což znamená, že existují $vstupy M$ , pro které $f(x)=1$. Kroky algoritmu jsou pak následující:

1. Začněte s registrem $n$ qubitů inicializovaných ve stavu $\ket{0}$.
2. Připravte registr na jednotnou superpozici použitím $H$ na každý qubit registru: $$|\text{zaregistrujte}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x.\rangle$$
3. U registru $použijte následující operace N_{\text{optimální}}$ časy:
   1. Orákulum $fází O_f$ , který pro položky řešení použije podmíněný posun $fáze -1$ .
   2. Použijte $H$ na každý qubit v registru.
   3. Podmíněný fázový posun o $hodnotě -1$ do každého výpočetního základního stavu s výjimkou $\ket{0}$. To může být reprezentováno jednotkovou operací $-O_0$, protože $O_0$ představuje pouze podmíněný fázový posun.$\ket{0}$
   4. Použijte $H$ na každý qubit v registru.
4. Změřte registr a získejte index položky, která je řešením s velmi vysokou pravděpodobností.
5. Zkontrolujte, jestli se jedná o platné řešení. Pokud ne, spusťte znovu.

$\text{N_optimal=}\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{2}\frac{1}{\right\rfloor$ je optimální počet iterací, které maximalizují pravděpodobnost získání správné položky měřením registru.

Poznámka

Společné použití kroků 3.b, 3.c a 3.d je v odborném textu obvykle známo jako Groverův operátor difúze.

Celková jednotná operace použitá pro registr je:

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

Krok za krokem za stavem registru

Abychom tento proces ilustrovali, podívejme se na matematické transformace stavu registru pro jednoduchý případ, ve kterém jsou pouze dva qubity a platný prvek je $\ket{01}.$

1. Registrace začíná ve stavu: $$|\text{register}\rangle=|00\rangle$$

2. Po použití $H na každý qubit se stav registru transformuje na: $$|\text{register}\rangle{1}{\sqrt{=\frac{\sum{4}}_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+)\ket{11}$$$

3. Pak se použije orákulum fáze pro získání: $$|\text{registrace\frac}\rangle=12(\ket{{00}-\ket{{01}+\ket{{10}+)\ket{{11}$$

4. Pak $H$ znovu působí na každý qubit a dá: $$|\text{zaregistrovat}\rangle=\frac12(\ket{{00}+\ket{{01}-{10}\ket{+)\ket{{11}$$

5. Nyní se podmíněný fázový posun použije pro každý stav s výjimkou $\ket{00}$: $$|\text{zaregistrovat}\rangle\frac=12(\ket{{00}-\ket{{01}+{10}\ket{-)\ket{{11}$$

6. Nakonec první iterace Grover končí opětovným použitím $H$ , abyste získali: $$|\text{register}\rangle=\ket{{01}$$

   Při použití výše uvedených kroků se platná položka najde v jedné iteraci. Jak uvidíte později, je to proto, že pro N=4 a jednu platnou položku $N_\text{optimální}=1$.

Geometrické vysvětlení

Abychom zjistili, proč Groverův algoritmus funguje, podívejme se na algoritmus z geometrické perspektivy. Nechť $\ket{\text{je špatná}}$ superpozice všech stavů, které nejsou řešením problému hledání. Za předpokladu, že existují $platná řešení jazyka M$ :

$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

$\ket{\text{Stavový stav je}}$ definován jako superpozice všech stavů, které jsou řešením problému hledání:

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

Vzhledem k tomu , že dobré a špatné jsou vzájemně se vylučující sady, protože položka nemůže být platná a neplatná, jsou stavy $\ket{\text{dobré}}$ a $\ket{\text{špatné}}$ orthogonální. Oba stavy tvoří orthogonální základ roviny v prostoru vektoru. Tuto rovinu můžete použít k vizualizaci algoritmu.

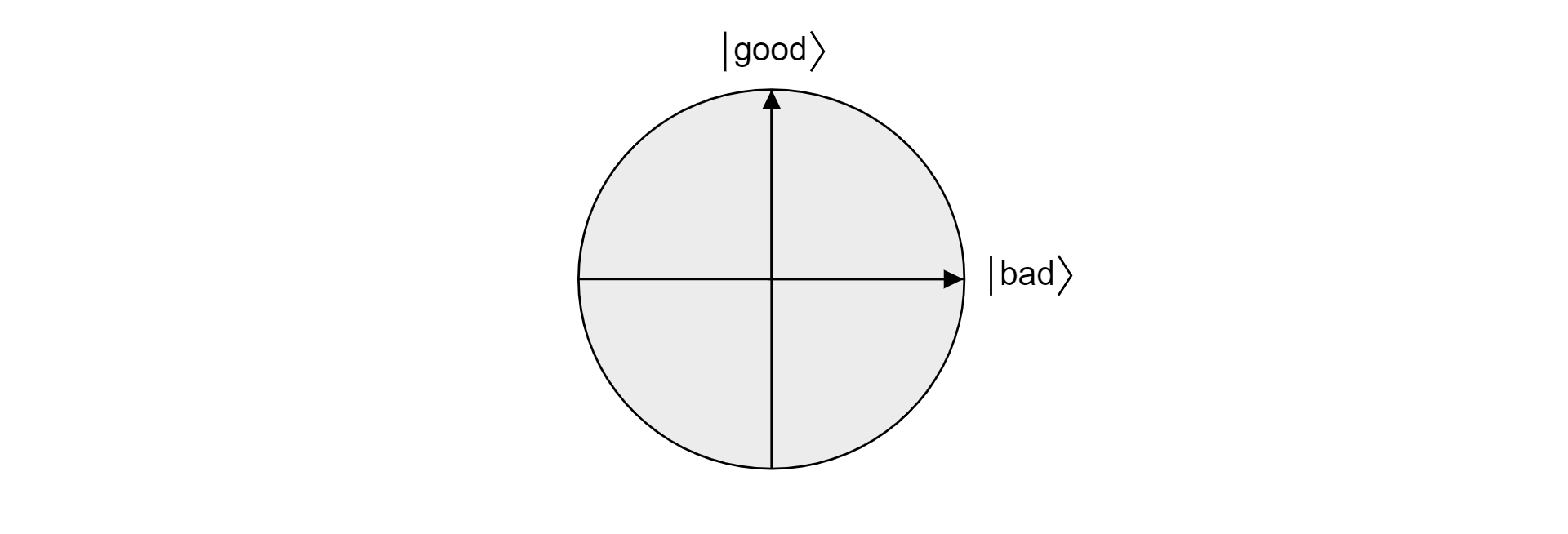
Předpokládejme, že $\ket{\psi}$ je libovolný stav, který žije v rovině, která $\ket{\text{je rozložena dobra}}$ i $\ket{\text{zlého}}$. Každý stát žijící v této rovině může být vyjádřen takto:

$$\ket{\psi}=\alpha\ket{\text{dobré}} + \beta\ket{\text{špatné}}$$

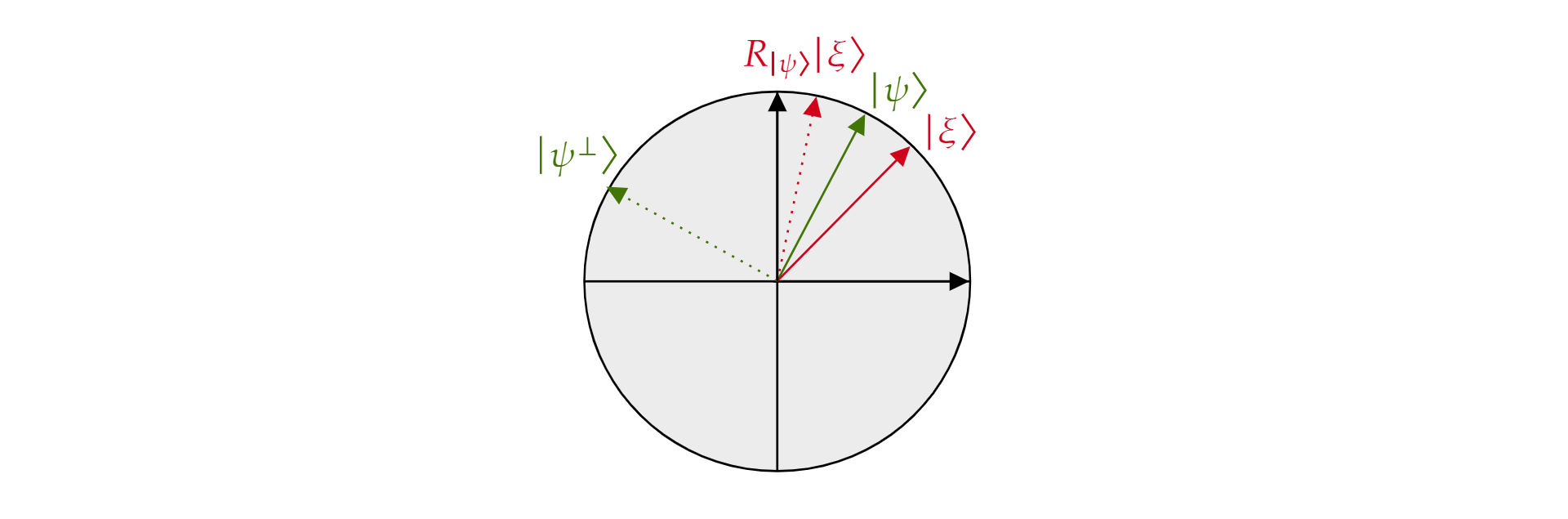
kde $\alpha$ a $\beta$ jsou reálná čísla. Teď si představíme operátor $reflexe R_{\ket{\psi}}$, kde je jakýkoli stav qubitu, který $\ket{\psi}$ se nachází v rovině. Operátor je definován jako:

$${\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$

Nazývá se operátor odrazu o $\ket{\psi}$ , protože jej lze geometricky interpretovat jako odraz o směru $\ket{\psi}$. Chcete-li ji vidět, vezměte si orthogonální základ roviny vytvořené $\ket{\psi}$ a její orthogonální doplněk $\ket{\psi^{\perp}}$. Jakýkoliv stav $\ket{\xi}$ roviny může být rozložen v takovém základu:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Pokud použijete operátor $R_{\ket{\psi}}$ na $\ket{\xi}$:

$${\ket{\psi}}\ket{R_\xi}=\mu \ket{\psi} – \nu {\ket{\psi^{\perp}}}$$

Operátor $R_\ket{\psi}$ převrátí orthogonální komponentu na $\ket{\psi}$ , ale ponechá komponentu $\ket{\psi}$ beze změny. $Proto je R_\ket{\psi}$ odrazem o $\ket{\psi}$.

Groverův algoritmus po prvním použití $H$ na každý qubit začíná jednotnou superpozicí všech stavů. To se dá napsat takto:

$$\ket{\text{all}}\sqrt{\frac{=M}{N good}}}}\ket{\text{ + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$

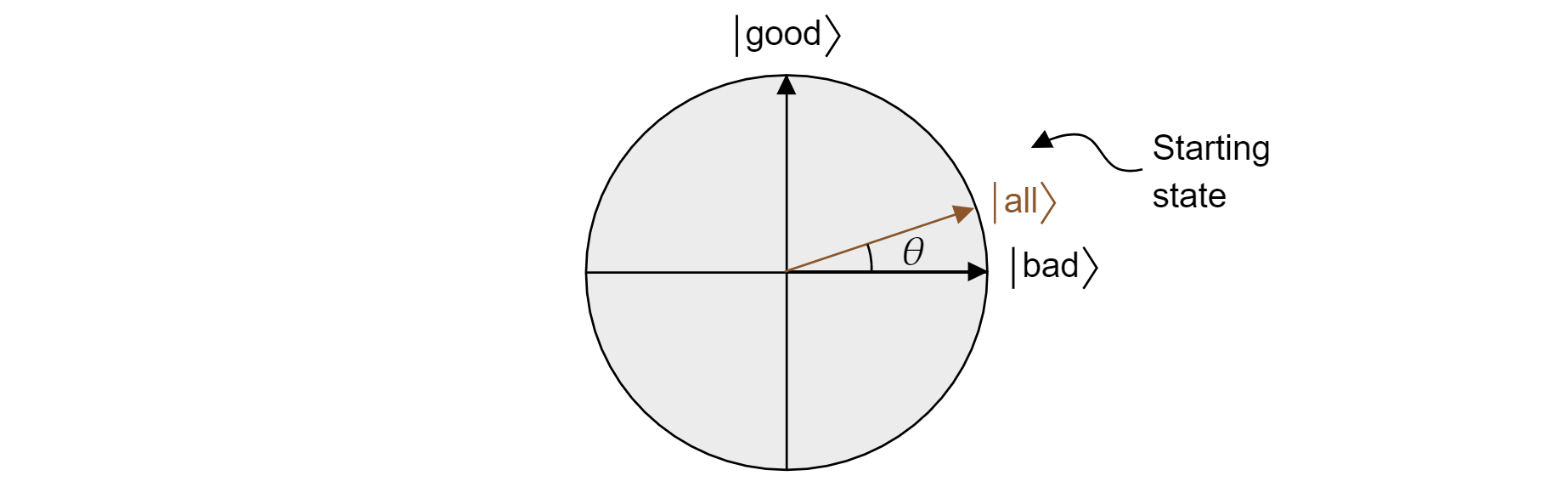
A tak stát žije v letadle. Všimněte si, že pravděpodobnost získání správného výsledku při měření ze stejné superpozice je pouze $|\braket{\text{dobrá}|{\text{}}}|^2=M/N$, což byste očekávali od náhodného odhadu.

Orákulum $O_f$ přidá negativní fázi k jakémukoli řešení problému hledání. Proto může být zapsán jako odraz o $\ket{\text{špatné}}$ ose:

$$= O_f R_{\ket{\text{bad=}}} 2\ket{\text{bad}}\bra{\text{}} - \mathcal{I}$$

Podobně je podmíněný fázový posun $O_0$ jen obrácenou reflexí stavu $\ket{0}$:

$$O_0 R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I =}$$

S vědomím této skutečnosti je snadné ověřit, že Groverova difúzní operace $-H^{\otimes n} O_0 H^{\otimes n}$ je také odrazem stavu $\ket{všech}$. Stačí udělat:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n{0}}\ket{0}\bra{H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}}}\bra{\text{ - \mathcal{I}= R_all{\ket{\text{}}}$$

Bylo prokázáno, že každá iterace Groverova algoritmu je složením dvou odrazů $R_\ket{\text{ a}}$$R_\ket{\text{všechny}}$.

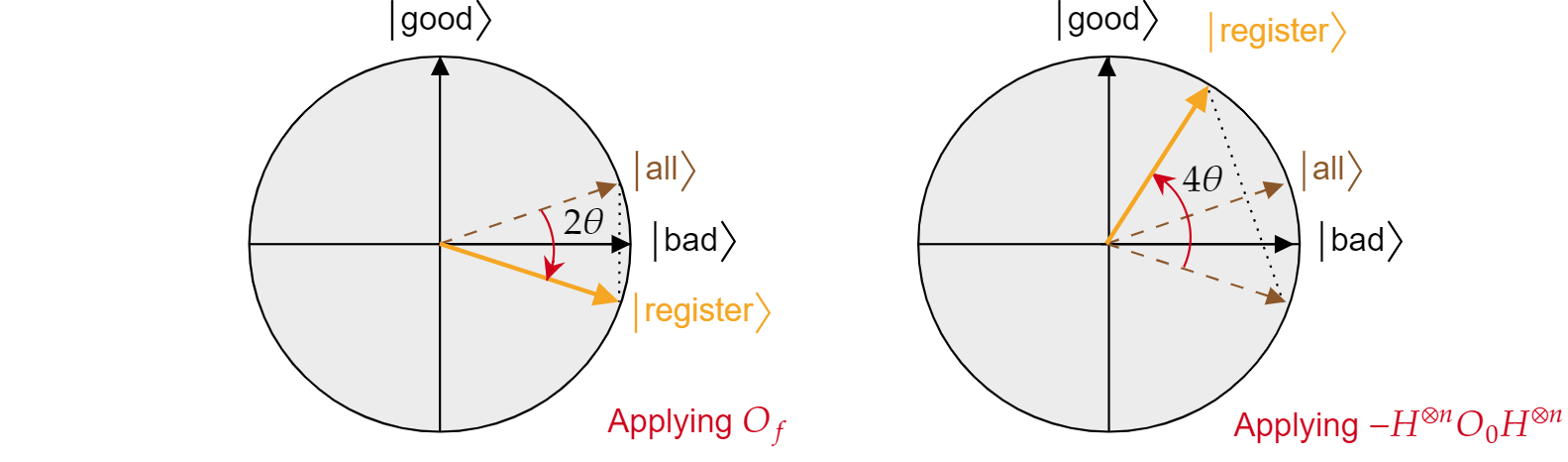
Kombinovaný efekt každé groverové iterace je otočení proti směru hodinových ručiček o úhlu $2\teta$. Naštěstí je úhel $\teta$ snadno najít. Vzhledem k tomu $, že \theta$ je pouze úhel mezi $\ket{\text{všemi}}$ a $\ket{\text{špatnými}}$, můžete k nalezení úhlu použít skalární součin. Je známo, že $\cos{\theta}=\braket{\text{všechny}|\text{špatné}}$, takže je potřeba vypočítat $\braket{\text{všechny}|\text{špatné}}$. Z rozkladu $\ket{\text{všech}}$ z hlediska špatného}}$ a $\ket{\text{dobrého $\ket{\text{}}$to vyplývá:

$$\theta = \arccos{\left(\braket{\text{všechny}|\text{špatné}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

Úhel mezi stavem registru a $\ket{\text{dobrým}}$ stavem se s každou iterací snižuje, což vede k vyšší pravděpodobnosti měření platného výsledku. K výpočtu této pravděpodobnosti stačí vypočítat $|\braket{\text{dobrý}|\text{registr}}|^2$. Označuje úhel mezi $\ket{\text{parametrem good}}$ a $\ket{\text{register$\gamma}}$ (k)$, kde $k$ je počet iterací:

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

Pravděpodobnost úspěchu je proto:

$$P(\text{úspěch}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

Optimální počet iterací

Protože pravděpodobnost úspěchu lze zapsat jako funkci počtu iterací, optimální počet iterací $N_{\text{optimální}}$ lze nalézt výpočtem nejmenšího kladného čísla, které (přibližně) maximalizuje funkci pravděpodobnosti úspěchu.

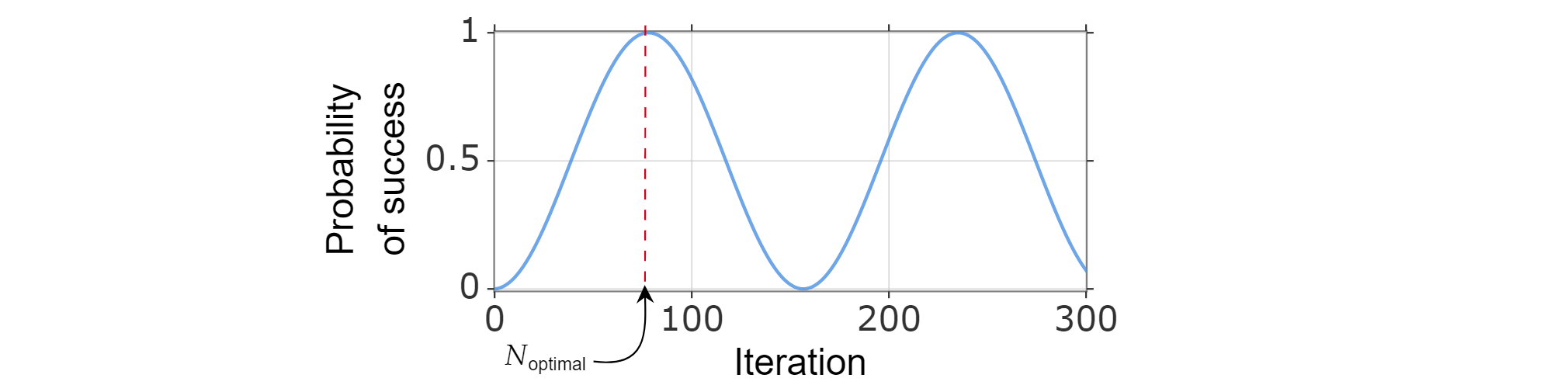
Je známo, že $\sin^2{x}$ dosáhne svého prvního maxima pro $x=\frac{\pi}{2}$, takže:

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Tím získáte:

$${\text{k_optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2\frac{= \pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N)}\right$$

Kde v posledním kroku: $\arccos \sqrt{1-x=\sqrt{}x} + O(x^{3/2})$.

Proto můžete vybrat $N_optimální}$ tak, aby $byla N_\text{optimal=\left}\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{1}{2}\frac{\right\rfloor.$\text{

Analýza složitosti

Z předchozí analýzy $\leftjsou k nalezení platné položky potřeba dotazy O(\sqrt{\frac{N}{M}}\right)$ orákulum $O_f$. Je však možné algoritmus implementovat efektivně z hlediska časové složitosti? $$ O_0 je založená na výpočtu logických operací na $n$ bitech a je známo, že je možné ji implementovat pomocí $bran O(n).$ Existují také dvě vrstvy $n$ Hadamardových bran. Obě tyto komponenty proto vyžadují pouze $brány O(n)$ pro každou iteraci. Protože $N=2^n$, následuje $O(n)=O(log(N))$. Proto pokud $jsou potřeba iterace O\left(\sqrt{\frac{N}{M}}\right)$ a $brány O(log(N))$ pro iteraci, celková časová složitost (bez zohlednění implementace orákulum) je $O\left(\sqrt{\frac{N}{M}}log(N)\right))$).

Celková složitost algoritmu nakonec závisí na složitosti implementace orákulum $O_f$. Pokud je vyhodnocení funkce na kvantovém počítači mnohem složitější než na klasickém počítači, celkový běh algoritmu bude v kvantovém případě delší, i když technicky používá méně dotazů.

Reference

Pokud se chcete dál seznamovat s Groverovým algoritmem, můžete zkontrolovat některý z následujících zdrojů:

• Původní dokument lovu K. Grovera
• Oddíl kvantových vyhledávacích algoritmů v článku Nielsen, M. A. &Amp; Chuang, I. L. (2010). Kvantové výpočty a kvantové informace.
• Groverův algoritmus na Arxiv.org

Další kroky

• Kvantové reprezentace mezilehlých
• Vektory a matice
• T brány a T továrny
• Více qubitů