Role bran T a T v kvantových výpočtech
Tento článek popisuje roli bran T a T továren v kvantových výpočtech odolných proti chybám. Díky kvantovému algoritmu se odhad požadovaných prostředků pro spouštění bran T a továren T stává zásadním faktorem pro určení proveditelnosti algoritmu. Estimátor prostředků Azure Quantum vypočítá počet stavů T potřebných ke spuštění algoritmu, počet fyzických qubitů pro jednu továrnu T a modul runtime objektu pro vytváření T.
Univerzální sada kvantových bran
Podle kritérií DiVincenzo musí být škálovatelný kvantový počítač schopný implementovat univerzální sadu kvantových bran. Univerzální sada obsahuje všechna hradla potřebná k provedení kvantového výpočtu, tj. všechny výpočty se musí rozložit zpět do konečné posloupnosti univerzálních bran. Alespoň kvantový počítač musí být schopný přesouvat jednotlivé qubity na libovolnou pozici na Bloch Sphere (pomocí bran s jedním qubitem), stejně jako zavést propletení v systému, což vyžaduje více qubitovou bránu.
V klasickém počítači jsou pouze čtyři funkce, které mapují jeden bit na jeden bit. Naproti tomu existuje nekonečný počet jednotkových transformací na jednom qubitu na kvantovém počítači. Proto žádná konečná sada primitivních kvantových operací nebo bran nemůže přesně replikovat nekonečnou sadu jednotkových transformací povolených v kvantových výpočtech. To znamená, že na rozdíl od klasického computingu není možné, aby kvantový počítač implementovali všechny možné kvantové programy přesně pomocí konečného počtu bran. Kvantové počítače proto nemohou být univerzální ve stejném smyslu klasických počítačů. Když tedy říkáme, že sada bran je univerzální pro kvantové výpočty, znamenáme ve skutečnosti něco mírně slabšího než u klasického computingu.
Pro univerzálnost je nutné, aby kvantový počítač přibližuje pouze každou jednotkovou matici v rámci konečné chyby pomocí konečné sekvence brány délky.
Jinými slovy, sada bran je univerzální sada bran, pokud jakákoli jednotná transformace může být přibližně napsána jako součin bran z této sady. Vyžaduje se, aby v případě jakékoli předepsané chybové vazby existovaly brány $G_{1}, G_{2}, \ldoty, G_N$ ze sady bran tak, aby
$${G_N G_N-1}\cdots G_2 G_1 \cca U.$$
Vzhledem k tomu, že konvence násobení matic je násobit zprava doleva první bránou operace v této sekvenci, $G_N$ je ve skutečnosti poslední použitou u vektoru kvantového stavu. Formálněji se říká, že taková sada bran je univerzální, pokud pro každou odolnost $proti chybám \epsilon>0$ existuje $G_1, \ldots, G_N$ tak, aby vzdálenost mezi $G_N\ldots G_1$ a $U$ je maximálně $\epsilon$. V ideálním případě by hodnota $N$ potřebná k dosažení této vzdálenosti $\epsilon$ měla škálovat poly-logaritmicky s $hodnotou 1/\epsilon$.
Například sada vytvořená Hadamardem, CNOT a T branami je univerzální sada, ze které lze vygenerovat všechny kvantové výpočty (na libovolném počtu qubitů). Hadamard a sada bran T generuje jakoukoli bránu s jedním qubitem:
$$H=\frac{1}{\sqrt{ 1 amp; 1 \\ 1 &-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.&{2}}\begin{bmatrix} $$
V kvantovém počítači lze kvantové brány klasifikovat do dvou kategorií: Cliffordové brány a brány non-Clifford, v tomto případě brána T. Kvantové programy vytvořené pouze cliffordovými branami lze efektivně simulovat pomocí klasického počítače, a proto jsou k získání kvantové výhody vyžadovány brány non-Clifford. V mnoha kvantových opravách chyb (QEC) schématu tzv. Cliffordových bran se snadno implementují, to znamená, že vyžadují velmi málo prostředků z hlediska operací a qubitů k implementaci chyb odolných proti chybám, zatímco brány, které nejsou Cliffordem, jsou při vyžadování odolnosti proti chybám poměrně nákladné. V univerzální kvantové sadě se brána T běžně používá jako brána non-Clifford.
Standardní sada jedno qubitových cliffordových bran zahrnutých ve výchozím nastavení Q#, včetně
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$ Y =\begin{bmatrix} 0 & -i \\ & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&-1 \end{bmatrix}=T^4. $$
Společně s bránou non-Clifford (brána T) se tyto operace dají skládat, aby se přibližné jakékoli jednotné transformace na jednom qubitu.
T factory in the Azure Quantum Resource Estimator
Příprava brány non-Clifford T je zásadní, protože ostatní kvantové brány nejsou dostatečné pro univerzální kvantové výpočty. K implementaci operací, které nejsou Cliffordem pro algoritmy praktického rozsahu, je vyžadována nízká míra chybových bran T (nebo stavů T). U některých fyzických qubitů ale může být obtížné je přímo implementovat na logických qubitech.
V kvantovém počítači odolném proti chybám se požadované stavy T s nízkou mírou chyb vytvářejí pomocí továrny pro destilování stavu T nebo výroby T pro krátkou dobu. Tyto T továrny obvykle zahrnují posloupnost cyklů destilace, kde každé kolo přebírá mnoho hlučných stavů T kódovaných v menším kódu vzdálenosti, zpracovává je pomocí destilační jednotky a výstupy méně hlučných T stavů kódovaných ve větším kódu vzdálenosti, s počtem kruhových, destilačních jednotek a vzdáleností, které mohou být různé. Tento postup je iterated, kde výstupní T stavy jednoho kola jsou předány do dalšího kola jako vstupy.
Na základě doby trvání objektu pro vytváření T určuje estimátor prostředků Azure Quantum, jak často může být objekt pro vytváření T vyvolán před překročením celkového běhu algoritmu, a tedy počet stavů T, které lze během modulu runtime algoritmu vytvořit. Obvykle se vyžaduje více stavů T, než je možné vytvořit v rámci vyvolání jednoho objektu pro vytváření T během modulu runtime algoritmu. Aby mohl estimátor prostředků vytvořit více stavů T, používá kopie továren T.
Fyzický odhad T factory
Estimátor prostředků vypočítá celkový počet stavů T potřebných ke spuštění algoritmu a počet fyzických qubitů pro jednu továrnu T a jeho modul runtime.
Cílem je vytvořit všechny stavy T v modulu runtime algoritmu s co nejnižším množstvím kopií objektu pro vytváření T. Následující diagram znázorňuje příklad modulu runtime algoritmu a modulu runtime jednoho objektu pro vytváření T. Vidíte, že modul runtime objektu pro vytváření T je kratší než modul runtime algoritmu. V tomto příkladu může jedna továrna T destilovat jeden stav T. Vyvstanou dvě otázky:
- Jak často může být továrna T vyvolána před koncem algoritmu?
- Kolik kopií destilační kruhu T továrny je nutné k vytvoření počtu stavů T požadovaných během běhu algoritmu?
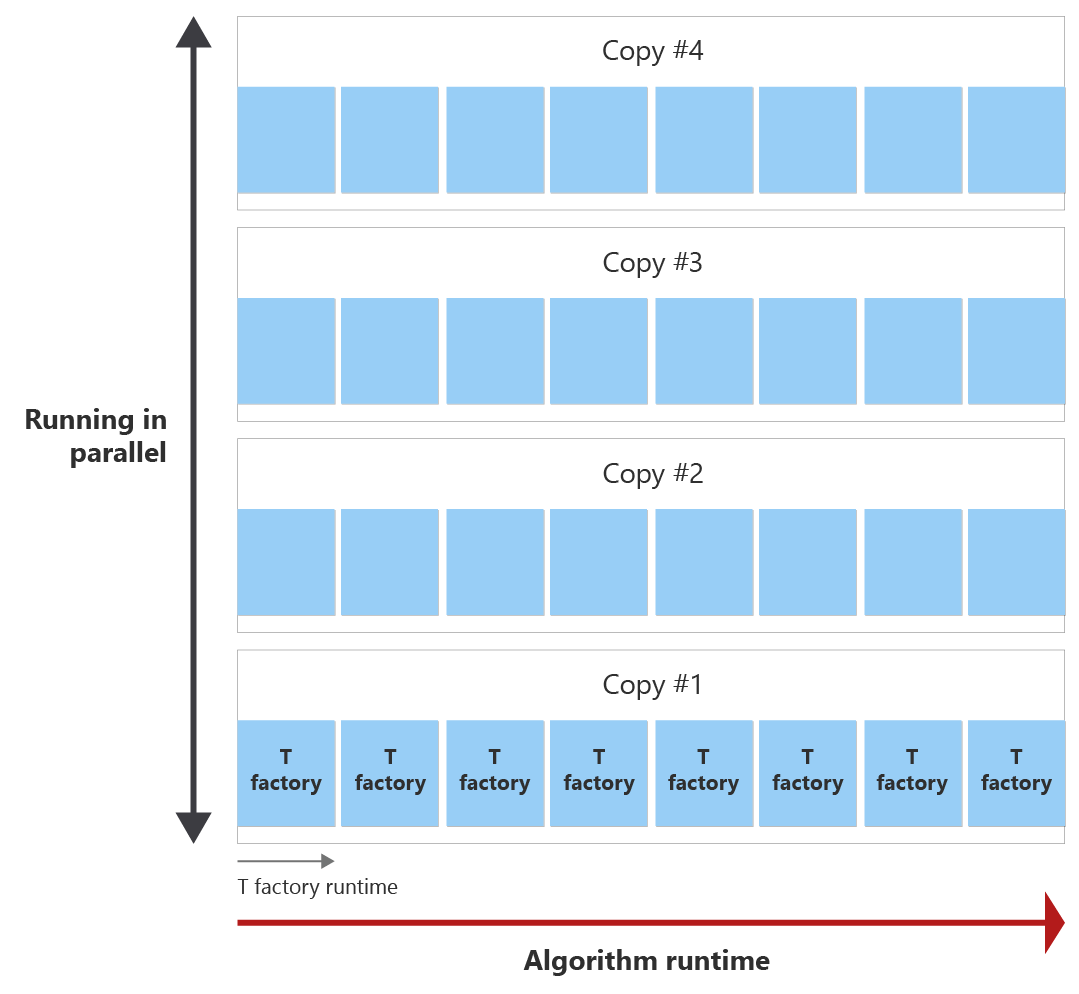
Před koncem algoritmu lze továrnu T vyvolat osmkrát, což se nazývá destilační kruh. Pokud například potřebujete 30 T stavů, vyvolá se jedna továrna T osmkrát během běhu algoritmu, a proto vytvoří osm stavů T. Pak potřebujete čtyři kopie výrobního destilačního kruhu T paralelně pro destilování potřebných 30 T stavů.
Poznámka:
Všimněte si, že kopie objektu pro vytváření T a vyvolání T factory nejsou stejné.
Závody pro destilační výrobu T jsou implementovány v posloupnosti kruhů, kde každé kolo se skládá ze sady kopií destilačních jednotek běžících paralelně. Estimátor prostředků vypočítá, kolik fyzických qubitů je potřeba ke spuštění jedné továrny T a jak dlouho běží mimo jiné požadované parametry.
Můžete provádět pouze úplné vyvolání továrny T. Proto může dojít k situacím, kdy kumulovaný modul runtime všech vyvolání T factory je menší než modul runtime algoritmu. Vzhledem k tomu, že qubity se používají v různých kolech, počet fyzických qubitů pro jednu továrnu T je maximální počet fyzických qubitů používaných pro jedno kolo. Modul runtime objektu pro vytváření T je součet modulu runtime ve všech kolech.
Poznámka:
Pokud je míra chyb fyzické brány T nižší než požadovaná logická míra chyb stavu T, nemůže odhad prostředků provést dobrý odhad prostředků. Když odešlete úlohu odhadu zdrojů, může dojít k tomu, že objekt pro vytváření T nelze najít, protože požadovaná chybovost logického stavu T je příliš nízká nebo příliš vysoká.
Další informace najdete v dodatku C k posouzení požadavků pro škálování na praktickou kvantovou výhodu.