Projektionstransformation (Direct3D 9)

Sie können sich die Projektionstransformation als Steuerung der Internen der Kamera vorstellen; es ist analog zur Auswahl eines Objektivs für die Kamera. Dies ist der komplizierteste der drei Transformationstypen. Diese Diskussion der Projektionstransformation ist in die folgenden Themen unterteilt.

Die Projektionsmatrix ist in der Regel eine Skalierungs- und Perspektivprojektion. Die Projektionstransformation wandelt das Anzeige frustum in eine Quaderform um. Da das nahe Ende des Anzeige frustums kleiner ist als das ferne Ende, hat dies den Effekt, dass sich Objekte erweitern, die sich in der Nähe der Kamera befinden; So wird die Perspektive auf die Szene angewendet.

Im Anzeige frustum wird der Abstand zwischen der Kamera und dem Ursprung des Sichttransformationsraums beliebig als D definiert, sodass die Projektionsmatrix wie in der folgenden Abbildung aussieht.

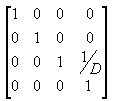
Die Anzeigematrix übersetzt die Kamera in den Ursprung, indem sie in z-Richtung durch - D übersetzt. Die Übersetzungsmatrix entspricht der folgenden Abbildung.

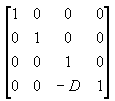
Das Multiplizieren der Übersetzungsmatrix mit der Projektionsmatrix (T*P) ergibt die zusammengesetzte Projektionsmatrix, wie in der folgenden Abbildung dargestellt.

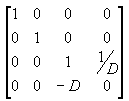
Die perspektivische Transformation wandelt ein Anzeige frustum in einen neuen Koordinatenraum um. Beachten Sie, dass das Frustum zum Quader wird und dass der Ursprung von der rechten oberen Ecke der Szene in die Mitte wechselt, wie im folgenden Diagramm dargestellt.

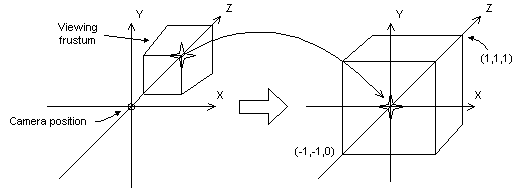
In der Perspektivtransformation sind die Grenzen der x- und y-Richtung -1 und 1. Die Grenzen der Z-Richtung sind 0 für die vordere Ebene und 1 für die Rückebene.

Diese Matrix übersetzt und skaliert Objekte basierend auf einem angegebenen Abstand von der Kamera zur nahen Clippingebene, berücksichtigt jedoch nicht das Sichtfeld (fov), und die Z-Werte, die sie für Objekte in der Entfernung erzeugt, können nahezu identisch sein, was Tiefenvergleiche erschwert. Die folgende Matrix behandelt diese Probleme, und sie passt Scheitelpunkte an, um das Seitenverhältnis des Viewports zu berücksichtigen, sodass er eine gute Wahl für die perspektivische Projektion ist.

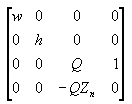
In dieser Matrix ist Zn der Z-Wert der nahen Clippingebene. Die Variablen w, h und Q haben die folgende Bedeutung. Beachten Sie, dass fov_w und fovk die horizontalen und vertikalen Ansichtsfelder des Viewports im Bogenmaß darstellen.

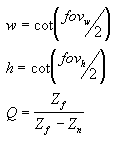
Für Ihre Anwendung ist die Verwendung von Sichtfeldwinkeln zum Definieren der x- und y-Skalierungskoeffizienten möglicherweise nicht so praktisch wie die verwendung der horizontalen und vertikalen Abmessungen des Viewports (im Kamerabereich). Wenn die Mathematik funktioniert, verwenden die folgenden beiden Formeln für w und h die Dimensionen des Viewports und entsprechen den obigen Formeln.

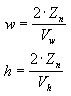
In diesen Formeln stellt Zn die Position der nahen Clippingebene dar, und die Variablen V_w und Vh stellen die Breite und Höhe des Viewports im Kamerabereich dar.

Bei einer C++-Anwendung entsprechen diese beiden Dimensionen direkt den Elementen Width und Height der D3DVIEWPORT9-Struktur .

Unabhängig davon, für welche Formel Sie sich entscheiden, stellen Sie sicher, dass Sie Zn auf einen so großen Wert wie möglich festlegen, da Z-Werte extrem nahe an der Kamera variieren. Dies macht Tiefenvergleiche mit 16-Bit-Z-Puffern etwas kompliziert.

Wie bei den Welt- und Ansichtstransformationen rufen Sie die IDirect3DDevice9::SetTransform-Methode auf, um die Projektionstransformation festzulegen.

Einrichten einer Projektionsmatrix

Die folgende ProjectionMatrix-Beispielfunktion legt die Beschneidungsebenen vorne und hinten sowie das horizontale und vertikale Feld der Ansichtswinkel fest. Die Ansichtsfelder sollten kleiner als pi bogenmaßen sein.

D3DXMATRIX 
ProjectionMatrix(const float near_plane, // Distance to near clipping 
                                         // plane
                 const float far_plane,  // Distance to far clipping 
                                         // plane
                 const float fov_horiz,  // Horizontal field of view 
                                         // angle, in radians
                 const float fov_vert)   // Vertical field of view 
                                         // angle, in radians
{
    float    h, w, Q;

    w = (float)1/tan(fov_horiz*0.5);  // 1/tan(x) == cot(x)
    h = (float)1/tan(fov_vert*0.5);   // 1/tan(x) == cot(x)
    Q = far_plane/(far_plane - near_plane);

    D3DXMATRIX ret;
    ZeroMemory(&ret, sizeof(ret));

    ret(0, 0) = w;
    ret(1, 1) = h;
    ret(2, 2) = Q;
    ret(3, 2) = -Q*near_plane;
    ret(2, 3) = 1;
    return ret;
}   // End of ProjectionMatrix

Nachdem Sie die Matrix erstellt haben, legen Sie sie mit IDirect3DDevice9::SetTransform fest, und geben Sie D3DTS_PROJECTION an.

Die D3DX-Hilfsprogrammbibliothek bietet die folgenden Funktionen, die Ihnen beim Einrichten Ihrer Projektionsmatrix helfen.

• D3DXMatrixPerspectiveLH
• D3DXMatrixPerspectiveRH
• D3DXMatrixPerspectiveFovLH
• D3DXMatrixPerspectiveFovRH
• D3DXMatrixPerspectiveOffCenterLH
• D3DXMatrixPerspectiveOffCenterRH

Eine W-freundliche Projektionsmatrix

Direct3D kann die w-Komponente eines Scheitelpunkts verwenden, der von den Welt-, Ansichts- und Projektionsmatrizen transformiert wurde, um tiefenbasierte Berechnungen in Tiefenpuffer- oder Nebeleffekten durchzuführen. Berechnungen wie diese erfordern, dass Ihre Projektionsmatrix w normalisiert, um dem Weltraum z zu entsprechen. Kurz gesagt, wenn Ihre Projektionsmatrix einen (3,4) Koeffizienten enthält, der nicht 1 ist, müssen Sie alle Koeffizienten um die Umkehrung des Koeffizienten (3,4) skalieren, um eine richtige Matrix zu erstellen. Wenn Sie keine kompatible Matrix bereitstellen, werden Nebeleffekte und Tiefenpufferung nicht ordnungsgemäß angewendet.

Die folgende Abbildung zeigt eine nicht konforme Projektionsmatrix und dieselbe Matrix, die skaliert ist, sodass augenbezogener Nebel aktiviert wird.

In den vorangehenden Matrizen wird angenommen, dass alle Variablen ungleich null sind. Weitere Informationen zu augenbezogenem Nebel finden Sie unter Augenbezogene und Z-basierte Tiefe. Informationen zur w-basierten Tiefenpufferung finden Sie unter Tiefenpuffer (Direct3D 9).

Direct3D verwendet die derzeit festgelegte Projektionsmatrix in w-basierten Tiefenberechnungen. Daher müssen Anwendungen eine konforme Projektionsmatrix festlegen, um die gewünschten w-basierten Features zu erhalten, auch wenn sie Direct3D für Transformationen nicht verwenden.

Zugehörige Themen

Transformationen