Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
In this quickstart, you learn how to use the Azure Quantum Resource Estimator to estimate the resources of a Q# program.
Prerequisites
- The latest version of Visual Studio Code or open VS Code on the Web.
- The latest version of the Quantum Development Kit extension. For installation details, see Set up the QDK extension.
Tip
You don't need to have an Azure account to run the Resource Estimator.
Load a Q# sample program
- Open Visual Studio Code.
- Select File > New File and save the file as RandomNum.qs.
- Open RandomNum.qs and start typing
sampleto open the dropdown menu of Q# samples. - Select Random Bit sample and save the file again.
Run the Resource Estimator
The Resource Estimator offers six predefined qubit parameters, four of which have gate-based instruction sets and two that have a Majorana instruction set. It also offers two quantum error correction codes, surface_code and floquet_code.
In this example, you run the Resource Estimator using the qubit_gate_us_e3 qubit parameter and the surface_code quantum error correction code.
- Select View -> Command Palette, or press Ctrl+Shift+P, and type “resource” which should bring up the QDK: Calculate Resource Estimates option. Select this option to open the Resource Estimator window.
- You can select one or more Qubit parameter + Error Correction code types to estimate the resources for. For this example, select qubit_gate_us_e3 and click OK.
- Specify the Error budget or accept the default value 0.001. For this example, leave the default value and press Enter.
- Press Enter to accept the default result name based on the filename, in this case, RandomNum.
View the results
The Resource Estimator provides multiple estimates for the same algorithm, each showing tradeoffs between the number of qubits and the runtime. Understanding the tradeoff between runtime and system scale is one of the more important aspects of resource estimation.
The result of the resource estimation is displayed in the Q# Estimate window.
The Results tab displays a summary of the resource estimation. Click the icon next to the first row to select the columns you want to display. You can select from run name, estimate type, qubit type, qec scheme, error budget, logical qubits, logical depth, code distance, T states, T factories, T factory fraction, runtime, rQOPS, and physical qubits.
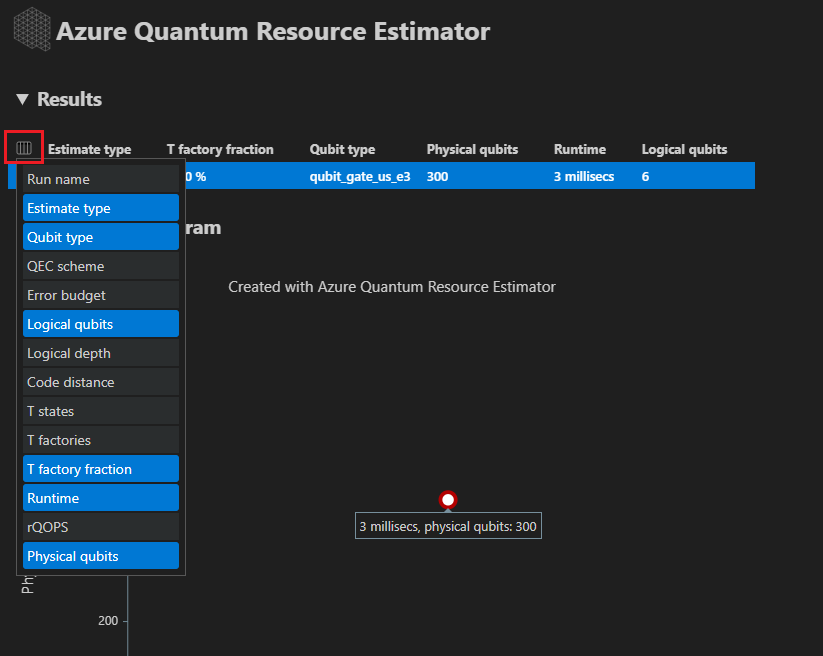
In the Estimate type column of the results table, you can see the number of optimal combinations of {number of qubits, runtime} for your algorithm. These combinations can be seen in the space-time diagram.
Note
If you select more than one qubit parameters and error correction codes in the configuration, the results are displayed in different rows in the Results tab. Clicking on a result from the table brings up the corresponding space diagram and report data.
The Space-time diagram tab shows the tradeoffs between the number of physical qubits and the runtime of the algorithm. In this case, the Resource Estimator finds 1 optimal combination out of many thousands possible ones. You can hover over each {number of qubits, runtime} point to see the details of the resource estimation at that point. For more information, see Space-time diagram.
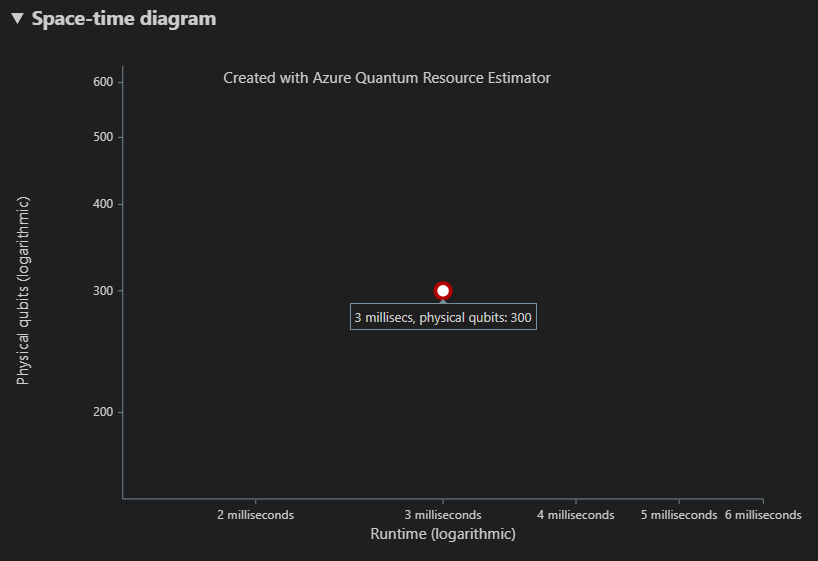
Note
You need to click on one point of the space-time diagram, that is a {number of qubits, runtime} pair, to see the space diagram and the details of the resource estimation corresponding to that point.
The Space diagram tab displays the distribution of physical qubits used for the algorithm and the T factories. In this example, the algorithm qubits and the total qubits are the same because the algorithm does not use any T factory copies. For more information, see Space-time diagrams.
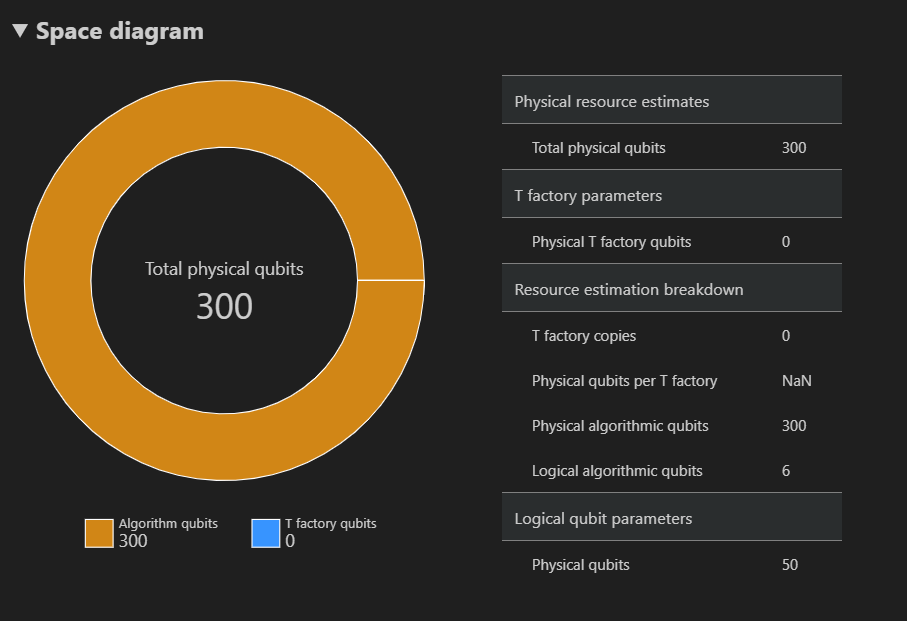
Finally, the Resource Estimates tab displays the full list of output data for the Resource Estimator. You can inspect cost details by collapsing the groups, which have more information. For example, collapse the Logical qubit parameters group. For more information, see the report data of the Resource Estimator for the Resource Estimator.
Logical qubit parameter Value QEC scheme surface_code Code distance 5 Physical qubits 50 Logical cycle time 3 millisecs Logical qubit error rate 3.00E-5 Crossing prefactor 0.03 Error correction threshold 0.01 Logical cycle time formula (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistancePhysical qubits formula 2 * codeDistance*codeDistanceTip
Click Show detailed rows to display the description of each output of the report data.
The full functionality of the Resource Estimator is beyond the scope of this quickstart. For more information, see Use the Resource Estimator with different SDKs and IDEs.
Note
If you run into any issue while working with the Resource Estimator, check out the Troubleshooting page, or contact AzureQuantumInfo@microsoft.com.