Teoría del algoritmo de búsqueda de Grover

En este artículo encontrará una explicación teórica detallada de los principios matemáticos que hacen que el algoritmo de Grover funcione.

Para obtener una implementación práctica del algoritmo de Grover para resolver problemas matemáticos, consulte Implementación del algoritmo de búsqueda de Grover.

Instrucción del problema

Cualquier tarea de búsqueda se puede expresar con una función $f(x)$ abstracta que acepta elementos de búsqueda $x$. Si el elemento $x$ es una solución para la tarea de búsqueda, $f(x)=1$. Si el elemento $x$ no es una solución, $f(x)=0$. El problema de búsqueda consiste en buscar cualquier elemento $x_0$, de forma que $f(x_0)=1$.

La tarea que pretende resolver el algoritmo de Grover puede expresarse de la siguiente manera: dada una función clásica $f(x):\{0,1\}^n \rightarrow\{0,1\}$, donde $n$ es el tamaño de los bits del espacio de búsqueda, encontrar una entrada $x_0$ para la que $f(x_0)=1$. La complejidad del algoritmo se mide por el número de usos de la función $f(x)$. De forma clásica, en el peor de los casos, tenemos que evaluar $f(x)$ un total de $N-1$ veces, donde $N=2^n$, probando todas las posibilidades. Después de $N-1$ elementos, debe ser el último elemento. El algoritmo cuántico de Grover puede resolver este problema mucho más rápido, con una velocidad cuadrática. La velocidad cuadrática implica que solo se requieren $\sqrt{N}$ evaluaciones, en comparación con $N$.

Esquema del algoritmo

Supongamos que hay $N=2^n$ elementos aptos para la tarea de búsqueda y los indexamos asignando a cada elemento un entero de $0$ a $N-1$. Además, supongamos que hay $M$ entradas válidas diferentes, lo que significa que hay $M$ entradas para las que $f(x)=1$. Los pasos del algoritmo son los siguientes:

1. Comience con un registro de $n$ cúbits iniciado en el estado $\ket{0}$.
2. Prepare el registro en una superposición uniforme aplicando $H$ a cada cúbit del registro: $$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
3. Aplique las siguientes operaciones al registro $N_{\text{optimal}}$ veces:
   1. El oráculo de fase $O_f$ que aplica un desplazamiento de fase condicional de $-1$ para los elementos de la solución.
   2. Aplique $H$ a cada cúbit del registro.
   3. Un desplazamiento de fase condicional de $-1$ a cada estado de base computacional excepto $\ket{0}$. Esto se puede representar mediante la operación unitaria $-O_0$, del mismo modo que $O_0$ representa el desplazamiento de la fase condicional a $\ket{0}$ solamente.
   4. Aplique $H$ a cada cúbit del registro.
4. Mida el registro para obtener el índice de un elemento que es una solución con una probabilidad muy alta.
5. Compruebe si se trata de una solución válida. Si no es así, vuelve a empezar.

$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ es el número óptimo de iteraciones que maximiza la probabilidad de obtener el elemento correcto midiendo el registro.

Nota:

La aplicación conjunta de los pasos 3.b, 3.c y 3.d normalmente se conoce en la documentación como operador de difusión de Grover.

La operación unitaria general aplicada al registro es:

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

Seguimiento del estado del registro paso a paso

Para ilustrar el proceso, vamos a seguir las transformaciones matemáticas del estado del registro para un caso simple en el que solo tenemos dos cúbits y el elemento válido es $\ket{01}.$

1. El registro se inicia en el estado: $$|\text{register}\rangle=|00\rangle$$

2. Después de aplicar $H$ a cada cúbit, el estado del registro se transforma en: $$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$

3. A continuación, se aplica el oráculo de fase para obtener: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$

4. A continuación, H actúa de nuevo sobre cada $cúbit$ para dar: $$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$

5. Ahora el desfase condicional se aplica a todos los estados excepto $\ket{00}$: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$

6. Por último, finalizamos la primera iteración de Grover aplicando $H$ de nuevo para obtener: $$|\text{register}\rangle=\ket{{01}$$

   Siguiendo los pasos anteriores, el elemento válido se encuentra en una sola iteración. Como verá más adelante, esto se debe a que para N=4 y un solo elemento válido, $N_\text{optimal}=1$.

Explicación geométrica

Para ver por qué funciona el algoritmo de Grover, vamos a estudiar el algoritmo desde una perspectiva geométrica. Permita que $\ket{\text{bad}}$ sea la superposición de todos los estados que no son una solución al problema de búsqueda. Si se supone que hay $M$ soluciones válidas:

$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

Definimos el estado $\ket{\text{good}}$ como la superposición de todos los estados que son una solución al problema de búsqueda:

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

Puesto que good y bad son conjuntos mutuamente excluyentes, porque un elemento no puede ser válido y no válido, los estados $\ket{\text{good}}$ y $\ket{\text{bad}}$ son ortogonales. Ambos estados forman la base ortogonal de un plano en el espacio vectorial. Podemos usar este plano para visualizar el algoritmo.

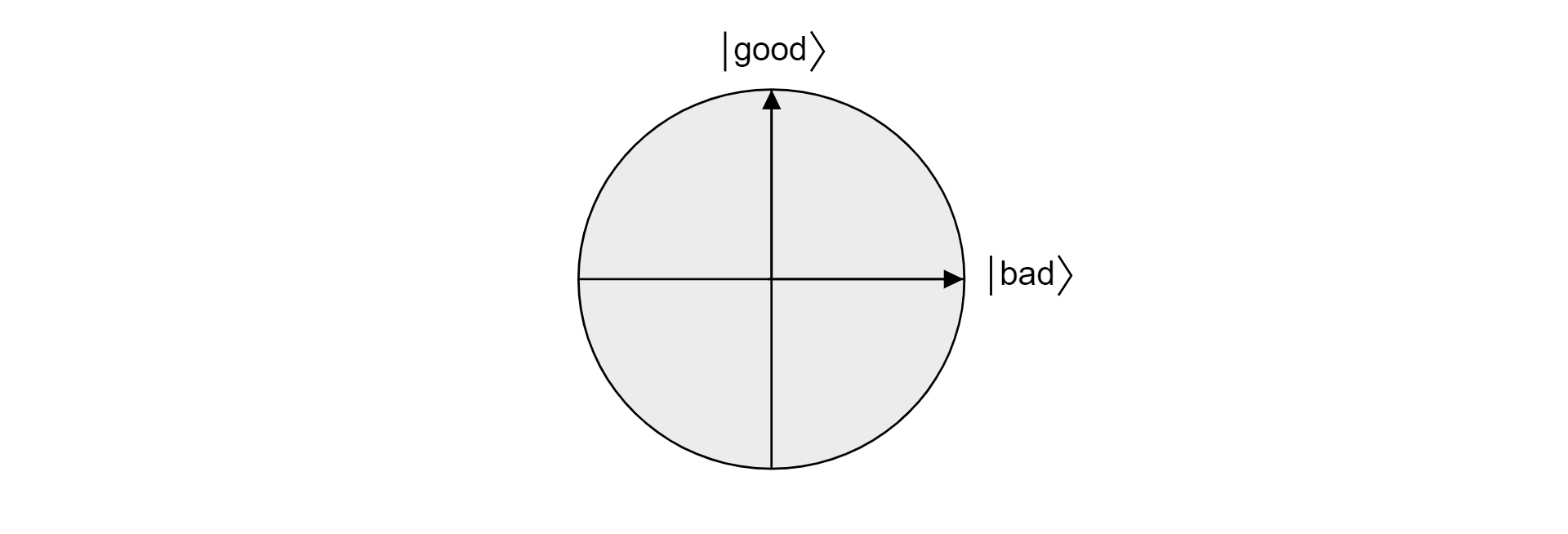
Ahora, supongamos que $\ket{\psi}$ es un estado arbitrario que reside en el plano abarcado por $\ket{\text{good}}$ y $\ket{\text{bad}}$. Cualquier estado que se encuentra en ese plano se puede expresar como:

$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$

donde $\alpha$ y $\beta$ son números reales. Ahora, vamos a presentar el operador de reflexión $R_{\ket{\psi}}$, donde $\ket{\psi}$ es cualquier estado de cúbit que se encuentra en el plano. El operador se define como:

$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$

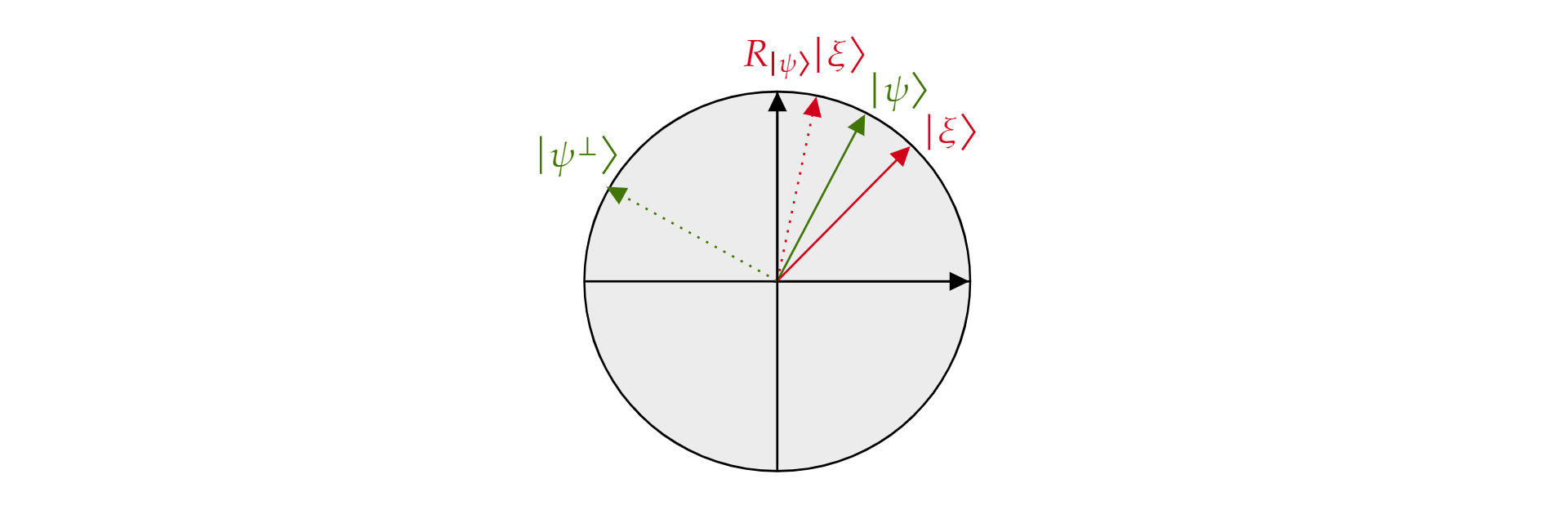
Se denomina operador de reflexión sobre $\ket{\psi}$ porque se puede interpretar geométricamente como reflexión sobre la dirección de $\ket{\psi}$. Para verlo, tome la base ortogonal del plano formado por $\ket{\psi}$ y su complemento ortogonal $\ket{\psi^{\perp}}$. Cualquier estado $\ket{\xi}$ del plano se puede descomponer de esta forma:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Si se aplica el operador $R_{\ket{\psi}}$ a $\ket{\xi}$:

$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

El operador $R_\ket{\psi}$ invierte el componente ortogonal en $\ket{\psi}$, pero deja el componente $\ket{\psi}$ sin cambios. Por lo tanto, $R_\ket{\psi}$ es una reflexión sobre $\ket{\psi}$.

El algoritmo de Grover, después de la primera aplicación de $H$ a cada cúbit, empieza con una superposición uniforme de todos los estados. Esto se puede escribir como:

$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$

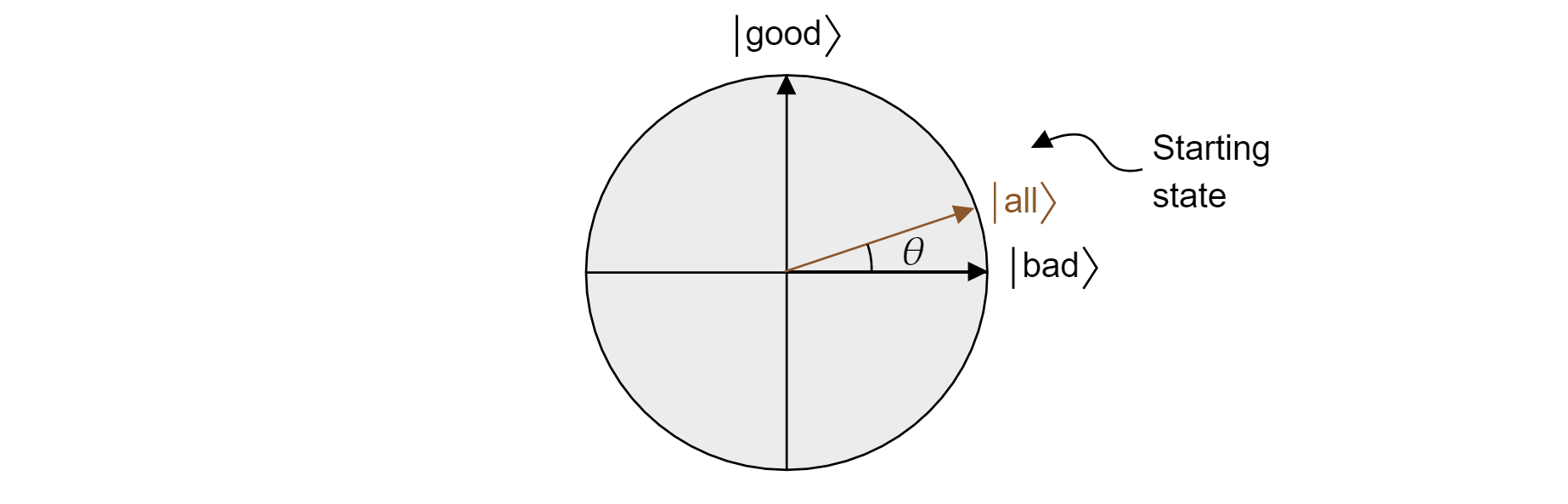
Y, por tanto, el estado reside en el plano. Tenga en cuenta que la probabilidad de obtener un resultado correcto al medir a partir de la superposición igual es simplemente $|\braket{\text{bueno}|{\text{todo}}}|^2=M/N$, que es lo que cabría esperar de una estimación aleatoria.

El oráculo $O_f$ agrega una fase negativa a cualquier solución al problema de búsqueda. Por lo tanto, se puede escribir como una reflexión sobre el eje $\ket{\text{bad}}$:

$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$

Análogamente, el desplazamiento de fase condicional $O_0$ es simplemente una reflexión invertida sobre el estado $\ket{0}$:

$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$

Sabiendo este hecho, es fácil comprobar que la operación de difusión de Grover $-H^{\otimes n} O_0 H^{\otimes n}$ también es una reflexión sobre el estado $\ket{all}$. Simplemente haga lo siguiente:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$

Se ha demostrado que cada iteración del algoritmo de Grover es una composición de dos reflejos $R_\ket{\text{bad}}$ y $R_\ket{\text{all}}$.

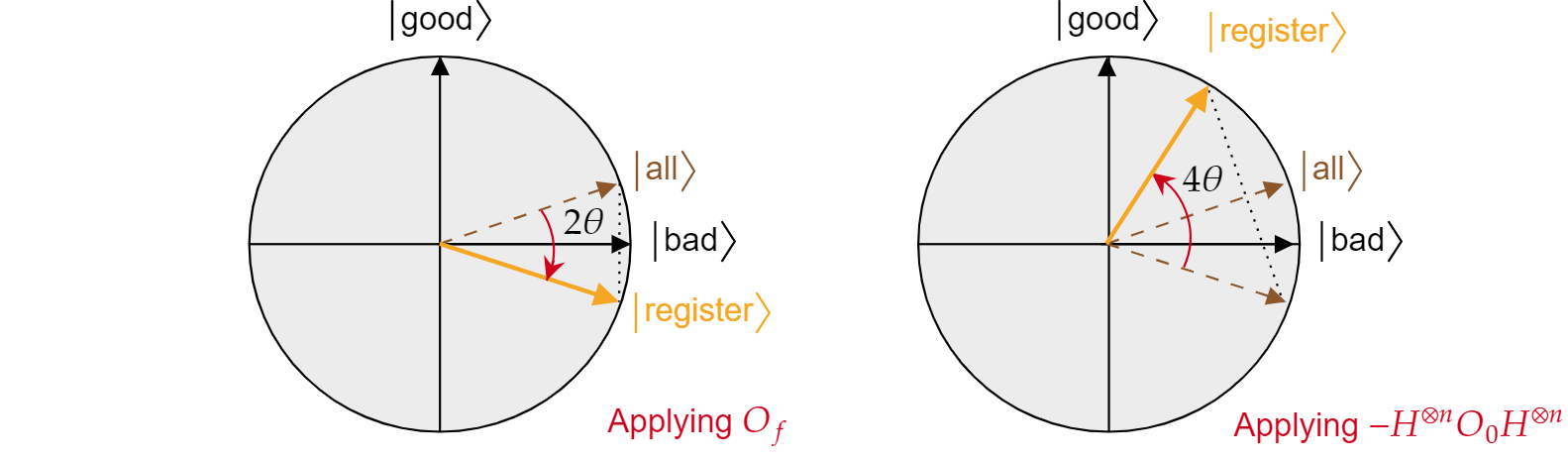
El efecto combinado de cada iteración de Grover es una rotación en sentido contrario a las agujas del reloj de un ángulo $2\theta$. Afortunadamente, el ángulo $\theta$ es fácil de encontrar. Dado que $\theta$ es simplemente el ángulo entre $\ket{\text{all}}$ y $\ket{\text{bad}}$, podemos usar el producto escalar para encontrar el ángulo. Se sabe que $\cos{\theta}=\braket{\text{all}|\text{bad}}$, por lo que necesitamos calcular $\braket{\text{all}|\text{bad}}$. A partir de la descomposición de $\ket{\text{all}}$ en términos de $\ket{\text{bad}}$ y $\ket{\text{good}}$, se obtiene los siguiente:

$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

El ángulo entre el estado del registro y el $\ket{\text{buen}}$ estado disminuye con cada iteración, lo que da lugar a una mayor probabilidad de medir un resultado válido. Para calcular esta probabilidad, solo tiene que calcular $|\braket{\text{un buen}|\text{registro}}|^2$. Indicando el ángulo entre $\ket{\text{good}}$ y $\ket{\text{register}}$$\gamma (k)$, donde $k$ es el recuento de iteraciones:

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

Por lo tanto, la probabilidad de éxito es:

$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

Número óptimo de iteraciones

Como la probabilidad de éxito se puede escribir como una función del número de iteraciones, podemos encontrar el número óptimo de iteraciones $N_{\text{optimal}}$ al calcular el entero positivo más pequeño que (aproximadamente) maximiza la función de probabilidad de éxito.

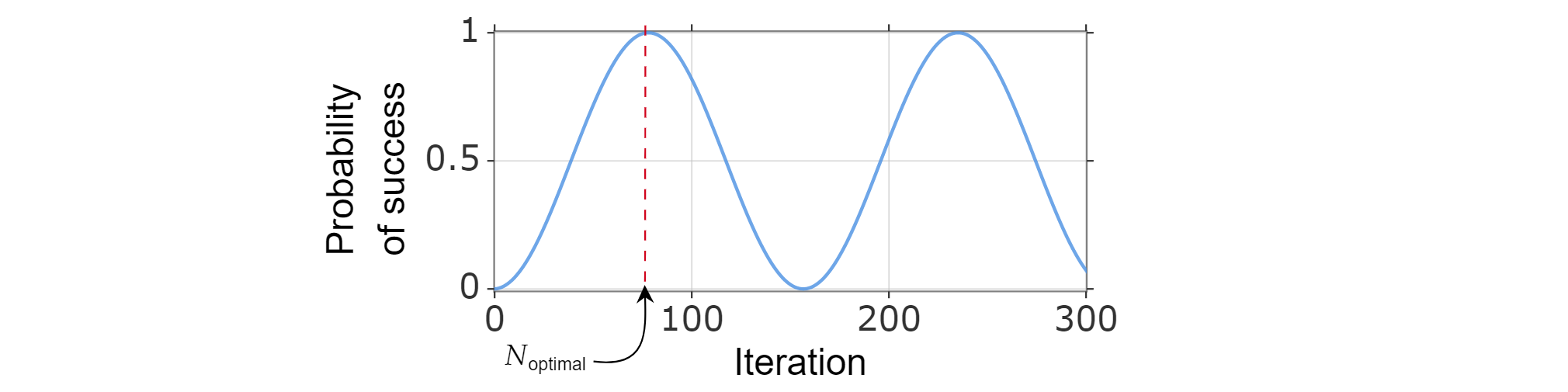
Se sabe que $\sin^2{x}$ alcanza su primer máximo para $x=\frac{\pi}{2}$, por lo que:

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Este es el resultado:

$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$

Donde en el último paso, $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.

Por lo tanto, puede elegir $N_\text{optimal}$ para que sea $N_\text{optimal}\left=\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{2}\right\rfloor$.

Análisis de complejidad

En el análisis anterior, necesitamos $O\left(\sqrt{\frac{N}{M}}\right)$ consultas del oráculo $O_f$ para encontrar un elemento válido. Sin embargo, ¿se puede implementar el algoritmo de forma eficaz en términos de complejidad de tiempo? $O_0$ se basa en la computación de operaciones booleanas en $n$ bits y se sabe que se puede implementar mediante $O(n)$ puertas. También hay dos capas de $n$ puertas Hadamard. Por lo tanto, ambos componentes solo requieren $O(n)$ puertas por iteración. Como $N=2^n$, se deduce que $O(n)=O(log(N))$. Por lo tanto, si necesitamos $O\left(\sqrt{\frac{N}{M}}\right)$ iteraciones y $O(log(N))$ puertas por iteración, la complejidad de tiempo total (sin tener en cuenta la implementación del oráculo) es $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.

La complejidad general del algoritmo depende en última instancia de la complejidad de la implementación del oráculo $O_f$. Si una evaluación de función es mucho más complicada en un equipo cuántico que en uno clásico, el tiempo de ejecución del algoritmo general será más largo en el caso cuántico, aunque técnicamente use menos consultas.

Referencias

Si desea seguir aprendiendo sobre el algoritmo de Grover, puede comprobar cualquiera de los siguientes orígenes:

• Documento original de Lov K. Grover
• Sección algoritmos de búsqueda cuántica de Nielsen, M. A. &Amp; Chuang, I. L. (2010). Quantum Computation and Quantum Information (Computación cuántica e información cuántica).
• Algoritmo de Grover en Arxiv.org

Pasos siguientes

• Representación intermedia cuántica
• Vectores y matrices
• Puertas T y fábricas de T
• Varios qubits