Aplicación de transformaciones en Direct2D

En Dibujo con Direct2D, vimos que el método ID2D1RenderTarget::FillEllipse dibuja una elipse alineada con los ejes x e y. ¿Pero supongamos que desea dibujar una elipse inclinada en un ángulo?

Mediante el uso de transformaciones, puede modificar una forma de las maneras siguientes.

• Rotación alrededor de un punto.
• Ajustar la escala.
• Traducción (desplazamiento en la dirección X o Y).
• Asimetría (también conocida como shear).

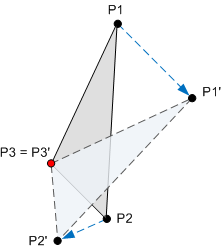
Una transformación es una operación matemática que asigna un conjunto de puntos a un nuevo conjunto de puntos. Por ejemplo, en el diagrama siguiente se muestra un triángulo girado alrededor del punto P3. Una vez aplicada la rotación, el punto P1 se asigna a P1', el punto P2 se asigna a P2' y el punto P3 se asigna a sí mismo.

Las transformaciones se implementan mediante matrices. Sin embargo, no es necesario comprender las matemáticas de las matrices para poder usarlas. Si desea obtener más información sobre las matemáticas, consulte Apéndice: Transformaciones de matriz.

Para aplicar una transformación en Direct2D, llame al método ID2D1RenderTarget::SetTransform . Este método toma una estructura D2D1_MATRIX_3X2_F que define la transformación. Puede inicializar esta estructura llamando a métodos en la clase D2D1::Matrix3x2F . Esta clase contiene métodos estáticos que devuelven una matriz para cada tipo de transformación:

• Matrix3x2F::Rotation
• Matrix3x2F::Scale
• Matrix3x2F::Translation
• Matrix3x2F::Skew

Por ejemplo, el código siguiente aplica una rotación de 20 grados alrededor del punto (100, 100).

pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));

La transformación se aplica a todas las operaciones de dibujo posteriores hasta que vuelva a llamar a SetTransform . Para quitar la transformación actual, llame a SetTransform con la matriz de identidad. Para crear la matriz de identidades, llame a la función Matrix3x2F::Identity .

pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

Dibujar las manos del reloj

Vamos a poner transformaciones para usarlas convirtiendo nuestro programa Circle en un reloj analógico. Podemos hacerlo agregando líneas para las manos.

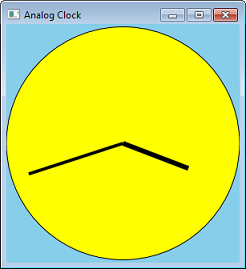
En lugar de calcular las coordenadas de las líneas, podemos calcular el ángulo y, a continuación, aplicar una transformación de rotación. El código siguiente muestra una función que dibuja una mano del reloj. El parámetro fAngle proporciona el ángulo de la mano, en grados.

void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
    m_pRenderTarget->SetTransform(
        D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
            );

    // endPoint defines one end of the hand.
    D2D_POINT_2F endPoint = D2D1::Point2F(
        m_ellipse.point.x,
        m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
        );

    // Draw a line from the center of the ellipse to endPoint.
    m_pRenderTarget->DrawLine(
        m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}

Este código dibuja una línea vertical, comenzando desde el centro de la cara del reloj y finalizando en el punto endPoint. La línea se gira alrededor del centro de la elipse aplicando una transformación de rotación. El punto central de la rotación es el centro de elipse que forma la cara del reloj.

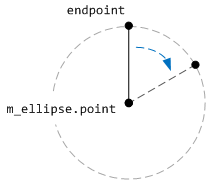
En el código siguiente se muestra cómo se dibuja toda la cara del reloj.

void Scene::RenderScene()
{
    m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));

    m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
    m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);

    // Draw hands
    SYSTEMTIME time;
    GetLocalTime(&time);

    // 60 minutes = 30 degrees, 1 minute = 0.5 degree
    const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
    const float fMinuteAngle =(360.0f / 60) * (time.wMinute);

    DrawClockHand(0.6f,  fHourAngle,   6);
    DrawClockHand(0.85f, fMinuteAngle, 4);

    // Restore the identity transformation.
    m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}

Puede descargar el proyecto completo de Visual Studio desde ejemplo de reloj direct2D. (Sólo para divertirse, la versión de descarga agrega un gradiant radial a la cara del reloj).

Combinación de transformaciones

Las cuatro transformaciones básicas se pueden combinar multiplicando dos o más matrices. Por ejemplo, el código siguiente combina una rotación con una traducción.

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);

pRenderTarget->SetTransform(rot * trans);

La clase Matrix3x2F proporciona operator*() para la multiplicación de matrices. El orden en que se multiplican las matrices es importante. Establecer una transformación (M × N) significa "Aplicar M primero, seguido de N". Por ejemplo, esta es la rotación seguida de la traducción:

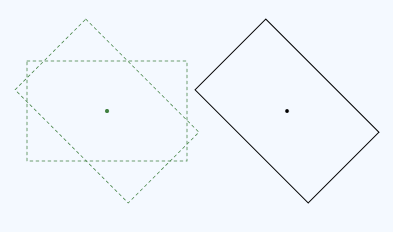
Este es el código de esta transformación:

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);

Ahora compare esa transformación con una transformación en orden inverso, la traducción seguida de la rotación.

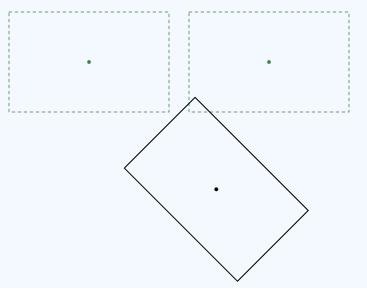
La rotación se realiza alrededor del centro del rectángulo original. Este es el código de esta transformación.

D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);

Como puede ver, las matrices son las mismas, pero el orden de las operaciones ha cambiado. Esto sucede porque la multiplicación de matriz no es conmutativa: M × N ≠ N × M.

Siguientes

Apéndice: Transformaciones de matriz