Notes
L’accès à cette page nécessite une autorisation. Vous pouvez essayer de vous connecter ou de modifier des répertoires.
L’accès à cette page nécessite une autorisation. Vous pouvez essayer de modifier des répertoires.
Vous pouvez considérer la transformation de projection comme le contrôle des internes de la caméra ; il est analogue au choix d’un objectif pour l’appareil photo. Il s’agit du plus compliqué des trois types de transformation. Cette discussion sur la transformation de projection est organisée dans les rubriques suivantes.
La matrice de projection est généralement une projection d’échelle et de perspective. La transformation de projection convertit le frustum d’affichage en forme cuboïde. Étant donné que la fin proche du frustum d’affichage est plus petite que l’extrémité éloignée, cela a l’effet de développer des objets proches de la caméra ; c’est ainsi que la perspective est appliquée à la scène.
Dans le frustum d’affichage, la distance entre l’appareil photo et l’origine de l’espace de transformation d’affichage est définie arbitrairement comme D, de sorte que la matrice de projection ressemble à l’illustration suivante.
illustration 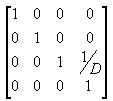
La matrice d’affichage traduit l’appareil photo à l’origine en traduire dans la direction z par - D. La matrice de traduction est semblable à l’illustration suivante.
illustration 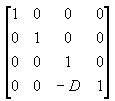
La multiplication de la matrice de traduction par la matrice de projection (T*P) donne la matrice de projection composite, comme illustré dans l’illustration suivante.
illustration 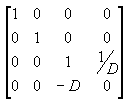
La transformation de perspective convertit un frustum d’affichage en un nouvel espace de coordonnées. Notez que le frustum devient cuboïde et que l’origine passe du coin supérieur droit de la scène au centre, comme illustré dans le diagramme suivant.
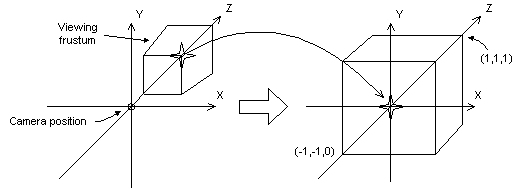
Dans la transformation de perspective, les limites des directions x et y sont -1 et 1. Les limites de la direction z sont 0 pour le plan avant et 1 pour le plan arrière.
Cette matrice traduit et met à l’échelle des objets basés sur une distance spécifiée entre l’appareil photo et le plan de découpage proche, mais il ne considère pas le champ de vue (fov), et les valeurs z qu’elle produit pour les objets de la distance peuvent être presque identiques, ce qui rend les comparaisons de profondeur difficiles. La matrice suivante traite ces problèmes et ajuste les sommets pour tenir compte des proportions de la fenêtre d’affichage, ce qui en fait un bon choix pour la projection de perspective.
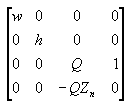
Dans cette matrice, Zn est la valeur z du plan de découpage proche. Les variables w, h et Q ont les significations suivantes. Notez que fovw et fovk représentent les champs horizontaux et verticaux de la vue, en radians.
équations 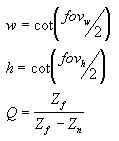
Pour votre application, l’utilisation d’angles de vue de champ pour définir les coefficients de mise à l’échelle x et y peut ne pas être aussi pratique que l’utilisation des dimensions horizontales et verticales de la fenêtre d’affichage (dans l’espace de caméra). À mesure que les mathématiques fonctionnent, les deux équations suivantes pour w et h utilisent les dimensions de la fenêtre d’affichage et sont équivalentes aux équations précédentes.
équations 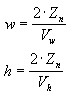
Dans ces formules, Zn représente la position du plan de découpage proche, et les variables Vw et Vh représentent la largeur et la hauteur de la fenêtre d’affichage, dans l’espace de caméra.
Pour une application C++, ces deux dimensions correspondent directement aux membres Width et Height de la structure D3DVIEWPORT9.
Quelle que soit la formule que vous décidez d’utiliser, veillez à définir Zn sur une valeur aussi importante que possible, car les valeurs z extrêmement proches de la caméra ne varient pas beaucoup. Cela rend les comparaisons de profondeur à l’aide de mémoires tampons z 16 bits quelque peu compliquées.
Comme avec les transformations mondiales et d’affichage, vous appelez la méthode IDirect3DDevice9 ::SetTransform pour définir la transformation de projection.
Configuration d’une matrice de projection
L’exemple de fonction ProjectionMatrix suivant définit les plans de découpage avant et arrière, ainsi que le champ horizontal et vertical des angles de vue. Les champs de vue doivent être inférieurs à pi radians.
D3DXMATRIX
ProjectionMatrix(const float near_plane, // Distance to near clipping
// plane
const float far_plane, // Distance to far clipping
// plane
const float fov_horiz, // Horizontal field of view
// angle, in radians
const float fov_vert) // Vertical field of view
// angle, in radians
{
float h, w, Q;
w = (float)1/tan(fov_horiz*0.5); // 1/tan(x) == cot(x)
h = (float)1/tan(fov_vert*0.5); // 1/tan(x) == cot(x)
Q = far_plane/(far_plane - near_plane);
D3DXMATRIX ret;
ZeroMemory(&ret, sizeof(ret));
ret(0, 0) = w;
ret(1, 1) = h;
ret(2, 2) = Q;
ret(3, 2) = -Q*near_plane;
ret(2, 3) = 1;
return ret;
} // End of ProjectionMatrix
Après avoir créé la matrice, définissez-la avec IDirect3DDevice9 ::SetTransform en spécifiant D3DTS_PROJECTION.
La bibliothèque utilitaire D3DX fournit les fonctions suivantes pour vous aider à configurer votre matrice de projection.
- D3DXMatrixPerspectiveLH
- D3DXMatrixPerspectiveRH
- D3DXMatrixPerspectiveFovLH
- D3DXMatrixPerspectiveFovRH
- D3DXMatrixPerspectiveOffCenterLH
- D3DXMatrixPerspectiveOffCenterRH
Matrice de projection conviviale W
Direct3D peut utiliser le composant w d’un vertex qui a été transformé par le monde, les vues et les matrices de projection pour effectuer des calculs basés sur la profondeur dans la mémoire tampon de profondeur ou les effets de brouillard. Les calculs tels que ceux-ci nécessitent que votre matrice de projection normalise w pour être équivalente à l’espace mondial z. En bref, si votre matrice de projection comprend un coefficient (3,4) qui n’est pas 1, vous devez mettre à l’échelle tous les coefficients en fonction de l’inverse du coefficient (3,4) pour créer une matrice appropriée. Si vous ne fournissez pas de matrice conforme, les effets de brouillard et la mise en mémoire tampon de profondeur ne sont pas appliqués correctement.
L’illustration suivante montre une matrice de projection non conforme et la même matrice mise à l’échelle afin que le brouillard relatif aux yeux soit activé.

Dans les matrices précédentes, toutes les variables sont supposées être différente de zéro. Pour plus d’informations sur le brouillard relatif aux yeux, consultez Eye-Relative et la profondeur basée sur Z. Pour plus d’informations sur la mise en mémoire tampon de profondeur basée sur w, consultez tampons de profondeur (Direct3D 9).
Direct3D utilise la matrice de projection actuellement définie dans ses calculs de profondeur basés sur w. Par conséquent, les applications doivent définir une matrice de projection conforme pour recevoir les fonctionnalités w souhaitées, même si elles n’utilisent pas Direct3D pour les transformations.
Rubriques connexes