Útmutató: Mátrix-szorzás

Ez a részletes útmutató bemutatja, hogyan használható a C++ AMP a mátrix-szorzás végrehajtásának felgyorsítására. Két algoritmust mutatunk be, egyet burkolás nélkül, egyet pedig burkolással.

Előfeltételek

Kezdés előtt:

• Olvassa el a C++ AMP áttekintését.
• Olvasd el a Csempék használata.
• Győződjön meg arról, hogy legalább Windows 7 vagy Windows Server 2008 R2 rendszert futtat.

Megjegyzés:

A C++ AMP fejlécek elavultak a Visual Studio 2022 17.0-s verziójától kezdve. Az AMP-fejlécek beépítése építési hibákat fog okozni. A figyelmeztetések elnémításához a _SILENCE_AMP_DEPRECATION_WARNINGS definiálása előtt az AMP-fejléceket be kell vonni.

A projekt létrehozása

Az új projekt létrehozására vonatkozó utasítások a Visual Studio telepített verziójától függően eltérőek lehetnek. A Visual Studio előnyben részesített verziójának dokumentációját a Verzió választóvezérlő használatával tekintheti meg. A lap tartalomjegyzékének tetején található.

A projekt létrehozása a Visual Studióban

1. A menüsávOn válassza azÚj>projekt> lehetőséget az Új projekt létrehozása párbeszédpanel megnyitásához.

2. A párbeszédpanel tetején állítsa a Nyelvbeállítást C++-ra, állítsa a PlatformotWindowsra, és állítsa a Projekt típusátkonzolra.

3. A projekttípusok szűrt listájában válassza az Üres projekt lehetőséget, majd a Tovább elemet. A következő lapon írja be a MatrixMultiply kifejezést a Név mezőbe a projekt nevének megadásához, és szükség esetén adja meg a projekt helyét.

   

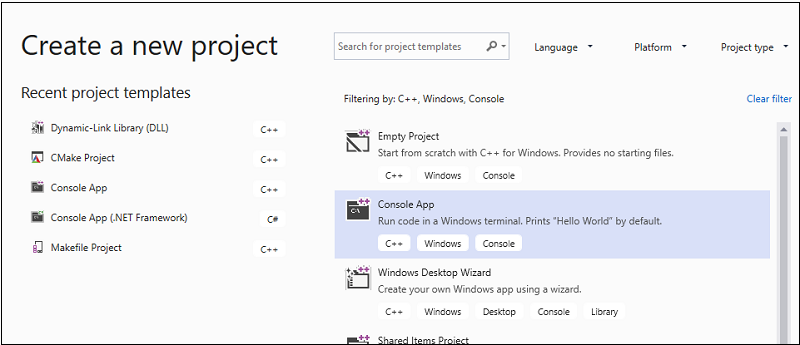
4. Válassza a Létrehozás gombot az ügyfélprojekt létrehozásához.

5. A Megoldáskezelőben nyissa meg a forrásfájlok helyi menüjét, majd válassza azÚj elem>.

6. Az Új elem hozzáadása párbeszédpanelen válassza a C++ fájl (.cpp) lehetőséget, írja be a MatrixMultiply.cpp a Név mezőbe, majd válassza a Hozzáadás gombot.

Szorzás burkolás nélkül

Ebben a szakaszban tekintsük át két mátrix, az A és a B szorzását, amelyek a következőképpen vannak definiálva:

Az A egy 3-by-2 mátrix, a B pedig 2-by-3 mátrix. Az A és B szorzata a következő 3x3-as mátrix. A szorzat kiszámítása az A sorainak és a B elem oszlopainak elemenkénti szorzatával történik.

Szorzás C++ AMP használata nélkül

1. Nyissa meg MatrixMultiply.cpp, és a következő kóddal cserélje le a meglévő kódot.

   #include <iostream>
   
   void MultiplyWithOutAMP() {
       int aMatrix[3][2] = {{1, 4}, {2, 5}, {3, 6}};
       int bMatrix[2][3] = {{7, 8, 9}, {10, 11, 12}};
       int product[3][3] = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}};
   
       for (int row = 0; row < 3; row++) {
           for (int col = 0; col < 3; col++) {
               // Multiply the row of A by the column of B to get the row, column of product.
               for (int inner = 0; inner < 2; inner++) {
                   product[row][col] += aMatrix[row][inner] * bMatrix[inner][col];
               }
               std::cout << product[row][col] << "  ";
           }
           std::cout << "\n";
       }
   }
   
   int main() {
       MultiplyWithOutAMP();
       getchar();
   }
   

   Az algoritmus a mátrix-szorzás definíciójának egyszerű implementálása. Nem használ párhuzamos vagy menetes algoritmusokat a számítási idő csökkentéséhez.

2. A menüsávon válassza az Összes fájl>mentése lehetőséget.

3. A hibakeresés megkezdéséhez és a kimenet helyességének ellenőrzéséhez válassza az F5 billentyűparancsot.

4. Az Enter elemet választva lépjen ki az alkalmazásból.

C++ AMP használatával való szorzás

1. A MatrixMultiply.cpp adja hozzá a következő kódot a main metódus előtt.

   void MultiplyWithAMP() {
   int aMatrix[] = { 1, 4, 2, 5, 3, 6 };
   int bMatrix[] = { 7, 8, 9, 10, 11, 12 };
   int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 };
   
   array_view<int, 2> a(3, 2, aMatrix);
   
   array_view<int, 2> b(2, 3, bMatrix);
   
   array_view<int, 2> product(3, 3, productMatrix);
   
   parallel_for_each(product.extent,
      [=] (index<2> idx) restrict(amp) {
          int row = idx[0];
          int col = idx[1];
          for (int inner = 0; inner <2; inner++) {
              product[idx] += a(row, inner)* b(inner, col);
          }
      });
   
   product.synchronize();
   
   for (int row = 0; row <3; row++) {
      for (int col = 0; col <3; col++) {
          //std::cout << productMatrix[row*3 + col] << "  ";
          std::cout << product(row, col) << "  ";
      }
      std::cout << "\n";
     }
   }
   

   Az AMP-kód hasonlít a nem AMP-kódra. A parallel_for_each hívás elindít egy szálat az product.extent minden eleméhez, és helyettesíti a for ciklusokat a sorok és oszlopok esetében. A sorban és oszlopban lévő cella értéke a következőben idxérhető el: . Az objektum elemeit array_view az operátor és az [] indexváltozó, illetve az () operátor, valamint a sor- és oszlopváltozók használatával érheti el. A példa mindkét módszert szemlélteti. A array_view::synchronize metódus a változó értékeit product visszamásolja a productMatrix változóba.

2. Adja hozzá a következő include és using utasításokat a MatrixMultiply.cpp tetejére.

   #include <amp.h>
   using namespace concurrency;
   

3. Módosítsa a main metódust úgy, hogy meghívja a MultiplyWithAMP metódust.

   int main() {
       MultiplyWithOutAMP();
       MultiplyWithAMP();
       getchar();
   }
   

4. A Hibakeresésmegkezdéséhez és a kimenet helyességének ellenőrzéséhez nyomja le a Ctrl +F5 billentyűparancsot.

5. Nyomja le a szóközbillentyűt az alkalmazásból való kilépéshez.

Szorzás a burkolással

A burkolás egy olyan technika, amelyben az adatokat egyenlő méretű részhalmazokra, azaz csempékre particionálhatja. Három dolog változik a burkolás használatakor.

• tile_static Létrehozhat változókat. A térben lévő tile_static adatokhoz való hozzáférés sokszor gyorsabb lehet, mint a globális térben lévő adatokhoz való hozzáférés. Minden csempéhez létrejön egy változópéldány tile_static , és a csempe összes szála hozzáfér a változóhoz. A burkolás elsődleges előnye a tile_static hozzáférés által elért teljesítménynövekedés.

• Meghívhatja a tile_barrier::wait metódust, hogy egy csempe összes szálát leállítsák egy megadott kódsoron. Nem garantálhatja a szálak futtatásának sorrendjét, csak azt, hogy egy csempén lévő összes szál le fog állni a tile_barrier::wait hívásnál, mielőtt folytatják a végrehajtást.

• Hozzáféréssel rendelkezik a szál indexéhez a teljes array_view objektumhoz képest, valamint a csempére vonatkozó indexhez. A helyi index használatával egyszerűbbé teheti a kód olvasását és hibakeresését.

A mátrixok szorzásának előnyeinek kihasználásához az algoritmusnak csempékre kell particionálja a mátrixot, majd a csempeadatokat változókba tile_static kell másolnia a gyorsabb hozzáférés érdekében. Ebben a példában a mátrix egyenlő méretű részösszegekre van particionálva. A szorzat a részmátrixok szorzásával nyerhető. A példában szereplő két mátrix és termékük a következők:

A mátrixok négy 2x2 mátrixra vannak particionálva, amelyek a következőképpen vannak definiálva:

Az A és a B terméke mostantól az alábbiak szerint írható és számítható ki:

Mivel a mátrixok ah 2x2 mátrixok, az összes termék és összegük is 2x2 mátrix. Ebből az is következik, hogy az A és a B szorzata a vártnak megfelelően 4x4 mátrix. Az algoritmus gyors ellenőrzéséhez számítsa ki az elem értékét a termék első sorában, első oszlopában. A példában ez a sor első sorában és első oszlopában ae + bglévő elem értéke lenne. Csak az egyes kifejezésekhez tartozó ae és bg első oszlopát és első sorát kell kiszámítania. Ennek az értéke ae az (1 * 1) + (2 * 5) = 11. Az bg értéke (3 * 1) + (4 * 5) = 23. A végső érték a 11 + 23 = 34helyes érték.

Az algoritmus implementálásához a kód:

• A tiled_extent objektumot használ a extent hívásban egy parallel_for_each objektum helyett.

• A tiled_index objektumot használ a index hívásban egy parallel_for_each objektum helyett.

• Változókat hoz létre tile_static az al-mátrixok tárolásához.

• A tile_barrier::wait módszer leállítja a szálakat az al-mátrixok szorzatának kiszámítási folyamatában.

Szorzás az AMP és a csempézés használatával

1. A MatrixMultiply.cpp adja hozzá a következő kódot a main metódus előtt.

   void MultiplyWithTiling() {
       // The tile size is 2.
       static const int TS = 2;
   
       // The raw data.
       int aMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 };
       int bMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 };
       int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
   
       // Create the array_view objects.
       array_view<int, 2> a(4, 4, aMatrix);
       array_view<int, 2> b(4, 4, bMatrix);
       array_view<int, 2> product(4, 4, productMatrix);
   
       // Call parallel_for_each by using 2x2 tiles.
       parallel_for_each(product.extent.tile<TS, TS>(),
           [=] (tiled_index<TS, TS> t_idx) restrict(amp)
           {
               // Get the location of the thread relative to the tile (row, col)
               // and the entire array_view (rowGlobal, colGlobal).
               int row = t_idx.local[0];
               int col = t_idx.local[1];
               int rowGlobal = t_idx.global[0];
               int colGlobal = t_idx.global[1];
               int sum = 0;
   
               // Given a 4x4 matrix and a 2x2 tile size, this loop executes twice for each thread.
               // For the first tile and the first loop, it copies a into locA and e into locB.
               // For the first tile and the second loop, it copies b into locA and g into locB.
               for (int i = 0; i < 4; i += TS) {
                   tile_static int locA[TS][TS];
                   tile_static int locB[TS][TS];
                   locA[row][col] = a(rowGlobal, col + i);
                   locB[row][col] = b(row + i, colGlobal);
                   // The threads in the tile all wait here until locA and locB are filled.
                   t_idx.barrier.wait();
   
                   // Return the product for the thread. The sum is retained across
                   // both iterations of the loop, in effect adding the two products
                   // together, for example, a*e.
                   for (int k = 0; k < TS; k++) {
                       sum += locA[row][k] * locB[k][col];
                   }
   
                   // All threads must wait until the sums are calculated. If any threads
                   // moved ahead, the values in locA and locB would change.
                   t_idx.barrier.wait();
                   // Now go on to the next iteration of the loop.
               }
   
               // After both iterations of the loop, copy the sum to the product variable by using the global location.
               product[t_idx.global] = sum;
           });
   
       // Copy the contents of product back to the productMatrix variable.
       product.synchronize();
   
       for (int row = 0; row <4; row++) {
           for (int col = 0; col <4; col++) {
               // The results are available from both the product and productMatrix variables.
               //std::cout << productMatrix[row*3 + col] << "  ";
               std::cout << product(row, col) << "  ";
           }
           std::cout << "\n";
       }
   }
   

   Ez a példa jelentősen különbözik a csempézés nélküli példától. A kód az alábbi fogalmi lépéseket használja:

   1. Másolja a csempék[0,0] elemeit a a fájlba locA. Másolja a csempék[0,0] elemeit a b fájlba locB. Figyeljen arra, hogy a product van csempézve, nem pedig a a és a b. Ezért globális indexeket használ a a, b és a product eléréséhez. A tile_barrier::wait hívás elengedhetetlen. Mindaddig leállítja az összes szálat a csempén, amíg mind a locA, mind a locB meg nem töltődik.

   2. Szorozzuk meg a locA-t locB-gyel, és helyezze el az eredményeket product.

   3. Másolja a tile[0,1] elemet a a-ból a locA-ba. Másolja a(z) [1,0] csempe elemeit a b fájlba locB.

   4. Szorozza meg locA és locB elemeit, majd adja hozzá azokat a product-ben már meglévő eredményekhez.

   5. A csempe[0,0] szorzása befejeződött.

   6. Ismételje meg a műveletet a másik négy csempén. Nincs külön indexelés a csempékre, és a szálak tetszőleges sorrendben hajthatók végre. Az egyes szálak végrehajtásakor a tile_static változók megfelelően jönnek létre az egyes csempékhez, és a tile_barrier::wait vezérli a program folyamatát.

   7. Az algoritmus alapos vizsgálata során figyelje meg, hogy az egyes almátrixok kétszer töltődnek be egy tile_static memóriába. Az adatátvitel időt vesz igénybe. Ha azonban az adatok a memóriában tile_static lesznek, az adatokhoz való hozzáférés sokkal gyorsabb. Mivel a termékek kiszámításához ismételt hozzáférésre van szükség az alanyagok értékeihez, a teljesítmény általánosan megnő. Minden algoritmushoz kísérletezni kell az optimális algoritmus és csempeméret megtalálásához.

   A nem AMP- és nem csempés példák esetén az A és B összes eleme négyszer érhető el a globális memóriából a szorzat kiszámításához. A csempepéldában minden elem kétszer lesz elérhető a globális memóriából, négyszer pedig a tile_static memóriából. Ez nem jelentős teljesítménynövekedés. Ha azonban az A és a B 1024x1024 mátrix lenne, és a csempe mérete 16 lenne, jelentős teljesítménynövekedés lenne. Ebben az esetben minden elem csak 16 alkalommal lesz a memóriába tile_static másolva, és 1024-szer lesz elérhető a memóriából tile_static .

2. Módosítsa a fő metódust úgy, hogy meghívja az MultiplyWithTiling metódust, ahogyan az látható.

   int main() {
       MultiplyWithOutAMP();
       MultiplyWithAMP();
       MultiplyWithTiling();
       getchar();
   }
   

3. A Hibakeresésmegkezdéséhez és a kimenet helyességének ellenőrzéséhez nyomja le a Ctrl +F5 billentyűparancsot.

4. Nyomja le a Szóköz billentyűt az alkalmazásból való kilépéshez.

Lásd még

C++ AMP (C++ gyorsított masszív párhuzamosság)
Útmutató: C++ AMP-alkalmazás hibakeresése