Teoria dell'algoritmo di ricerca di Grover

Questo articolo contiene una spiegazione teorica dettagliata dei principi matematici alla base dell'algoritmo di Grover.

Per un'implementazione pratica dell'algoritmo di Grover per risolvere i problemi matematici, vedere Implementare l'algoritmo di ricerca di Grover.

Dichiarazione del problema

Qualsiasi attività di ricerca può essere espressa con una funzione astratta $f(x)$ che accetta elementi di ricerca $x$. Se l'elemento $x$ è una soluzione per l'attività di ricerca, allora $f(x)=1$. Se l'elemento $x$ non è una soluzione, allora $f(x)=0$. Il problema di ricerca consiste nel trovare qualsiasi elemento $x_0$ tale che $f(x_0)=1$.

L'attività che l'algoritmo di Grover intende risolvere può essere espressa come segue: data una funzione classica $f(x):\{0,1\}^n \rightarrow\{0,1\}$, dove $n$ è la dimensione in bit dello spazio di ricerca, trovare un $x_0$ di input per cui $f(x_0)=1$. La complessità dell'algoritmo viene misurata in base al numero di usi della funzione $f(x)$. In genere, nello scenario peggiore, $f(x)$ deve essere valutato un totale di $N-1$ volte, dove $N=2^n$, provando tutte le possibilità. Dopo $N-1$ elementi, deve essere l'ultimo elemento. L'algoritmo quantistico di Grover può risolvere questo problema molto più velocemente, offrendo una velocità quadratica. Quadratico significa in questo caso che sarebbero necessarie solo $\sqrt{N}$ valutazioni, rispetto a $N$.

Struttura dell'algoritmo

Si supponga che siano presenti $N=2^n$ elementi idonei per l'attività di ricerca e che siano indicizzati assegnando a ogni elemento un numero intero compreso tra $0$ e $N-1$. Si supponga inoltre che siano presenti $M$ input validi diversi, a indicare che sono presenti $M$ input per i quali $f(x)=1$. I passaggi dell'algoritmo sono quindi i seguenti:

1. Iniziare con un registro di $n$ qubit inizializzati nello stato $\ket{0}$.
2. Preparare il registro in una sovrapposizione uniforme applicando $H$ a ogni qubit del registro: $$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
3. Applicare le operazioni seguenti al registro $N_{\text{optimal}}$ volte:
   1. L'oracolo della fase $O_f$ che applica uno spostamento di fase condizionale di $-1$ per gli elementi della soluzione.
   2. Applicare $H$ a ogni qubit nel registro.
   3. Uno spostamento di fase condizionale di $-1$ a ogni stato di base computazionale ad eccezione di $\ket{0}$. Può essere rappresentato dall'operazione unitaria $-O_0$, in quanto $O_0$ rappresenta solo lo spostamento della fase condizionale a $\ket{0}$.
   4. Applicare $H$ a ogni qubit nel registro.
4. Misurare il registro per ottenere l'indice di un elemento che è una soluzione con probabilità molto elevata.
5. Controllare se si tratta di una soluzione valida. In caso contrario, ricominciare.

$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ è il numero ottimale di iterazioni che ottimizza la probabilità di ottenere l'elemento corretto misurando il registro.

Nota

L'applicazione congiunta dei passaggi 3.b, 3.c e 3.d è in genere nota nella documentazione come operatore di diffusione di Grover.

L'operazione unitaria complessiva applicata al registro è:

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

Stato dettagliato del registro passo-passo

Per illustrare il processo, di seguito si seguiranno le trasformazioni matematiche dello stato del registro per un caso semplice in cui sono presenti solo due qubit e l'elemento valido è $\ket{01}.$

1. Lo stato iniziale del registro è $$|\text{register}\rangle=|00\rangle$$

2. Dopo aver applicato $H$ a ogni qubit, lo stato del registro si trasforma in: $$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$

3. Viene quindi applicato l'oracolo di fase per ottenere: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$

4. $H$ agisce quindi di nuovo su ogni qubit per fornire: $$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$

5. Lo spostamento di fase condizionale viene ora applicato a ogni stato ad eccezione di $\ket{00}$: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$

6. Infine, la prima iterazione di Grover termina applicando di nuovo $H$ per ottenere: $$|\text{register}\rangle=\ket{{01}$$

   Seguendo i passaggi precedenti, l'elemento valido viene trovato in una singola iterazione. Come si vedrà più avanti, questo è perché per N=4 e un singolo elemento valido, $N_\text{optimal}=1$.

Spiegazione geometrica

Per capire perché funziona l'algoritmo di Grover, vale la pena di esaminare l'algoritmo da una prospettiva geometrica. Si supponga che lo stato $\ket{\text{bad}}$ sia la sovrapposizione di tutti gli stati che non sono una soluzione al problema di ricerca. Supponendo che siano presenti $M$ soluzioni valide:

$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

Lo stato $\ket{\text{good}}$ viene definito come la sovrapposizione di tutti gli stati che sono una soluzione al problema di ricerca:

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

Dato che i set good e bad si escludono a vicenda perché un elemento non può essere valido e non valido, gli stati $\ket{\text{good}}$ e $\ket{\text{bad}}$ sono ortogonali. Entrambi gli stati formano la base ortogonale di un piano nello spazio vettoriale. È possibile usare questo piano per visualizzare l'algoritmo.

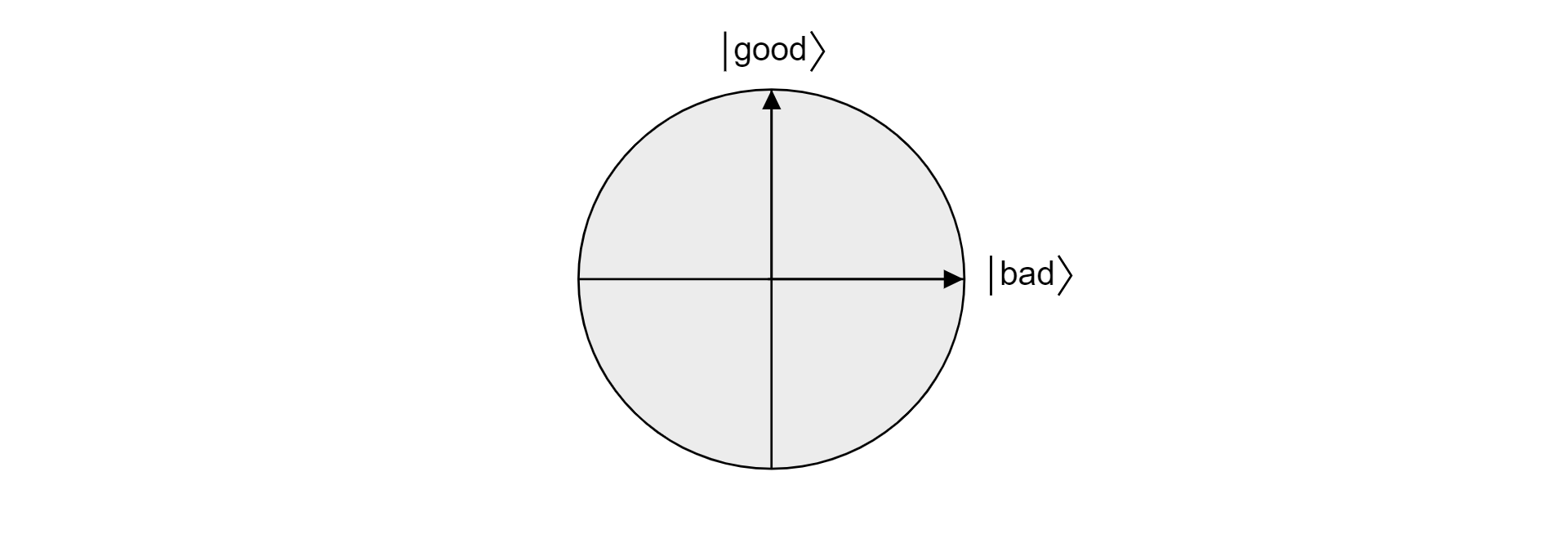
Si supponga ora che $\ket{\psi}$ sia uno stato arbitrario che si trova nel piano che si estende tra $\ket{\text{good}}$ e $\ket{\text{bad}}$. Qualsiasi stato in tale piano può essere espresso come:

$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$

dove $\alpha$ e $\beta$ sono numeri reali. A questo punto, è opportuno introdurre l'operatore di reflection $R_{\ket{\psi}}$, dove $\ket{\psi}$ è qualsiasi stato di qubit che si trova nel piano. L'operatore è definito come segue:

$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$

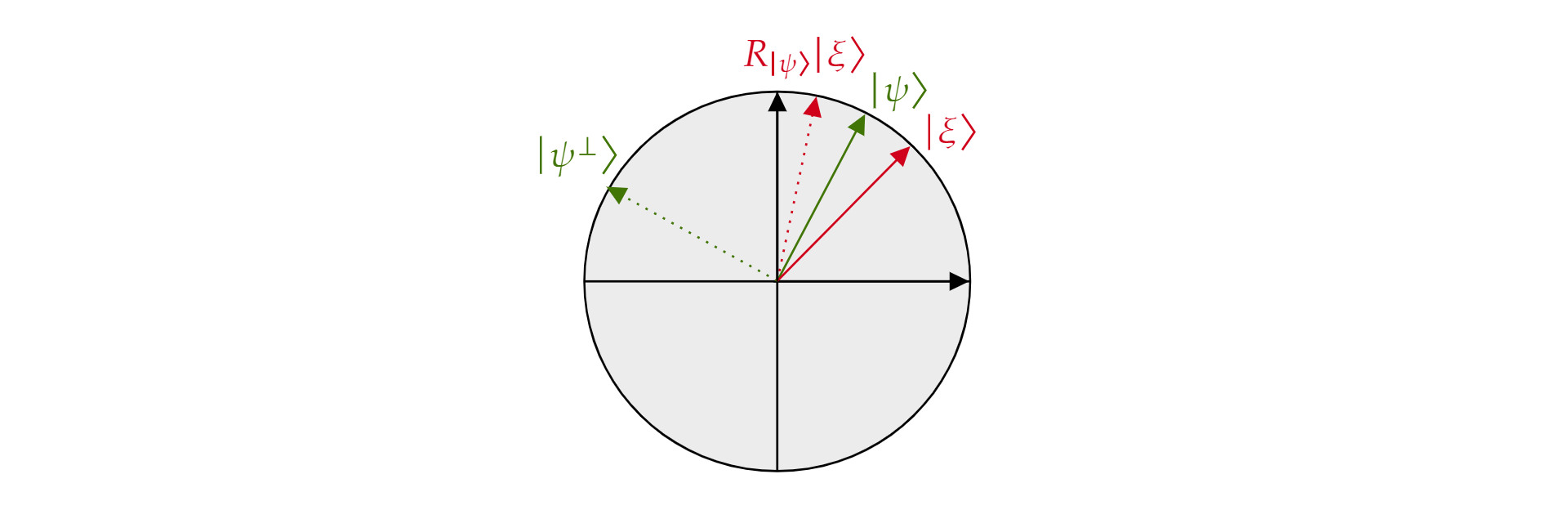
Viene chiamato operatore di reflection per $\ket{\psi}$ perché può essere interpretato geometricamente come reflection per la direzione di $\ket{\psi}$. Per visualizzarlo, prendere la base ortogonale del piano formato da $\ket{\psi}$ e il relativo complemento ortogonale $\ket{\psi^{\perp}}$. Qualsiasi stato $\ket{\xi}$ del piano può essere scomposto in questo modo:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Se si applica l'operatore $R_{\ket{\psi}}$ a $\ket{\xi}$:

$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

L'operatore $R_\ket{\psi}$ inverte il componente ortogonale in $\ket{\psi}$, ma lascia invariato il componente $\ket{\psi}$. Pertanto, $R_\ket{\psi}$ è una reflection per $\ket{\psi}$.

L'algoritmo di Grover, dopo la prima applicazione di $H$ a ogni qubit, inizia con una sovrapposizione uniforme di tutti gli stati. Questa operazione può essere scritta come segue:

$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$

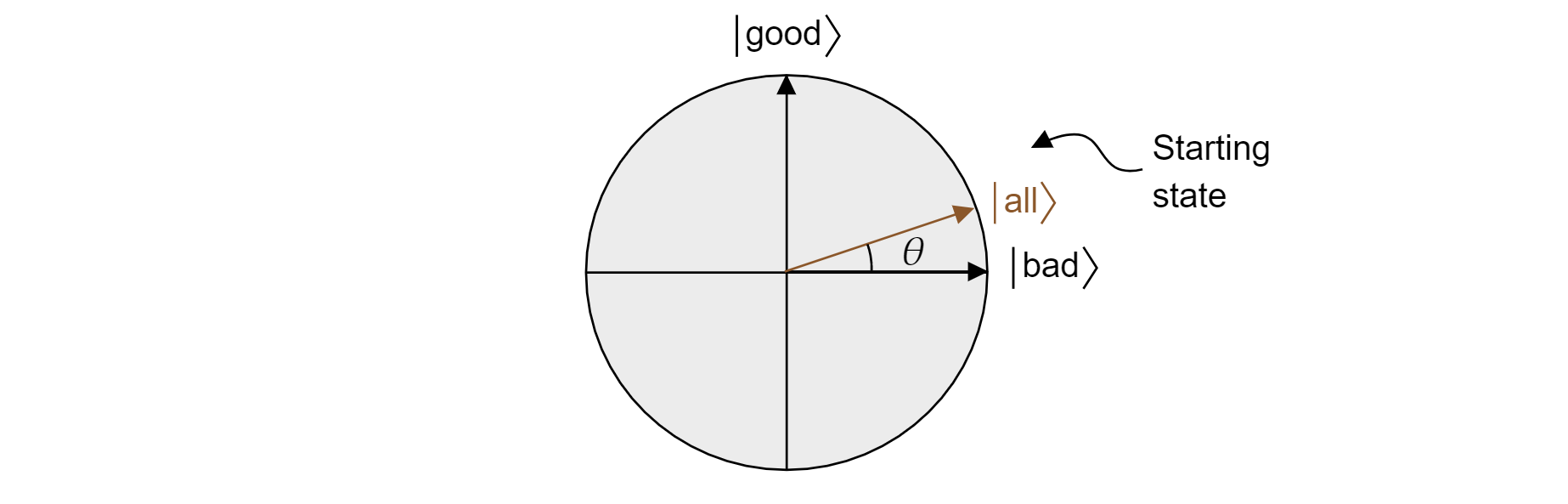
E quindi lo stato risiede nel piano. Si noti che la probabilità di ottenere un risultato corretto quando si misura dalla sovrapposizione uguale è sufficiente $|\braket{\text{}|{\text{tutto^}}}|2=M/N$, che è quello che si prevede da un'ipotesi casuale.

L'oracolo $O_f$ aggiunge una fase negativa a qualsiasi soluzione al problema di ricerca. Pertanto, può essere scritto come reflection per l'asse $\ket{\text{bad}}$:

$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$

Analogamente, lo spostamento di fase condizionale $O_0$ è solo una reflection invertita per lo stato $\ket{0}$:

$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$

Conoscendo questo fatto, è facile verificare che anche l'operazione di diffusione di Grover $-H^{\otimes n} O_0 H^{\otimes n}$ è una reflection per lo stato $\ket{all}$. È sufficiente:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$

È stato dimostrato che ogni iterazione dell'algoritmo di Grover è una composizione di due reflection $R_\ket{\text{bad}}$ e $R_\ket{\text{all}}$.

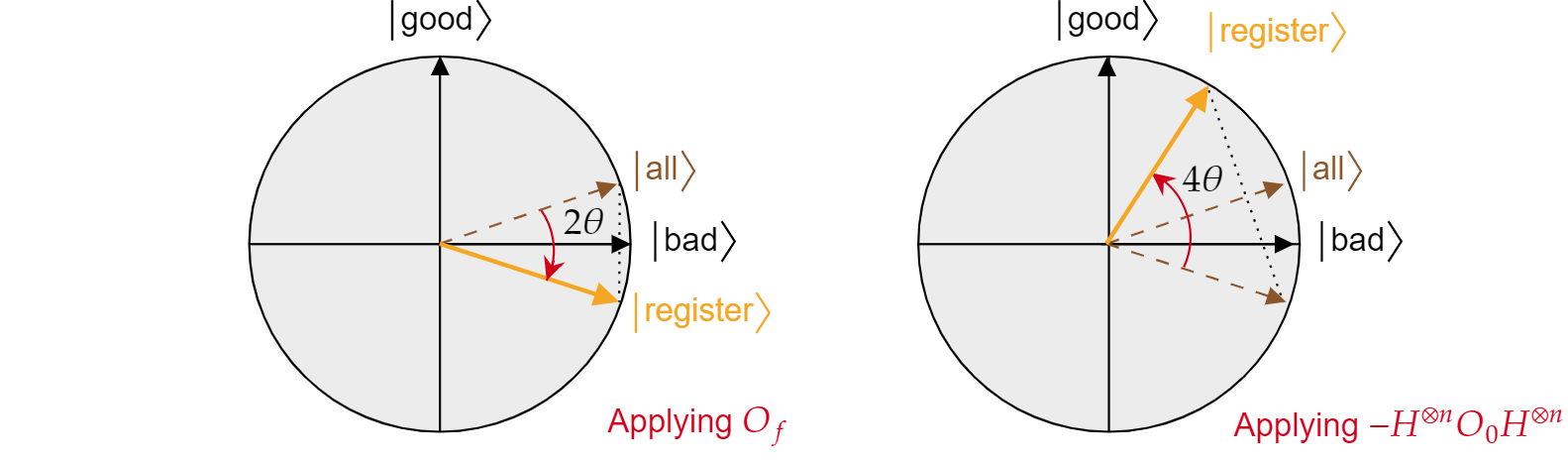
L'effetto combinato di ogni iterazione di Grover è una rotazione in senso antiorario di un angolo $2\theta$. Fortunatamente, l'angolo $\theta$ è facile da trovare. Poiché $\theta$ è semplicemente l'angolo tra $\ket{\text{all}}$ e $\ket{\text{bad}}$, è possibile usare il prodotto scalare per trovare l'angolo. È noto che $\cos{\theta}=\braket{\text{all}|\text{bad}}$, quindi è necessario calcolare $\braket{\text{all}|\text{bad}}$. Dalla scomposizione di $\ket{\text{all}}$ in termini di $\ket{\text{bad}}$ e $\ket{\text{good}}$ ne consegue:

$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

L'angolo tra lo stato del registro e lo $\ket{\text{stato buono}}$ diminuisce con ogni iterazione, causando una probabilità superiore di misurare un risultato valido. Per calcolare questa probabilità, è sufficiente calcolare $|\braket{\text{un}|\text{buon registro}}|^2$. Indicando l'angolo tra $\ket{\text{good}}$ e $\ket{\text{register}}$$\gamma (k)$ dove $k$ è il conteggio delle iterazioni:

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

Pertanto, la probabilità di successo è:

$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

Numero ottimale di iterazioni

Poiché la probabilità di successo può essere scritta come funzione del numero di iterazioni, il numero ottimale di iterazioni $N_{\text{optimal}}$ può essere trovato calcolando l'intero positivo più piccolo che (approssimativamente) ottimizza la funzione di probabilità di successo.

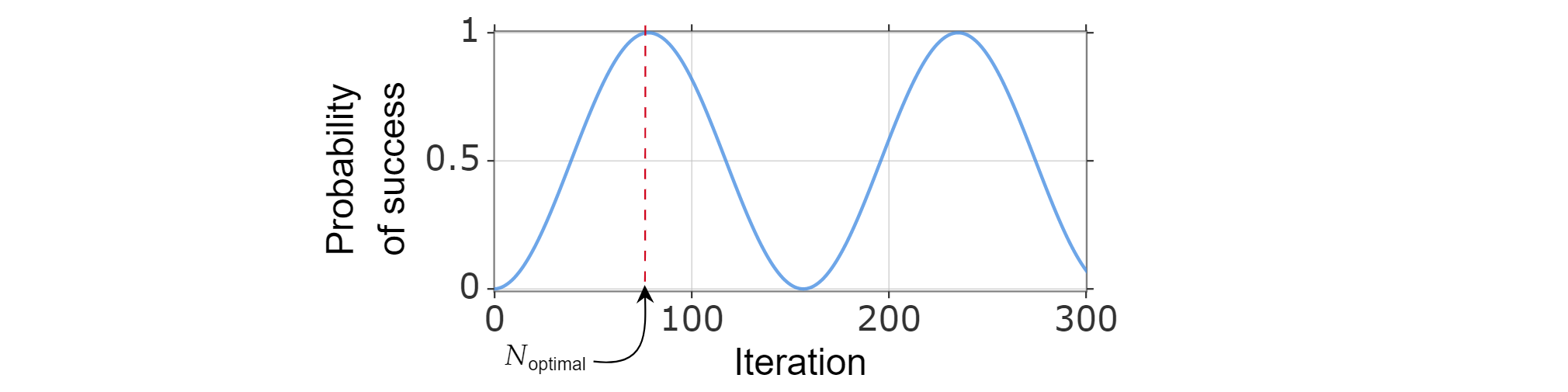
È noto che $\sin^2{x}$ raggiunge il primo massimo per $x=\frac{\pi}{2}$, quindi:

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Il risultato è il seguente:

$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$

Dove nell'ultimo passaggio $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.

È quindi possibile scegliere $N_\text{optimal}$ da $N_\text{optimal=\left}\l started \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{2}\right\r floor$.

Analisi della complessità

Dall'analisi precedente, le query $O\left(\sqrt{\frac{N}{M}}\right)$ dell'oracolo $O_f$ sono necessarie per trovare un elemento valido. Tuttavia, l'algoritmo può essere implementato in modo efficiente in termini di complessità temporale? $O_0$ è basato sul calcolo di operazioni booleane $su n$ bit ed è noto per essere implementabile tramite $O(n)$ porte. Esistono anche due livelli di $n$ porte di Hadamard. Entrambi questi componenti richiedono quindi solo $O(n)$ porte per ogni iterazione. Poiché $N2=^n$, ne consegue che $O(n)=O(log(N))$. Pertanto, se sono necessarie $O\left(\sqrt{\frac{N}{M}}\right)$ iterazioni e $O(log(N))$ porte per iterazione, la complessità del tempo totale (senza prendere in considerazione l'implementazione dell'oracolo) è $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.

La complessità complessiva dell'algoritmo dipende in definitiva dalla complessità dell'implementazione del O_f$ oracle$. Se una valutazione di funzione è molto più complessa in un computer quantistico rispetto a quella classica, il runtime complessivo dell'algoritmo sarà più lungo nel caso quantistico, anche se tecnicamente, usa meno query.

Riferimenti

Per altre informazioni sull'algoritmo di Grover, è possibile consultare le fonti seguenti:

• Documento originale di Lov K. Grover
• Sezione Algoritmi di ricerca quantistica di Nielsen, M. A. &Amp; Chuang, I. L. (2010). Quantum Computation and Quantum Information.
• Informazioni sull'algoritmo di Grover in Arxiv.org

Passaggi successivi

• Rappresentazione intermedia quantistica
• Vettori e matrici
• T gate e T factory
• Qubit multipli