Qubit nel calcolo quantistico
Proprio come i bit sono l'oggetto fondamentale delle informazioni nel calcolo classico, i qubit (bit quantistici) sono l'oggetto fondamentale delle informazioni nel calcolo quantistico. Per comprendere questa corrispondenza, questo articolo esamina l'esempio più semplice: un singolo qubit.
Rappresentazione di un qubit
Anche se un bit, o cifra binaria, può avere un valore pari a $0$ o $1$, un qubit può avere un valore pari a $0$, $1$ o una sovrapposizione quantistica pari a $0$ e $1$.
Lo stato di un singolo qubit può essere descritto da un vettore di colonna bidimensionale di norma unitaria, ovvero, la grandezza al quadrato delle voci deve essere sommata a $1$. Questo vettore, denominato vettore di stato quantistico, contiene tutte le informazioni necessarie per descrivere il sistema quantistico a qubit singolo proprio come un singolo bit contiene tutte le informazioni necessarie per descrivere lo stato di una variabile binaria. Per informazioni di base su vettori e matrici nel calcolo quantistico, vedere Vettori e matrici.
Qualsiasi vettore di colonna bidimensionale di numeri reali o complessi con norma $1$ rappresenta un possibile stato quantistico mantenuto da un qubit. Pertanto $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ rappresenta uno stato qubit se $\alpha$ e $\beta$ sono numeri complessi che soddisfano $|\alpha|^2 + |\beta|^2 = 1$. Alcuni esempi di vettori di stato quantistico validi che rappresentano qubit includono
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \begin{bmatrix}\frac{{1}{\sqrt{2}}\\\frac{{1}{\sqrt{2}}\end{bmatrix}, \begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{{-1}{\sqrt{2}}\end{bmatrix}, \text{ e }\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{i}{\sqrt{2}}\end{bmatrix}.$$
I vettori di stato quantistico $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ e $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ hanno un ruolo speciale. Questi due vettori formano una base per lo spazio vettoriale che descrive lo stato del qubit. Ciò significa che qualsiasi vettore di stato quantistico può essere scritto come somma di questi vettori di base. In particolare, il vettore $\begin{bmatrix} x \\ y \end{bmatrix}$ può essere scritto come $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Anche se qualsiasi rotazione di questi vettori fungerebbe da base perfettamente valida per il qubit, viene scelto questo in particolare e viene denominato base computazionale.
Questi due stati quantistici vengono selezionati per corrispondere ai due stati di un bit classico, ovvero $0$ e $1$. La convenzione standard prevede di scegliere
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
anche se potrebbe essere accolta ugualmente la scelta opposta. Di conseguenza, dal numero infinito di possibili vettori di stato quantistico a qubit singolo, solo due corrispondono agli stati dei bit classici; tutti gli altri stati quantistici non hanno corrispondenza.
Misurazione di un qubit
Per la rappresentazione di un qubit, è possibile ottenere un'idea di ciò che indicano questi stati illustrando il concetto di misurazione. Una misurazione corrisponde all'idea informale di "osservare" un qubit, che comprime immediatamente lo stato quantistico in uno dei due stati classici $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ o $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Quando viene misurato un qubit dato dal vettore di stato quantistico $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$, il risultato $0$ si ottiene con probabilità $|\alpha|^2$ e il risultato $1$con probabilità $|\beta|^2$. Nel risultato $0$, il nuovo stato del qubit è $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$; nel risultato $1$ lo stato è $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Si noti che queste probabilità sommano fino a $1$ a causa della condizione di normalizzazione $|\alpha|^2 + |\beta|^2 = 1$.
Le proprietà della misurazione indicano anche che il segno complessivo del vettore di stato quantistico è irrilevante. La negazione di un vettore è equivale a $\alpha\rightarrow -\alpha$ e $\beta\rightarrow -\beta$. Poiché la probabilità di misurare $0$ e $1$ dipende dalla grandezza al quadrato dei termini, l'inserimento di tali segni non modifica le probabilità. Queste fasi sono comunemente denominate "fasi globali" e più in generale possono avere il formato $e^{i \phi}$ anziché solo $\pm 1$.
Un'ultima importante proprietà della misurazione è che non danneggia necessariamente tutti i vettori di stato quantistico. Se si inizia con un qubit nello stato $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, che corrisponde allo stato classico $0$, la misurazione di questo stato restituisce sempre il risultato $0$ e lascia invariato lo stato quantistico. In questo senso, se sono presenti solo bit classici (ad esempio, qubit di tipo $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ o $\begin{bmatrix}0 \\ 1 \end{bmatrix}$), la misurazione non danneggia il sistema. Ciò significa che è possibile replicare i dati classici e modificarli in un computer quantistico esattamente come in un computer classico. La possibilità, tuttavia, di archiviare le informazioni in entrambi gli stati con una sola operazione è ciò che rende il calcolo quantistico preferibile rispetto a quello classico e priva ulteriormente i computer quantistici della possibilità di copiare i dati quantistici in modo indiscriminato, vedere anche il teorema di non clonazione.
Visualizzazione di qubit e trasformazioni tramite la sfera Bloch
I qubit possono anche essere raffigurati in $3D$ usando la rappresentazione della sfera di Bloch. La sfera di Bloch offre un modo per descrivere uno stato quantistico a qubit singolo (che è un vettore complesso bidimensionale) come vettore tridimensionale con valori reali. Questo è importante perché consente di visualizzare gli stati a qubit singolo e quindi sviluppare un ragionamento che può essere prezioso per comprendere gli stati a più qubit (dove purtroppo la rappresentazione della sfera di Bloch si interrompe). La sfera di Bloch può essere visualizzata come segue:
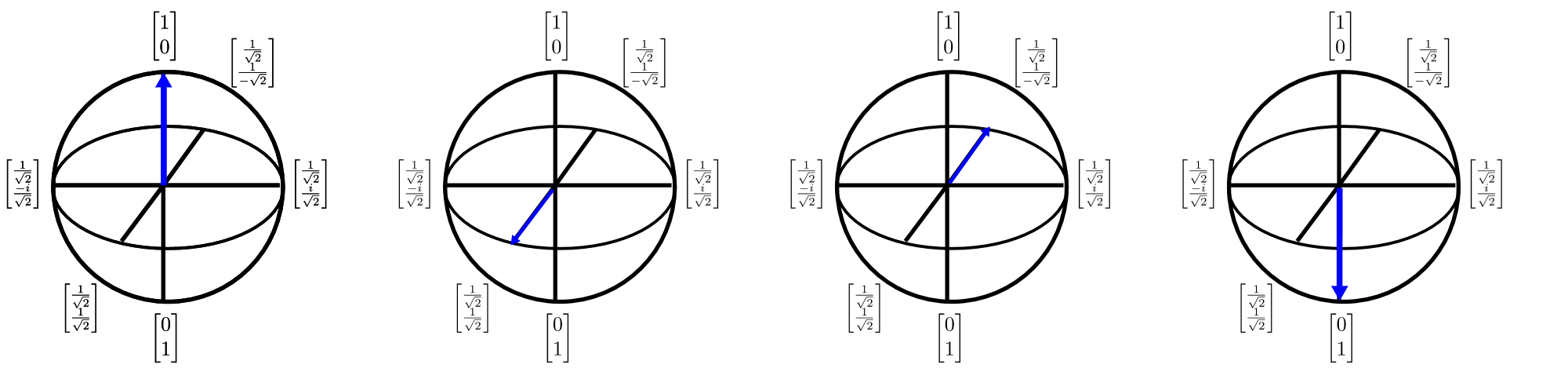
Le frecce in questo diagramma mostrano la direzione in cui punta il vettore di stato quantistico e ogni trasformazione della freccia può essere pensata come una rotazione su uno degli assi cardinali. Anche se pensare a un calcolo quantistico come una sequenza di rotazioni è un'idea potente, è difficile usare questa intuizione per progettare e descrivere gli algoritmi. Q# attenua questo problema fornendo un linguaggio per la descrizione di tali rotazioni.
Operazioni a qubit singolo
I computer quantistici elaborano i dati applicando un set universale di porte quantistiche in grado di emulare qualsiasi rotazione del vettore di stato quantistico. Questa nozione di universalità è simile alla nozione di universalità per il calcolo tradizionale (ad esempio, classico) in cui un set di porte è considerato universale se ogni trasformazione dei bit di input può essere eseguita usando un circuito di lunghezza finita. Nel calcolo quantistico, le trasformazioni valide che è possibile eseguire su un qubit sono trasformazioni e misurazioni unitarie. L'operazione contigua o la trasposizione coniugata complessa è di importanza fondamentale per il calcolo quantistico perché è necessario invertire le trasformazioni quantistiche.
Le operazioni a qubit singolo o i gate quantistici a qubit singolo possono essere classificati in due categorie: porte Clifford e porte non Clifford. I cancelli non Clifford sono costituiti solo da $T-gate$ (noto anche come $porta \pi/8$ ).
$$T=\begin{bmatrix} 1 amp; 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.& $$
Il set standard di porte Clifford a qubit singolo, incluso per impostazione predefinita in Q#, include
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 &\\ amp; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i &\\ amp; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix} 0\\ 0&-1 \end{bmatrix}=T^4. $$
In questo caso, le operazioni $X$, $Y$ e $Z$ vengono usate con particolare frequenza e sono denominate operatori Pauli dal nome del loro creatore, Wolfgang Pauli. Insieme alla porta non Clifford (la porta $T$), queste operazioni possono essere composte per approssimare qualsiasi trasformazione unitaria in un singolo qubit.
Mentre le precedenti costituiscono le porte primitive più diffuse per la descrizione delle operazioni a livello logico dello stack (si consideri il livello logico come il livello dell'algoritmo quantistico), è spesso utile prendere in considerazione operazioni meno di base a livello algoritmico, ad esempio operazioni più vicine a un livello di descrizione della funzione. Fortunatamente, in Q# sono disponibili anche metodi per l'implementazione di unità di livello superiore, che, a loro volta, consentono l'implementazione di algoritmi di alto livello senza scomporre in modo esplicito ogni elemento fino alle porte Clifford e $T$.
La primitiva più semplice è la rotazione a qubit singolo. Vengono in genere considerate tre rotazioni a qubit singolo: $R_x$, $R_y$ e $R_z$. Per visualizzare l'azione della rotazione $R_x(\theta),$ ad esempio, si supponga di puntare il pollice destro lungo la direzione dell'asse $x$ della sfera di Bloch e di ruotare il vettore con la mano in un angolo di $\theta/2$ radianti. Questo fattore di confusione di $2$ deriva dal fatto che i vettori ortogonali sono distanti $180^\circ$ se tracciati sulla sfera di Bloch, ma in realtà sono a $90^\circ$ di distanza geometricamente. Le matrici unitarie corrispondenti sono:
\begin{align*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2&}amp; 0 0\\& amp; e^{i\theta/2\end{bmatrix}}, \\& R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H\begin{bmatrix} =\cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) amp; \cos(\theta/2) \end{bmatrix}&, \\& = R_y(\theta) e^{-i\theta Y/2=} SHR_z(\theta)HS^\begin{bmatrix}\dagger= \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) amp; \cos(\theta/2) &\end{bmatrix}. = \end{align*}
Così come è possibile combinare tre rotazioni per eseguire una rotazione arbitraria in tre dimensioni, è possibile vedere dalla rappresentazione della sfera di Bloch che qualsiasi matrice unitaria può essere scritta anche come sequenza di tre rotazioni. In particolare, per ogni matrice unitaria $U$ esiste $\alpha,\beta,\gamma,\delta$ in modo che $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Quindi $R_z(\theta)$ e $H$ formano anche un set di porte universali, anche se non è un set discreto perché $\theta$ può assumere qualsiasi valore. Per questo motivo, e a causa delle applicazioni nella simulazione quantistica, tali porte continue sono fondamentali per il calcolo quantistico, in particolare a livello di progettazione dell'algoritmo quantistico. Per ottenere l'implementazione hardware a tolleranza di errore, verranno infine compilate in sequenze di porte discrete che si avvicinano a queste rotazioni.