次の方法で共有

量子回路図の表記規則

  • [アーティクル]

量子アルゴリズムは、等価の書き込み行列表現よりも、回路図で理解しやすい場合があります。 この記事では、量子回路図とその規則を読み取る方法について説明します。

詳細については、「 量子回路図を視覚化する方法を参照してください。

量子回路図の読み取り

量子回路では、時間は左から右に流れます。 量子ゲートは時系列順に並べられ、量子ビットに最初に適用されたゲートが一番左に記述されます。

次の量子回路図を例として見てみましょう。

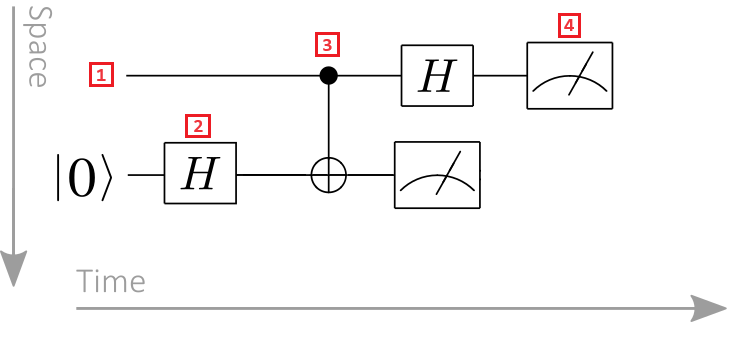
2つのレジスタ、1つのハダマールゲート、1つの制御ゲートと1つの測定を備えた量子回路の図。

  1. 量子ビット レジスタ: 量子ビット レジスタは水平線として表示され、各行は量子ビットを表します。 一番上の行には 0 というラベルが付いた量子ビット レジスタ、2 番目の行には 1 というラベルが付いた量子ビット レジスタがあります。
  2. 量子ゲート: 量子演算は、 量子ゲートで表されます。 量子ゲートという用語は、従来の論理ゲートと似ています。 1 つ以上の量子ビット レジスタで動作するゲートは、ボックスとして示されます。 この例では、シンボルは Hadmard 操作を表します。
  3. 制御ゲート: 制御ゲートは 2 つ以上の量子ビットに作用します。 この例では、シンボルは CNOT ゲートを表しています。 黒い円は制御量子ビットを表し、円内の十字は target 量子ビットを表します。
  4. 測定操作: 測定記号は測定操作を表します。 測定操作では、量子ビット レジスタを入力として受け取り、従来の情報を出力します。

量子ゲートの適用

時間は左から右に流れるので、最も左のゲートが最初に適用されます。たとえば、次の量子回路のアクションはユニタリ 行列 $CBA$です。

量子回路で左から右に適用されている量子ゲートの図。

Note

行列乗算では、正反対の規則に従います。つまり、右端の行列が最初に適用されます。 ただし、量子回路図では、一番左のゲートが最初に適用されます。 この違いによって混乱が生じる場合があるため、線形代数表記と量子回路図のこの大きな違いを銘記しておくことは重要です。

量子回路の入力と出力

量子回路図では、量子ゲートに入るワイヤは量子ゲートに入力される量子ビットを表し、量子ゲートから出るワイヤは量子ゲートから出力される量子ビットを表します。

量子ゲートの入力数は、量子ゲートの出力数と等しくなります。 これは、量子演算がユニタリであるため、元に戻すことができるためです。 量子ゲートが入力よりも多くの出力を持っていた場合、それは元に戻すことはできません。したがって、ユニタリではありません。これは矛盾です。

このため、回路図に記述されるすべてのボックスには、それを終了するときとまったく同じ数のワイヤを入力する必要があります。

マルチ量子ビット操作

マルチ量子ビットの回路図は、単一の量子ビットの回路図と同様の規則に従います。 たとえば、2 量子ビットのユニタリ演算 $B$ を $(H S\otimes X)$に定義できるため、同等の量子回路は次のようになります。

2 量子ビットユニタリ演算の回路図。

また、回路が使用されているコンテキストによっては、単一量子ビットの 2 つのレジスタではなく、2 量子ビットの単一レジスタに対する動作を含むように $B$ を表示することもできます。

このような抽象回路図の中で最も役に立つ特性として、基本ゲートにコンパイルする必要なしに、複雑な量子アルゴリズムを大まかに記述できる点を挙げることができます。 つまり、アルゴリズム内の各サブルーチンがどのように機能するかについて事細かに理解する必要なしに、大規模な量子アルゴリズムのデータ フローを直感的に捉えることができます。

制御ゲート

量子制御ゲートは、制御量子ビットが特定の状態にある場合に、 target 量子ビットに単一量子ビット ゲートを適用する 2 量子ビット ゲートです。

たとえば、1 つの量子ビットの値によって $G$ 演算の適用が制御される、$\Lambda(G)$で示される量子制御ゲートについて考えます。 制御されたゲート $\Lambda(G)$ は、次の製品状態入力の例を参照して理解できます。

$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi} + \beta\ket{{1} G\ket{\psi}$

つまり、制御量子ビットが値 $1$ を取る場合のみ、制御ゲートにより $G$ が $\psi$ を含むレジスタに適用されます。 一般に、このような制御された操作は、次の記号によって回路図で説明されています。

1 つの制御されたゲートの回路図。

ここで、黒い円はゲートが制御される量子ビットを表し、垂直方向のワイヤは、制御量子ビットが値 $1$ を取るときに適用されるユニタリを表します。

$G=X$および$G=Z$特別なケースでは、制御されたバージョンのゲートを記述するために次の表記が使用されます (制御された X ゲートは CNOT ゲートであることに注意してください)。

制御ゲートの特殊なケースの回路図。

Q# では、制御されたバージョンの演算を自動的に生成するメソッドを提供します。これにより、プログラマはこれらの演算を手動でコーディングする必要がなくなります。 その例を以下に示します。

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

古典的に制御されたゲート

量子ゲートは、測定の後に適用することもできます。測定の結果は古典的な制御ビットとして機能します。

次の記号は、 $G$ が値 $1 である古典的な制御ビットに条件付きで適用される、古典的に制御されたゲートを表$。

制御された動作を表す回路図。

測定演算子

測定操作では、量子ビット レジスタを取得し、それを測定し、結果を古典的な情報として出力します。

測定演算は測定記号で示され、常に入力として量子ビット レジスタ (実線で示されます) を受け取り、古典的な情報を出力します (2 本の線で示されます)。 具体的には、測定操作のシンボルは次のようになります。

測定操作を表す記号。

Q#では、Measure演算子によって測定操作が実装されます。

例: ユニタリ変換

ユニタリ変換 $\text{ CNOT}_{01}(H\otimes 1)$ について考えてみます。 このゲート シーケンスは、2 量子ビットの最大限にもつれた状態を作り出すので、量子コンピューティングにとって基本的な意味を持ちます。

$\mathrm{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}}\left(\ket{{00} + \ket{11}\right),$

このような、またはこれ以上の複雑さを持つ演算は、量子アルゴリズムと量子エラー修正でよく見られます。

この最大限にもつれた量子状態を作り出す演算を回路図で表すと次のようになります。

最大エンタングルされた 2 量子ビット状態の回路図。

ハダマールゲートの背後にあるシンボルはCNOTゲートを表し、黒い円は制御量子ビットを示し、円内の十字は target 量子ビットを示します。 この量子回路は、2 量子ビット (すなわち、単一量子ビットで構成される 2 つのレジスタ) で動作するとして表されています。

例: テレポートの回路図

量子テレポーテーションは、回路コンポーネントを示す最適な量子アルゴリズムの 1 つです。

量子テレポーテーションは、送信側と受信側の間の共通の絡み合った状態と、それらの間の古典的な通信の助けを借りて、量子状態をある量子ビットから別の量子ビットに送信できるようにするプロトコルです。

学習目的では、送信者は Alice と呼ばれ、受信側は Bob と呼ばれ、テレポートされる量子ビットはメッセージ量子ビットと呼ばれます。 Alice と Bob はそれぞれ 1 量子ビットを保持し、Alice にはメッセージ量子ビットである余分な量子ビットがあります。

次の回路図は、テレポート プロトコルを示しています。

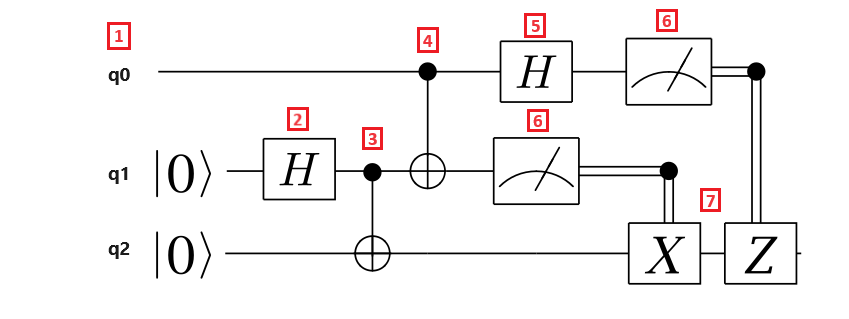
テレポーテーション プロトコルの量子回路の図。

テレポート プロトコルの手順を次に示します。

  1. 量子ビット レジスタ q0 はメッセージ量子ビット、量子ビット レジスタ q1 は Alice の量子ビット、量子ビット レジスタ q2 は Bob の量子ビットです。 メッセージ量子ビットは不明な状態で、Alice と Bob の量子ビットは $\ket{0}$ 状態です。
  2. Hadamard ゲートは、Alice の量子ビットに適用されます。 量子ビットは $\ket{0}$ 状態であるため、結果の状態は $\frac{1}{\sqrt{{2}}(\ket{{0} + \ket{1})$。
  3. CNOT ゲートは、Alice と Bob の量子ビットに適用されます。 Alice の量子ビットは制御量子ビット、Bob の量子ビットは target 量子ビットです。 結果の状態は $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$です。 Alice と Bob は、絡み合った状態を共有するようになりました。
  4. CNOT ゲートは、message 量子ビットと Alice の量子ビットに適用されます。 Alice の量子ビットも Bob の量子ビットと絡み合っているため、結果の状態は 3 量子ビットのエンタングル状態になります。
  5. Hadamard ゲートは、message 量子ビットに適用されます。
  6. Alice measures 彼女の 2 つの量子ビットと、回路に反映されていない Bob に測定結果を伝えます。 測定結果は 2 つの古典的ビットであり、値 00、01、10、または 11 を受け取ることができます。
  7. 古典的に制御された 2 つの Pauli ゲート X と Z は、 Bob の量子ビットに適用されます結果ビットの値 $1$。 結果の状態は、元のメッセージ量子ビット状態です。

関連するコンテンツ