회전
많은 CAD 애플리케이션은 클라이언트 영역에서 그린 개체를 회전하는 기능을 제공합니다. 회전 기능을 포함하는 애플리케이션은 SetWorldTransform 함수를 사용하여 적절한 월드 공간을 페이지 공간 변환으로 설정합니다. 이 함수는 적절한 값을 포함하는 XFORM 구조체에 대한 포인터를 받습니다. XFORM의 eM11, eM12, eM21 및 eM22 멤버는 회전 각도의 코사인, 사인, 음수 사인 및 코사인을 각각 지정합니다.
회전이 발생하면 개체를 구성하는 점이 좌표 공간 원점과 관련하여 회전됩니다. 다음 그림에서는 세계 좌표 공간에서 페이지 좌표 공간으로 복사할 때 30도 회전된 20 x 20 단위 사각형을 보여 줍니다.

앞의 그림에서 사각형의 각 지점은 좌표 공간 원점과 관련하여 30도 회전되었습니다.
다음 알고리즘은 좌표 공간 원점과 관련하여 각도 A로 회전되는 점(x,y)에 대한 새 x 좌표(x ')를 계산합니다.
x' = (x * cos A) - (y * sin A)
다음 알고리즘은 원점과 관련하여 A 각도로 회전되는 점(x,y)에 대한 y 좌표(y ')를 계산합니다.
y' = (x * sin A) + (y * cos A)
두 회전 변환은 다음과 같이 2-by-2 행렬로 결합할 수 있습니다.
|x' y'| == |x y| * | cos A sin A|
|-sin A cos A|
회전을 생성한 2 x 2 행렬에는 다음 값이 포함됩니다.
| .8660 .5000|
|-.5000 .8660|
회전 알고리즘은 두 각도의 합계(A1 및 A2)의 삼각 함수를 두 각도의 삼각 함수로 표현할 수 있음을 나타내는 trigonometry의 추가 정리를 기반으로 합니다.
sin(A1 + A2) = (sin A1 * cos A2) + (cos A1 * sin A2)
cos(A1 + A2) = (cos A1 * cos A2) - (sin A1 * sin A2)
다음 그림에서는 새 위치 p'에 대해 시계 반대 방향으로 회전된 점 p를 보여 줍니다. 또한 좌표 공간 원점에서 각 지점으로 그린 선과 x축을 통해 각 지점에서 그린 선으로 형성된 두 개의 삼각형을 보여 줍니다.
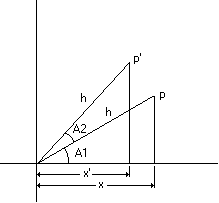
삼각을 사용하면 p 점의 x 좌표를 a1의 코사인에 의해 hypotenuse h의 길이를 곱하여 얻을 수 있습니다.
x = h * cos A1
p 점의 y 좌표는 hypotenuse h의 길이를 A1의 사인에 곱하여 얻을 수 있습니다.
y = h * sin A1
마찬가지로 p' 포인트의 x 좌표는 hypotenuse h의 길이를 의 코사인(A1 +A2)에 곱하여 얻을 수 있습니다.
x' = h * cos (A1 + A2)
마지막으로, p'포인트의 y 좌표는 (A1 +A2)의 사인을 통해 hypotenuse h의 길이를 곱하여 얻을 수 있습니다.
y' = h * sin (A1 + A2)
추가 정리를 사용하여 이전 알고리즘은 다음과 같습니다.
x' = (h * cos A1 * cos A2) - (h * sin A1 * sin A2)
y' = (h * cos A1 * sin A2) + (h * sin A1 * cos A2)
각도 A2로 회전된 지정된 지점에 대한 회전 알고리즘은 각 발생(h * cos A1)에 대해 x를 대체하고 각 발생에 대해 y를 대체하여 얻을 수 있습니다(h * sin A1 ).
x' = (x * cos A2) - (y * sin A2)
y' = (x * sin A2) + (y * cos A2)