Resultaten van geautomatiseerd machine learning-experiment evalueren

In dit artikel leert u hoe u modellen evalueert en vergelijkt die zijn getraind door uw geautomatiseerde machine learning-experiment (geautomatiseerde ML). In de loop van een geautomatiseerd ML-experiment worden veel taken gemaakt en elke taak maakt een model. Voor elk model genereert geautomatiseerde ML metrische evaluatiegegevens en -grafieken die u helpen de prestaties van het model te meten. U kunt verder een verantwoordelijk AI-dashboard genereren om standaard een holistische evaluatie en foutopsporing van het aanbevolen beste model uit te voeren. Dit omvat inzichten zoals modeluitleg, billijkheid en performance explorer, data explorer, modelfoutanalyse. Meer informatie over hoe u een verantwoordelijk AI-dashboard kunt genereren.

Met geautomatiseerde ML worden bijvoorbeeld de volgende grafieken gegenereerd op basis van het experimenttype.

Classificatie	Regressie/prognose
Verwarringsmatrix	Residuenhistogram
ROC-curve (Receiver Operating Characteristic)	Voorspeld versus waar
PR-curve (curve van intrekprecisie)	Prognosehorizk
Liftcurve
Cumulatieve winstcurve
Kalibratiecurve

Belangrijk

Items die in dit artikel zijn gemarkeerd (preview) zijn momenteel beschikbaar als openbare preview. De preview-versie wordt aangeboden zonder Service Level Agreement en wordt niet aanbevolen voor productieworkloads. Misschien worden bepaalde functies niet ondersteund of zijn de mogelijkheden ervan beperkt. Zie Aanvullende gebruiksvoorwaarden voor Microsoft Azure-previews voor meer informatie.

Vereisten

• Een Azure-abonnement. (Als u geen Azure-abonnement hebt, maakt u een gratis account voordat u begint)
• Een Azure Machine Learning-experiment dat is gemaakt met:
  • De Azure Machine Learning-studio (geen code vereist)
  • De Azure Machine Learning Python SDK

Taakresultaten weergeven

Nadat uw geautomatiseerde ML-experiment is voltooid, kunt u een geschiedenis van de taken vinden via:

• Een browser met Azure Machine Learning-studio
• Een Jupyter-notebook met behulp van de Jupyter-widget JobDetails

In de volgende stappen en video ziet u hoe u de metrische gegevens en grafieken van de uitvoeringsgeschiedenis en modelevaluatie in de studio kunt bekijken:

1. Meld u aan bij de studio en navigeer naar uw werkruimte.
2. Selecteer Taken in het linkermenu.
3. Selecteer uw experiment in de lijst met experimenten.
4. Selecteer in de tabel onder aan de pagina een geautomatiseerde ML-taak.
5. Selecteer op het tabblad Modellen de naam van het algoritme voor het model dat u wilt evalueren.
6. Gebruik op het tabblad Metrische gegevens de selectievakjes aan de linkerkant om metrische gegevens en grafieken weer te geven.

Metrische classificatiegegevens

Geautomatiseerde ML berekent metrische prestatiegegevens voor elk classificatiemodel dat voor uw experiment is gegenereerd. Deze metrische gegevens zijn gebaseerd op de scikit learn-implementatie.

Veel metrische classificatiegegevens worden gedefinieerd voor binaire classificatie in twee klassen en vereisen gemiddelde over klassen om één score voor classificatie met meerdere klassen te produceren. Scikit-learn biedt verschillende gemiddelde methoden, waarvan drie geautomatiseerde ML beschikbaar maakt: macro, micro en gewogen.

• Macro : de metrische waarde berekenen voor elke klasse en het niet-gewogen gemiddelde berekenen
• Micro : bereken de metrische waarde globaal door het totaal aantal terecht-positieven, fout-negatieven en fout-positieven te tellen (onafhankelijk van klassen).
• Gewogen: bereken de metrische waarde voor elke klasse en neem het gewogen gemiddelde op basis van het aantal steekproeven per klasse.

Hoewel elke gemiddelde methode zijn voordelen heeft, is een veelvoorkomende overweging bij het selecteren van de juiste methode een onevenwichtige klasse. Als klassen verschillende aantallen steekproeven hebben, is het misschien informatiever om een macrogemiddelde te gebruiken waarbij minderheidsklassen gelijke weging krijgen voor meerderheidsklassen. Meer informatie over binaire versus metrische gegevens van meerdere klassen in geautomatiseerde ML.

De volgende tabel bevat een overzicht van de metrische gegevens over modelprestaties die geautomatiseerde ML berekent voor elk classificatiemodel dat voor uw experiment is gegenereerd. Zie de scikit-learn-documentatie die is gekoppeld aan het berekeningsveld van elke metrische waarde voor meer informatie.

Notitie

Raadpleeg de sectie metrische afbeeldingsgegevens voor aanvullende informatie over metrische gegevens voor afbeeldingsclassificatiemodellen.

Metrisch	Beschrijving	Berekening
AUC	AUC is het gebied onder de ontvanger bedrijfseigenschapscurve. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1] Ondersteunde namen van metrische gegevens zijn onder andere, AUC_macro, het rekenkundige gemiddelde van de AUC voor elke klasse. AUC_micro, berekend door het totaal aantal terecht-positieven, fout-negatieven en fout-positieven te tellen. AUC_weighted, rekenkundig gemiddelde van de score voor elke klasse, gewogen door het aantal werkelijke exemplaren in elke klasse. AUC_binary, de waarde van AUC door één specifieke klasse als true klasse te behandelen en alle andere klassen als klasse te false combineren.	Berekening
accuracy	Nauwkeurigheid is de verhouding tussen voorspellingen die exact overeenkomen met de werkelijke klasselabels. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1]	Berekening
average_precision	De gemiddelde precisie geeft een overzicht van een precisieherhalingscurve als het gewogen gemiddelde van precisies die bij elke drempelwaarde zijn bereikt, met de toename van de relevante overeenkomsten van de vorige drempelwaarde die als gewicht wordt gebruikt. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1] Ondersteunde namen van metrische gegevens zijn onder andere, average_precision_score_macro, het rekenkundige gemiddelde van de gemiddelde precisiescore van elke klasse. average_precision_score_micro, berekend door het totaal aantal terecht-positieven, fout-negatieven en fout-positieven te tellen. average_precision_score_weighted, het rekenkundige gemiddelde van de gemiddelde precisiescore voor elke klasse, gewogen door het aantal werkelijke exemplaren in elke klasse. average_precision_score_binary, de waarde van gemiddelde precisie door één specifieke klasse als true klasse te behandelen en alle andere klassen als klasse te false combineren.	Berekening
balanced_accuracy	Evenwichtige nauwkeurigheid is het rekenkundige gemiddelde van relevante overeenkomsten voor elke klasse. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1]	Berekening
f1_score	F1 score is het harmonische gemiddelde van precisie en relevante overeenkomsten. Het is een evenwichtige meting van zowel fout-positieven als fout-negatieven. Er wordt echter geen rekening gehouden met echte negatieven. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1] Ondersteunde namen van metrische gegevens zijn onder andere, f1_score_macro: het rekenkundige gemiddelde van de F1-score voor elke klasse. f1_score_micro: berekend door het totaal aantal terecht-positieven, fout-negatieven en fout-positieven te tellen. f1_score_weighted: gewogen gemiddelde met klassefrequentie van F1-score voor elke klasse. f1_score_binary, de waarde van f1 door één specifieke klasse als true klasse te behandelen en alle andere klassen als klasse te false combineren.	Berekening
log_loss	Dit is de verliesfunctie die wordt gebruikt in (multinomiale) logistieke regressie en uitbreidingen ervan, zoals neurale netwerken, gedefinieerd als de negatieve logboekkans van de werkelijke labels op basis van de voorspellingen van een probabilistische classificatie. Doelstelling: Dichter bij 0 hoe beter Bereik: [0, inf)	Berekening
norm_macro_recall	Genormaliseerde macroherhaling is terughalen van macrogemiddelde en genormaliseerd, zodat willekeurige prestaties een score van 0 hebben en de perfecte prestaties een score van 1 hebben. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1]	(recall_score_macro - R) / (1 - R) waarbij de R verwachte waarde voor recall_score_macro willekeurige voorspellingen is. R = 0.5 voor binaire classificatie. R = (1 / C) voor C-klasseclassificatieproblemen.
matthews_correlation	Matthews correlatiecoëfficiënt is een evenwichtige meting van nauwkeurigheid, die zelfs kan worden gebruikt als één klasse veel meer steekproeven heeft dan een andere klasse. Een coëfficiënt van 1 geeft perfecte voorspelling, 0 willekeurige voorspelling en -1 inverse voorspelling aan. Doelstelling: Dichter bij 1 hoe beter Bereik: [-1, 1]	Berekening
precisie	Precisie is de mogelijkheid van een model om het labelen van negatieve steekproeven als positief te voorkomen. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1] Ondersteunde namen van metrische gegevens zijn onder andere, precision_score_macro, het rekenkundige gemiddelde van precisie voor elke klasse. precision_score_micro, globaal berekend door het totale aantal terecht-positieven en fout-positieven te tellen. precision_score_weighted, het rekenkundige gemiddelde van precisie voor elke klasse, gewogen met het aantal werkelijke exemplaren in elke klasse. precision_score_binary, de waarde van precisie door één specifieke klasse als true klasse te behandelen en alle andere klassen als klasse te false combineren.	Berekening
relevante overeenkomsten	Intrekken is de mogelijkheid van een model om alle positieve steekproeven te detecteren. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1] Ondersteunde namen van metrische gegevens zijn onder andere, recall_score_macro: het rekenkundige gemiddelde van relevante overeenkomsten voor elke klasse. recall_score_micro: globaal berekend door het totaal aantal terecht-positieven, fout-negatieven en fout-positieven te tellen. recall_score_weighted: het rekenkundige gemiddelde van relevante overeenkomsten voor elke klasse, gewogen met het aantal werkelijke exemplaren in elke klasse. recall_score_binary, de waarde van relevante overeenkomsten door één specifieke klasse als true klasse te behandelen en alle andere klassen als klasse te false combineren.	Berekening
weighted_accuracy	Gewogen nauwkeurigheid is nauwkeurigheid waarbij elke steekproef wordt gewogen door het totale aantal monsters dat tot dezelfde klasse behoort. Doelstelling: Dichter bij 1 hoe beter Bereik: [0, 1]	Berekening

Binaire versus metrische gegevens voor classificatie met meerdere klassen

Geautomatiseerde ML detecteert automatisch of de gegevens binair zijn en stelt gebruikers ook in staat om metrische gegevens voor binaire classificatie te activeren, zelfs als de gegevens meerdere klassen hebben door een true klasse op te geven. Metrische gegevens voor classificatie van meerdere klassen worden gerapporteerd als een gegevensset twee of meer klassen heeft. Metrische gegevens voor binaire classificatie worden alleen gerapporteerd wanneer de gegevens binair zijn.

Opmerking: metrische gegevens voor classificatie met meerdere klassen zijn bedoeld voor classificatie met meerdere klassen. Wanneer deze metrische gegevens worden toegepast op een binaire gegevensset, behandelen deze metrische gegevens geen klasse als klasse true , zoals u zou verwachten. Metrische gegevens die duidelijk zijn bedoeld voor meerdere klassen, worden voorzien microvan , macroof weighted. Voorbeelden zijn onder andere average_precision_score, f1_score, precision_score, recall_scoreen AUC. In plaats van bijvoorbeeld relevante overeenkomsten te berekenen als tp / (tp + fn), worden de gemiddelden van de multiklasse (micro, macroof weighted) in beide klassen van een binaire classificatiegegevensset berekend. Dit komt overeen met het berekenen van de relevante overeenkomsten voor de true klasse en de false klasse afzonderlijk en neemt vervolgens het gemiddelde van de twee.

Hoewel automatische detectie van binaire classificatie wordt ondersteund, wordt het nog steeds aanbevolen om de true klasse handmatig op te geven om ervoor te zorgen dat de metrische gegevens voor binaire classificatie worden berekend voor de juiste klasse.

Als u metrische gegevens voor binaire classificatiegegevenssets wilt activeren wanneer de gegevensset zelf meerdere klassen is, hoeven gebruikers alleen de klasse op te geven die moet worden behandeld als true klasse en deze metrische gegevens worden berekend.

Verwarringsmatrix

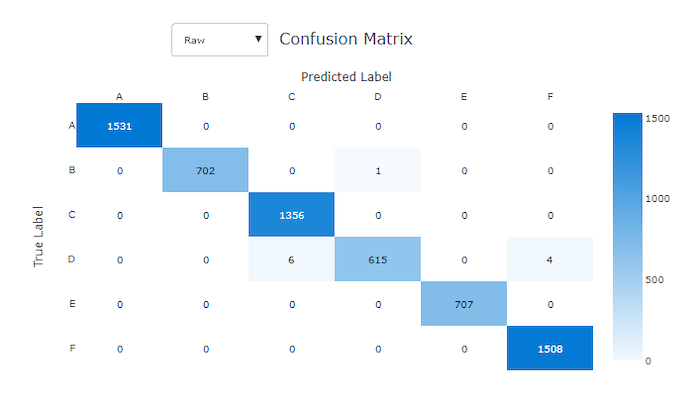
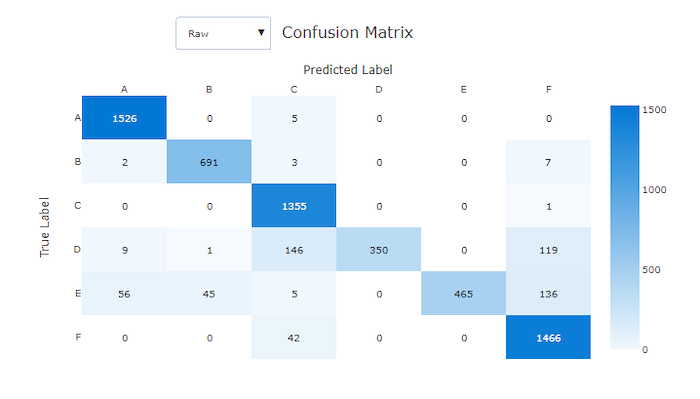
Verwarringsmatrices bieden een visual voor hoe een machine learning-model systematische fouten maakt in de voorspellingen voor classificatiemodellen. Het woord 'verwarring' in de naam komt van een model 'verwarrend' of verkeerd labelen voorbeelden. Een cel in rij i en kolom j in een verwarringsmatrix bevat het aantal voorbeelden in de evaluatiegegevensset die deel uitmaken van klasse C_i en worden geclassificeerd door het model als klasse C_j.

In de studio geeft een donkere cel een hoger aantal steekproeven aan. Het selecteren van de genormaliseerde weergave in de vervolgkeuzelijst normaliseert over elke matrixrij om het percentage van de klasse C_i weer te geven dat is voorspeld als klasse C_j. Het voordeel van de standaard onbewerkte weergave is dat u kunt zien of onevenwichtigheid in de verdeling van werkelijke klassen ertoe heeft geleid dat het model steekproeven van de minderheidsklasse verkeerd classificeert, een veelvoorkomend probleem bij onevenwichtige gegevenssets.

De verwarringsmatrix van een goed model bevat de meeste steekproeven langs de diagonale.

Verwarringsmatrix voor een goed model

Verwarringsmatrix voor een slecht model

ROC-curve

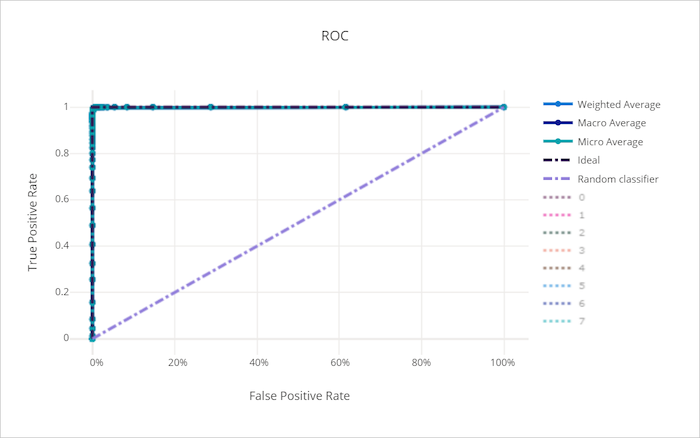
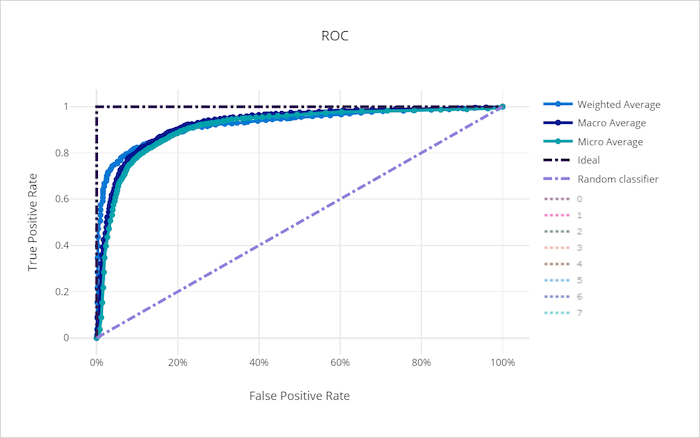
Met de ROC-curve (Receiver Operating Characteristic) wordt de relatie tussen de werkelijke positieve snelheid (TPR) en het fout-positieve tarief (FPR) uitgelijnd naarmate de beslissingsdrempel verandert. De ROC-curve kan minder informatief zijn wanneer trainingsmodellen op gegevenssets met een onevenwichtige klasse zijn, omdat de meerderheidsklasse bijdragen van minderheidsklassen kan verdrinken.

Het gebied onder de curve (AUC) kan worden geïnterpreteerd als het aandeel van correct geclassificeerde monsters. Nauwkeuriger is de AUC de kans dat de classificatie een willekeurig gekozen positieve steekproef hoger rangschikt dan een willekeurig gekozen negatieve steekproef. De vorm van de curve geeft een intuïtieve relatie tussen TPR en FPR als functie van de classificatiedrempel of beslissingsgrens.

Een curve die de linkerbovenhoek van de grafiek nadert, nadert een 100% TPR en 0% FPR, het best mogelijke model. Een willekeurig model produceert een ROC-curve langs de y = x lijn van de linkerbenedenhoek naar de rechterbovenhoek. Een slechter dan willekeurig model zou een ROC-curve hebben die onder de y = x lijn duikt.

Tip

Voor classificatieexperimenten kan elk van de lijndiagrammen die voor geautomatiseerde ML-modellen worden geproduceerd, worden gebruikt om het model per klasse of gemiddeld te evalueren voor alle klassen. U kunt schakelen tussen deze verschillende weergaven door te klikken op klasselabels in de legenda rechts van de grafiek.

ROC-curve voor een goed model

ROC-curve voor een slecht model

Precisie-relevante curve

De precisie-relevante curve plot de relatie tussen precisie en relevante overeenkomsten naarmate de beslissingsdrempel verandert. Intrekken is de mogelijkheid van een model om alle positieve steekproeven te detecteren en precisie is de mogelijkheid van een model om negatieve steekproeven als positief te labelen. Sommige zakelijke problemen vereisen mogelijk een hogere relevante overeenkomsten en een hogere precisie, afhankelijk van het relatieve belang van het vermijden van fout-negatieven versus fout-positieven.

Tip

Voor classificatieexperimenten kan elk van de lijndiagrammen die voor geautomatiseerde ML-modellen worden geproduceerd, worden gebruikt om het model per klasse of gemiddeld te evalueren voor alle klassen. U kunt schakelen tussen deze verschillende weergaven door te klikken op klasselabels in de legenda rechts van de grafiek.

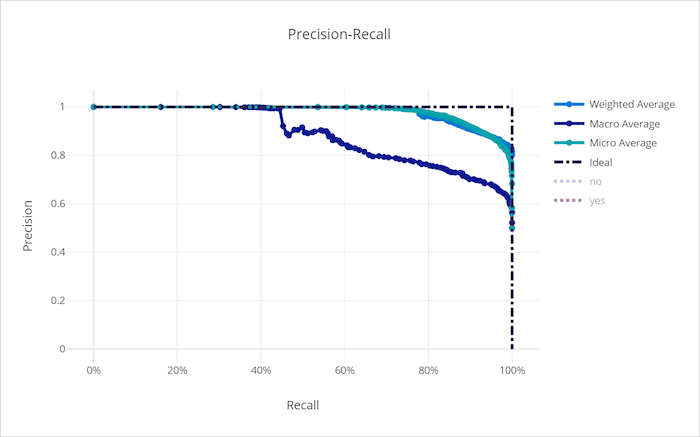
Precisieherhalingscurve voor een goed model

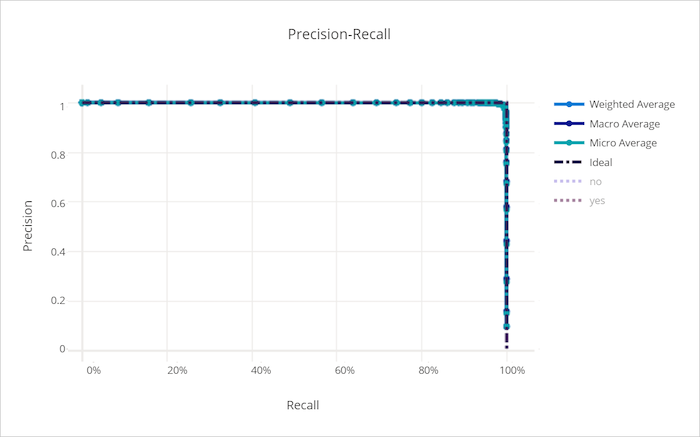
Precisieherhalingscurve voor een slecht model

Cumulatieve winstcurve

De cumulatieve toenamecurve plot het percentage positieve steekproeven dat correct is geclassificeerd als een functie van het percentage monsters dat wordt overwogen wanneer we steekproeven in de volgorde van de voorspelde waarschijnlijkheid beschouwen.

Als u winst wilt berekenen, sorteert u eerst alle steekproeven van hoogste naar laagste waarschijnlijkheid die door het model wordt voorspeld. x% Neem vervolgens de hoogste betrouwbaarheidsvoorspellingen. Deel het aantal positieve steekproeven dat x% is gedetecteerd door het totale aantal positieve steekproeven om de winst te verkrijgen. Cumulatieve winst is het percentage positieve steekproeven dat we detecteren bij het overwegen van een deel van de gegevens die waarschijnlijk tot de positieve klasse behoren.

Een perfect model rangschikt alle positieve steekproeven bovenal negatieve monsters die een cumulatieve toenamecurve van twee rechte segmenten geven. De eerste is een lijn met helling 1 / x van (0, 0) tot (x, 1) waar x het deel van de monsters is die deel uitmaken van de positieve klasse (1 / num_classes als klassen evenwichtig zijn). De tweede is een horizontale lijn van (x, 1) naar (1, 1). In het eerste segment worden alle positieve monsters correct geclassificeerd en de cumulatieve toename gaat naar 100% binnen de eerste x% van de overwogen monsters.

Het willekeurige basislijnmodel heeft een cumulatieve toenamecurve, waarbij y = x voor x% monsters alleen over x% het totale positieve aantal steekproeven werd gedetecteerd. Een perfect model voor een evenwichtige gegevensset heeft een microgemiddelde curve en een macrogemiddelde lijn met helling num_classes tot cumulatieve toename is 100% en vervolgens horizontaal totdat het gegevenspercentage 100 is.

Tip

Voor classificatieexperimenten kan elk van de lijndiagrammen die voor geautomatiseerde ML-modellen worden geproduceerd, worden gebruikt om het model per klasse of gemiddeld te evalueren voor alle klassen. U kunt schakelen tussen deze verschillende weergaven door te klikken op klasselabels in de legenda rechts van de grafiek.

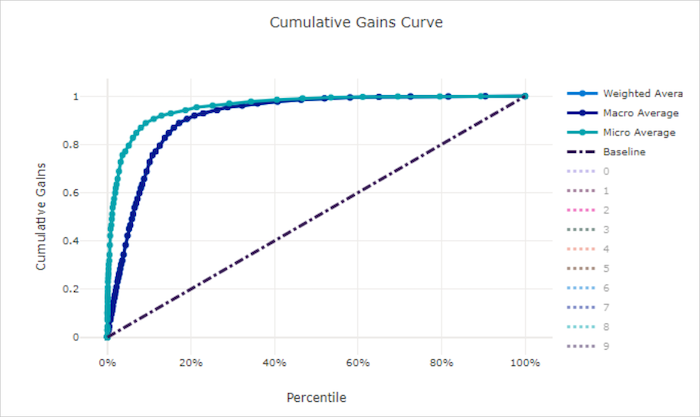
Cumulatieve winstcurve voor een goed model

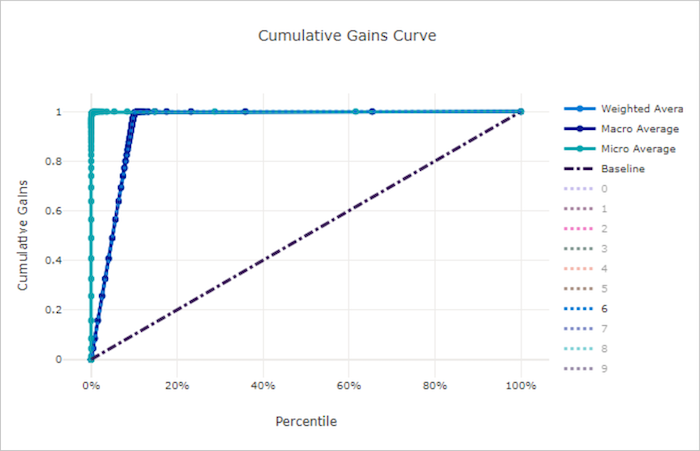
Cumulatieve winstcurve voor een slecht model

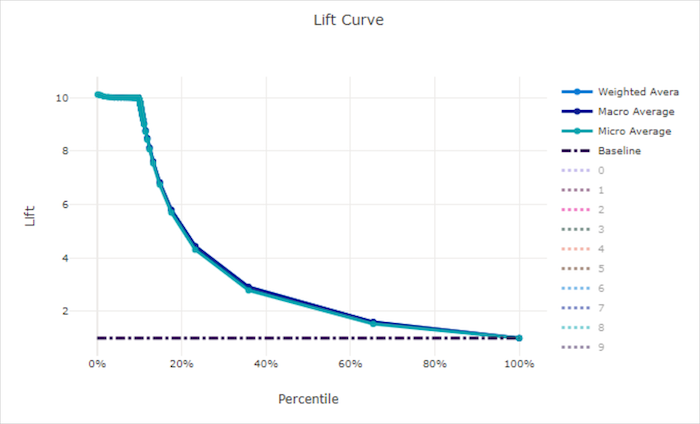
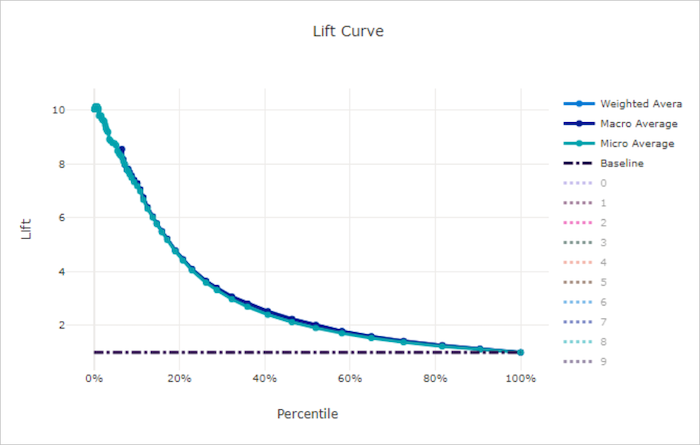
Liftcurve

De liftcurve laat zien hoe vaak beter een model presteert in vergelijking met een willekeurig model. Lift wordt gedefinieerd als de verhouding van cumulatieve toename tot de cumulatieve toename van een willekeurig model (dat altijd moet zijn 1).

Bij deze relatieve prestaties wordt rekening gehouden met het feit dat classificatie moeilijker wordt wanneer u het aantal klassen verhoogt. (Een willekeurig model voorspelt een hogere fractie van steekproeven uit een gegevensset met 10 klassen vergeleken met een gegevensset met twee klassen)

De liftcurve van de basislijn is de y = 1 lijn waarin de modelprestaties consistent zijn met die van een willekeurig model. Over het algemeen is de liftcurve voor een goed model hoger in dat diagram en verder van de x-as, wat laat zien dat wanneer het model het meeste vertrouwen heeft in de voorspellingen, het vele malen beter presteert dan willekeurig raden.

Tip

Voor classificatieexperimenten kan elk van de lijndiagrammen die voor geautomatiseerde ML-modellen worden geproduceerd, worden gebruikt om het model per klasse of gemiddeld te evalueren voor alle klassen. U kunt schakelen tussen deze verschillende weergaven door te klikken op klasselabels in de legenda rechts van de grafiek.

Lift curve voor een goed model

Lift curve voor een slecht model

Kalibratiecurve

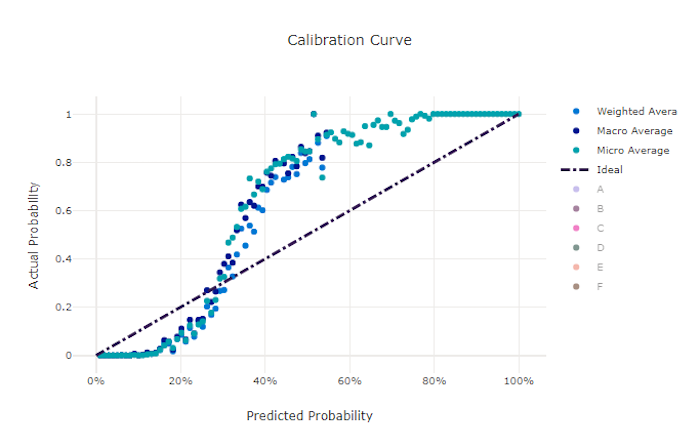
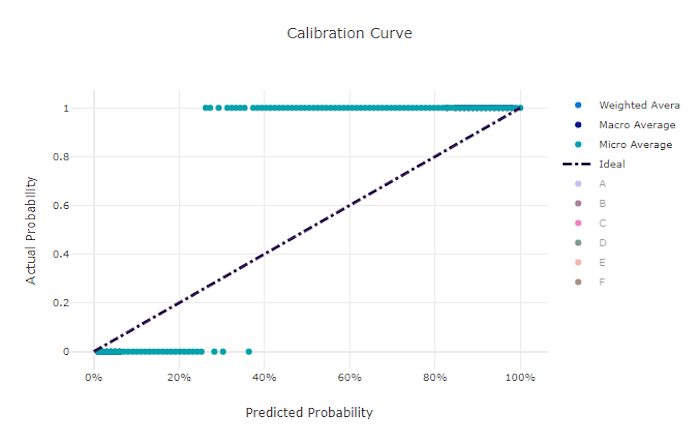
De kalibratiecurve plot het vertrouwen van een model in de voorspellingen ten opzichte van het aandeel positieve monsters op elk betrouwbaarheidsniveau. Een goed gekalibreerd model classificeert 100% van de voorspellingen waaraan het 100% betrouwbaarheid toewijst, 50% van de voorspellingen die het toewijst 50% betrouwbaarheid, 20% van de voorspellingen waaraan een betrouwbaarheid van 20% wordt toegewezen, enzovoort. Een perfect gekalibreerd model heeft een kalibratiecurve na de y = x lijn waar het model perfect de kans voorspelt dat monsters bij elke klasse horen.

Een te zeker model over-voorspelt waarschijnlijkheden dicht bij nul en één, zelden onzeker over de klasse van elke steekproef en de kalibratiecurve ziet er ongeveer als achterwaarts "S" uit. Een onderzeker model wijst gemiddeld een lagere waarschijnlijkheid toe aan de klasse die het voorspelt en de bijbehorende kalibratiecurve lijkt op een 'S'. De kalibratiecurve toont niet de mogelijkheid van een model om correct te classificeren, maar in plaats daarvan is het vermogen om vertrouwen correct toe te wijzen aan de voorspellingen. Een slecht model kan nog steeds een goede kalibratiecurve hebben als het model een lage betrouwbaarheid en hoge onzekerheid correct toewijst.

Notitie

De kalibratiecurve is gevoelig voor het aantal monsters, dus een kleine validatieset kan luidruchtige resultaten produceren die moeilijk te interpreteren zijn. Dit betekent niet noodzakelijkerwijs dat het model niet goed gekalibreerd is.

Kalibratiecurve voor een goed model

Kalibratiecurve voor een slecht model

Metrische gegevens voor regressie/prognose

Geautomatiseerde ML berekent dezelfde prestatiemetrieken voor elk gegenereerd model, ongeacht of het een regressie- of prognoseexperiment is. Deze metrische gegevens ondergaan ook normalisatie om vergelijking mogelijk te maken tussen modellen die zijn getraind op gegevens met verschillende bereiken. Zie normalisatie van metrische gegevens voor meer informatie.

De volgende tabel bevat een overzicht van de metrische gegevens voor modelprestaties die zijn gegenereerd voor regressie- en voorspellingsexperimenten. Net als metrische classificatiegegevens zijn deze metrische gegevens ook gebaseerd op de scikit learn-implementaties. De juiste scikit learn-documentatie wordt dienovereenkomstig gekoppeld in het veld Berekening .

Metrisch	Beschrijving	Berekening
explained_variance	De uitleg over variantie meet de mate waarin een model rekening maakt met de variatie in de doelvariabele. Dit is de procentdaling van de variantie van de oorspronkelijke gegevens tot de variantie van de fouten. Wanneer het gemiddelde van de fouten 0 is, is deze gelijk aan de bepalingscoëfficiënt (zie r2_score in de volgende grafiek). Doelstelling: Dichter bij 1 hoe beter Bereik: (-inf, 1]	Berekening
mean_absolute_error	Gemiddelde absolute fout is de verwachte waarde van de absolute waarde van het verschil tussen het doel en de voorspelling. Doelstelling: Dichter bij 0 hoe beter Bereik: [0, inf) Typen: mean_absolute_error normalized_mean_absolute_error, de mean_absolute_error gedeeld door het bereik van de gegevens.	Berekening
mean_absolute_percentage_error	Gemiddelde absolute percentagefout (MAPE) is een meting van het gemiddelde verschil tussen een voorspelde waarde en de werkelijke waarde. Doelstelling: Dichter bij 0 hoe beter Bereik: [0, inf)
median_absolute_error	Absolute mediaanfout is de mediaan van alle absolute verschillen tussen het doel en de voorspelling. Dit verlies is robuust voor uitbijters. Doelstelling: Dichter bij 0 hoe beter Bereik: [0, inf) Typen: median_absolute_error normalized_median_absolute_error: het median_absolute_error gedeeld door het bereik van de gegevens.	Berekening
r2_score	R2 (de bepalingscoëfficiënt) meet de proportionele vermindering in gemiddelde kwadratische fout (MSE) ten opzichte van de totale variantie van de waargenomen gegevens. Doelstelling: Dichter bij 1 hoe beter Bereik: [-1, 1] Opmerking: R2 heeft vaak het bereik (-inf, 1). De MSE kan groter zijn dan de waargenomen variantie, zodat R2 willekeurige grote negatieve waarden kan hebben, afhankelijk van de gegevens en de modelvoorspellingen. Geautomatiseerde ML-clips hebben R2-scores gerapporteerd op -1, dus een waarde van -1 voor R2 betekent waarschijnlijk dat de werkelijke R2-score kleiner is dan -1. Houd rekening met de andere metrische waarden en de eigenschappen van de gegevens bij het interpreteren van een negatieve R2-score .	Berekening
root_mean_squared_error	De wortel van de gemiddelde kwadratische fout (RMSE) is de vierkantswortel van het verwachte kwadratische verschil tussen het doel en de voorspelling. Voor een onbevoordeelde estimator is RMSE gelijk aan de standaarddeviatie. Doelstelling: Dichter bij 0 hoe beter Bereik: [0, inf) Typen: root_mean_squared_error normalized_root_mean_squared_error: de root_mean_squared_error gedeeld door het bereik van de gegevens.	Berekening
root_mean_squared_log_error	Wortelgemiddelde kwadratische logboekfout is de vierkantswortel van de verwachte logaritmische fout. Doelstelling: Dichter bij 0 hoe beter Bereik: [0, inf) Typen: root_mean_squared_log_error normalized_root_mean_squared_log_error: de root_mean_squared_log_error gedeeld door het bereik van de gegevens.	Berekening
spearman_correlation	Spearman correlatie is een niet-parametrische meting van de monotoniteit van de relatie tussen twee gegevenssets. In tegenstelling tot de Pearson-correlatie gaat de Spearman-correlatie er niet van uit dat beide gegevenssets normaal gesproken worden gedistribueerd. Net als bij andere correlatiecoëfficiënten varieert Spearman tussen -1 en 1, waarbij 0 geen correlatie impliceert. Correlaties van -1 of 1 impliceren een exacte monotone relatie. Spearman is een metrische rangordecorrelatie, wat betekent dat wijzigingen in voorspelde of werkelijke waarden het Spearman-resultaat niet wijzigen als ze de rangorde van voorspelde of werkelijke waarden niet wijzigen. Doelstelling: Dichter bij 1 hoe beter Bereik: [-1, 1]	Berekening

Metrische normalisatie

Met geautomatiseerde ML worden regressie- en prognosegegevens genormaliseerd, waardoor vergelijking mogelijk is tussen modellen die zijn getraind op gegevens met verschillende bereiken. Een model dat is getraind op een gegevens met een groter bereik, heeft een hogere fout dan hetzelfde model dat is getraind op gegevens met een kleiner bereik, tenzij die fout wordt genormaliseerd.

Hoewel er geen standaardmethode is voor het normaliseren van metrische foutgegevens, gebruikt geautomatiseerde ML de algemene benadering van het delen van de fout door het bereik van de gegevens: normalized_error = error / (y_max - y_min)

Notitie

Het gegevensbereik wordt niet opgeslagen met het model. Als u deductie uitvoert met hetzelfde model in een holdout-testset en y_min y_max deze kan veranderen op basis van de testgegevens en de genormaliseerde metrische gegevens mogelijk niet rechtstreeks worden gebruikt om de prestaties van het model te vergelijken met trainings- en testsets. U kunt de waarde van y_min en y_max van uw trainingsset doorgeven om de vergelijking eerlijk te maken.

Metrische gegevens voorspellen: normalisatie en aggregatie

Voor het berekenen van metrische gegevens voor de evaluatie van het voorspellingsmodel zijn enkele speciale overwegingen vereist wanneer de gegevens meerdere tijdreeksen bevatten. Er zijn twee natuurlijke opties voor het aggregeren van metrische gegevens over meerdere reeksen:

1. Een macro-gemiddelde waarbij de metrische evaluatiegegevens uit elke reeks gelijk zijn aan gewicht,
2. Een micro-gemiddelde waarbij metrische evaluatiegegevens voor elke voorspelling gelijk zijn aan gewicht.

Deze gevallen hebben directe analogieën met macro- en microgemiddelden in classificatie van meerdere klassen.

Het onderscheid tussen macro's en micromiddelden kan belangrijk zijn bij het selecteren van een primaire metriek voor modelselectie. Denk bijvoorbeeld aan een retailscenario waarin u de vraag naar een selectie consumentenproducten wilt voorspellen. Sommige producten verkopen op hogere volumes dan andere. Als u een microgemiddelde RMSE als primaire metriek kiest, is het mogelijk dat de items met een hoog volume het grootste deel van de modelleringsfout bijdragen en dus de metrische gegevens overheerst. Het algoritme voor modelselectie kan de voorkeur geven aan modellen met een hogere nauwkeurigheid op de items met een hoog volume dan op de items met een laag volume. Een genormaliseerde RMSE met een macrogemiddelde geeft daarentegen ongeveer evenveel gewicht aan de items met een hoog volume.

In de volgende tabel ziet u welke van de metrische prognosegegevens van AutoML gebruikmaken van macro's versus micromiddeling:

Macrogemiddelde	Microgemiddelde
normalized_mean_absolute_error, , , normalized_median_absolute_errornormalized_root_mean_squared_errornormalized_root_mean_squared_log_error	mean_absolute_error, , median_absolute_errorroot_mean_squared_error, root_mean_squared_log_error, , r2_score, , explained_variancespearman_correlationmean_absolute_percentage_error

Houd er rekening mee dat metrische macrogemiddelde metrische gegevens elke reeks afzonderlijk normaliseren. De genormaliseerde metrische gegevens uit elke reeks worden vervolgens gemiddeld berekend om het uiteindelijke resultaat te geven. De juiste keuze van macro's versus micro is afhankelijk van het bedrijfsscenario, maar we raden over het algemeen aan om deze te gebruiken normalized_root_mean_squared_error.

Residuen

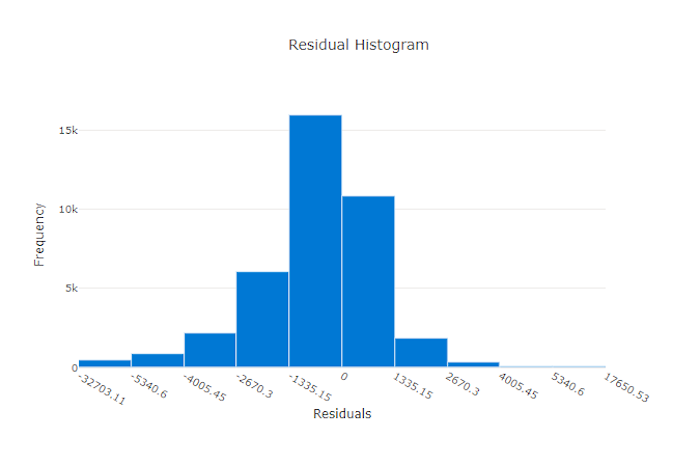
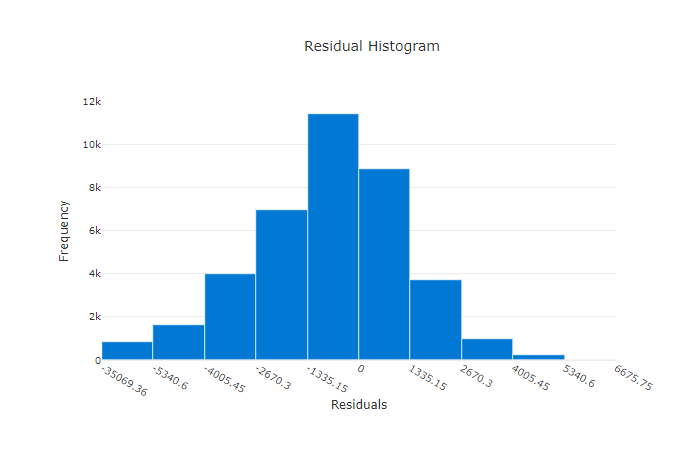
Het residuendiagram is een histogram van de voorspellingsfouten (residuen) die zijn gegenereerd voor regressie- en voorspellingsexperimenten. Residuen worden berekend zoals y_predicted - y_true voor alle steekproeven en worden vervolgens weergegeven als een histogram om modelvooroordelen weer te geven.

In dit voorbeeld zijn beide modellen enigszins vertekend om lager te voorspellen dan de werkelijke waarde. Dit is niet ongebruikelijk voor een gegevensset met een scheve verdeling van werkelijke doelen, maar geeft slechtere modelprestaties aan. Een goed model heeft een restverdeling die piekt op nul met weinig residuen bij de extremen. Een slechter model heeft een verspreide verdeling van residuen met minder monsters rond nul.

Residugrafiek voor een goed model

Residugrafiek voor een slecht model

Voorspeld versus waar

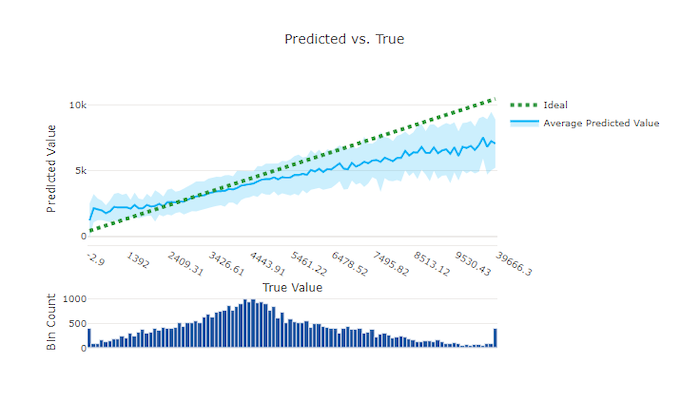
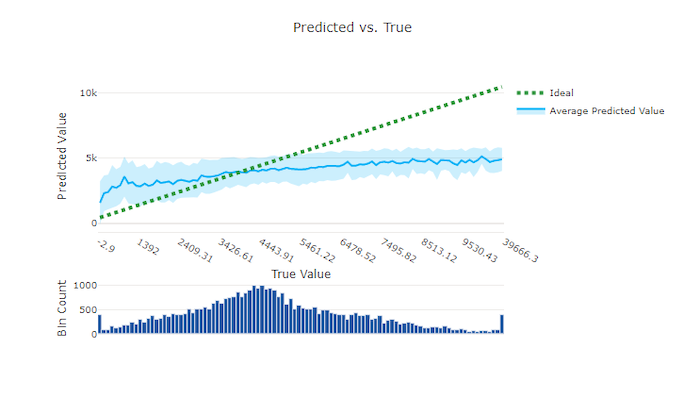
Voor regressie- en voorspellingsexperimenten wordt de relatie tussen de doelfunctie (waar/werkelijke waarden) en de voorspellingen van het model uitgezet. De werkelijke waarden worden op de x-as geplaatst en voor elke bin wordt de gemiddelde voorspelde waarde weergegeven met foutbalken. Hiermee kunt u zien of een model bevooroordeeld is om bepaalde waarden te voorspellen. De lijn geeft de gemiddelde voorspelling weer en het gearceerde gebied geeft de variantie van voorspellingen rond dat gemiddelde aan.

Vaak heeft de meest voorkomende werkelijke waarde de meest nauwkeurige voorspellingen met de laagste variantie. De afstand van de trendlijn van de ideale y = x lijn waarbij er weinig werkelijke waarden zijn, is een goede maat voor modelprestaties bij uitbijters. U kunt het histogram onderaan de grafiek gebruiken om te redeneren over de werkelijke gegevensdistributie. Door meer gegevensvoorbeelden op te nemen waarbij de distributie sparse is, kunnen de modelprestaties op ongelezen gegevens worden verbeterd.

In dit voorbeeld ziet u dat het betere model een voorspelde versus werkelijke lijn heeft die dichter bij de ideale y = x lijn ligt.

Voorspeld versus waar diagram voor een goed model

Voorspeld versus waar diagram voor een slecht model

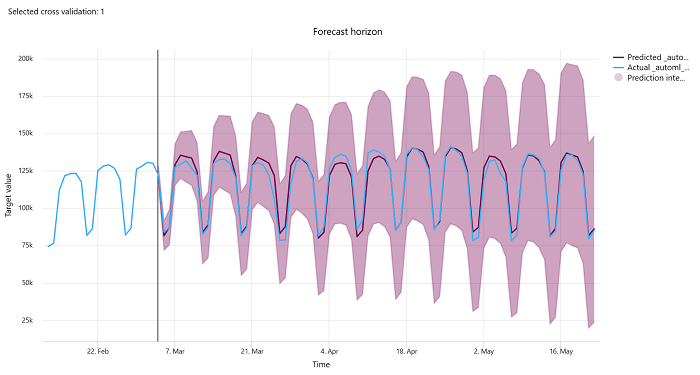
Prognosehorizk

Voor voorspellingsexperimenten plot het diagram met de prognose horizon de relatie tussen de voorspelde waarde van de modellen en de werkelijke waarden die in de loop van de tijd zijn toegewezen per kruisvalidatievouw, tot vijf vouwen. De x-as wijst de tijd toe op basis van de frequentie die u tijdens het instellen van de training hebt opgegeven. De verticale lijn in het diagram markeert het prognose-horizonpunt ook wel de horizonlijn genoemd. Dit is de tijdsperiode waarop u voorspellingen wilt gaan genereren. Links van de lijn van de prognose horizon kunt u historische trainingsgegevens bekijken om eerdere trends beter te visualiseren. Rechts van de prognose horizon kunt u de voorspellingen (de paarse lijn) visualiseren ten opzichte van de werkelijke waarden (de blauwe lijn) voor de verschillende kruisvalidatievouwen en tijdreeks-id's. Het gearceerde paarse gebied geeft de betrouwbaarheidsintervallen of variantie van voorspellingen rond dat gemiddelde aan.

U kunt kiezen welke combinaties van kruisvalidatievouw en tijdreeks-id moeten worden weergegeven door op het bewerkte potloodpictogram in de rechterbovenhoek van de grafiek te klikken. Selecteer uit de eerste vijf kruisvalidatievouwen en maximaal 20 verschillende tijdreeks-id's om de grafiek voor uw verschillende tijdreeksen te visualiseren.

Belangrijk

Deze grafiek is beschikbaar in de trainingsuitvoering voor modellen die zijn gegenereerd op basis van trainings- en validatiegegevens, evenals in de testuitvoering op basis van trainingsgegevens en testgegevens. We staan maximaal 20 gegevenspunten toe vóór en maximaal 80 gegevenspunten na de oorsprong van de prognose. Voor DNN-modellen toont deze grafiek in de trainingsuitvoering gegevens uit het laatste tijdvak, d.w. nadat het model volledig is getraind. Deze grafiek in de testuitvoering kan een tussenruimte hebben vóór de horizonlijn als er tijdens de trainingsuitvoering expliciet validatiegegevens zijn opgegeven. Dit komt doordat trainingsgegevens en testgegevens worden gebruikt in de testuitvoering, waarbij de validatiegegevens worden weggelaten die leiden tot een hiaat.

Metrische gegevens voor afbeeldingsmodellen (preview)

Geautomatiseerde ML gebruikt de afbeeldingen uit de validatiegegevensset voor het evalueren van de prestaties van het model. De prestaties van het model worden gemeten op epoch-niveau om te begrijpen hoe de training vordert. Er wordt een periode verstreken wanneer een volledige gegevensset precies eenmaal wordt doorgestuurd en achteruit wordt doorgegeven via het neurale netwerk.

Metrische gegevens voor afbeeldingsclassificatie

De primaire metriek voor evaluatie is nauwkeurigheid voor binaire en classificatiemodellen met meerdere klassen en IoU (Intersection over Union) voor classificatiemodellen met meerdere labels. De metrische classificatiegegevens voor afbeeldingsclassificatiemodellen zijn hetzelfde als de classificatiemodellen die zijn gedefinieerd in de sectie metrische classificatiegegevens . De verlieswaarden die aan een epoch zijn gekoppeld, worden ook geregistreerd die kunnen helpen bij het controleren van de voortgang van de training en bepalen of het model overfitting of onderbehorend is.

Elke voorspelling van een classificatiemodel is gekoppeld aan een betrouwbaarheidsscore, wat het betrouwbaarheidsniveau aangeeft waarmee de voorspelling is gedaan. Classificatiemodellen met meerdere labels worden standaard geëvalueerd met een scoredrempel van 0,5, wat betekent dat alleen voorspellingen met ten minste dit betrouwbaarheidsniveau als een positieve voorspelling voor de bijbehorende klasse worden beschouwd. Classificatie met meerdere klassen maakt geen gebruik van een scoredrempel, maar in plaats daarvan wordt de klasse met de maximale betrouwbaarheidsscore beschouwd als de voorspelling.

Metrische gegevens op epoch-niveau voor afbeeldingsclassificatie

In tegenstelling tot de classificatiegegevens voor tabellaire gegevenssets, registreren afbeeldingsclassificatiemodellen alle metrische classificatiegegevens op epoch-niveau, zoals hieronder wordt weergegeven.

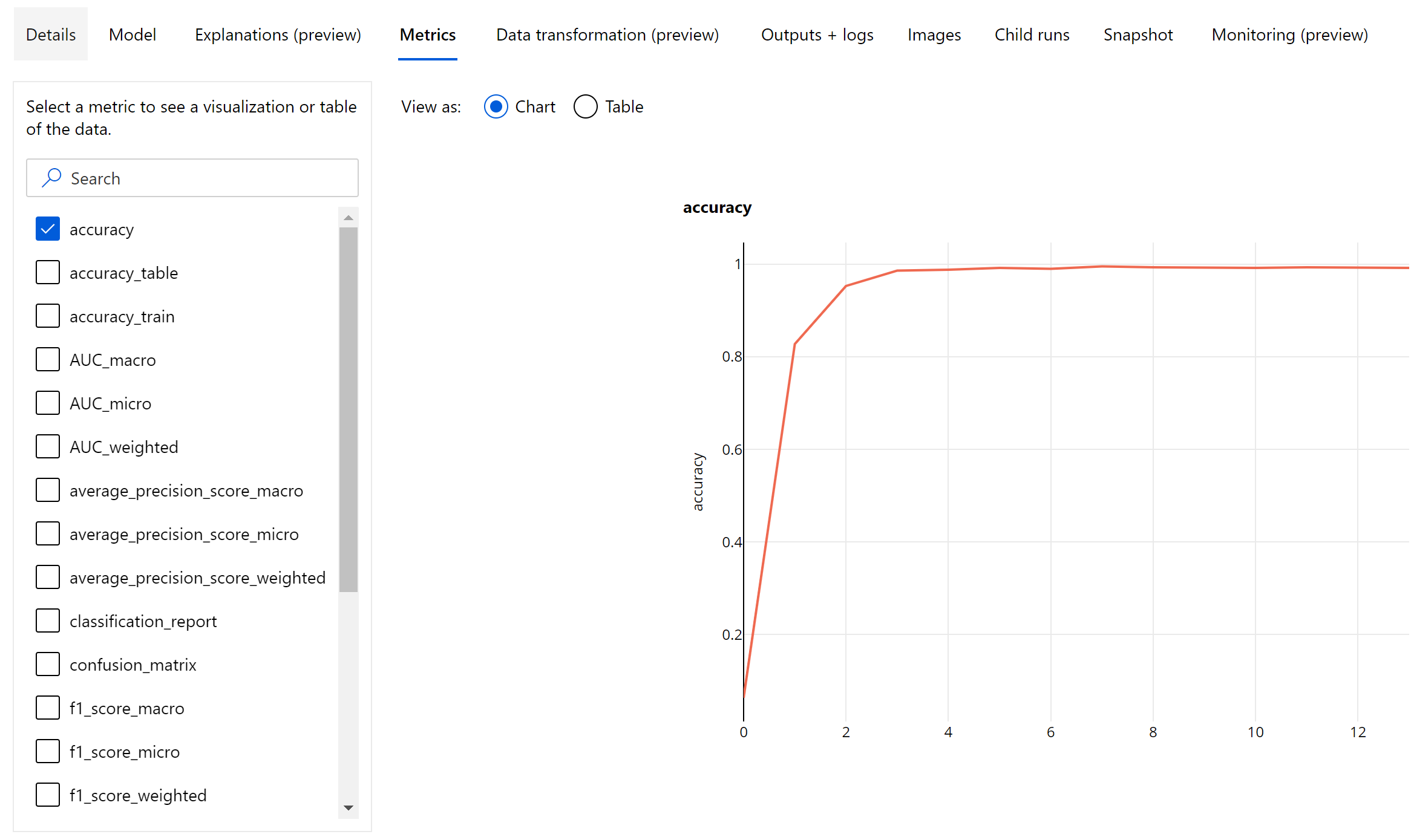
Samenvatting metrische gegevens voor afbeeldingsclassificatie

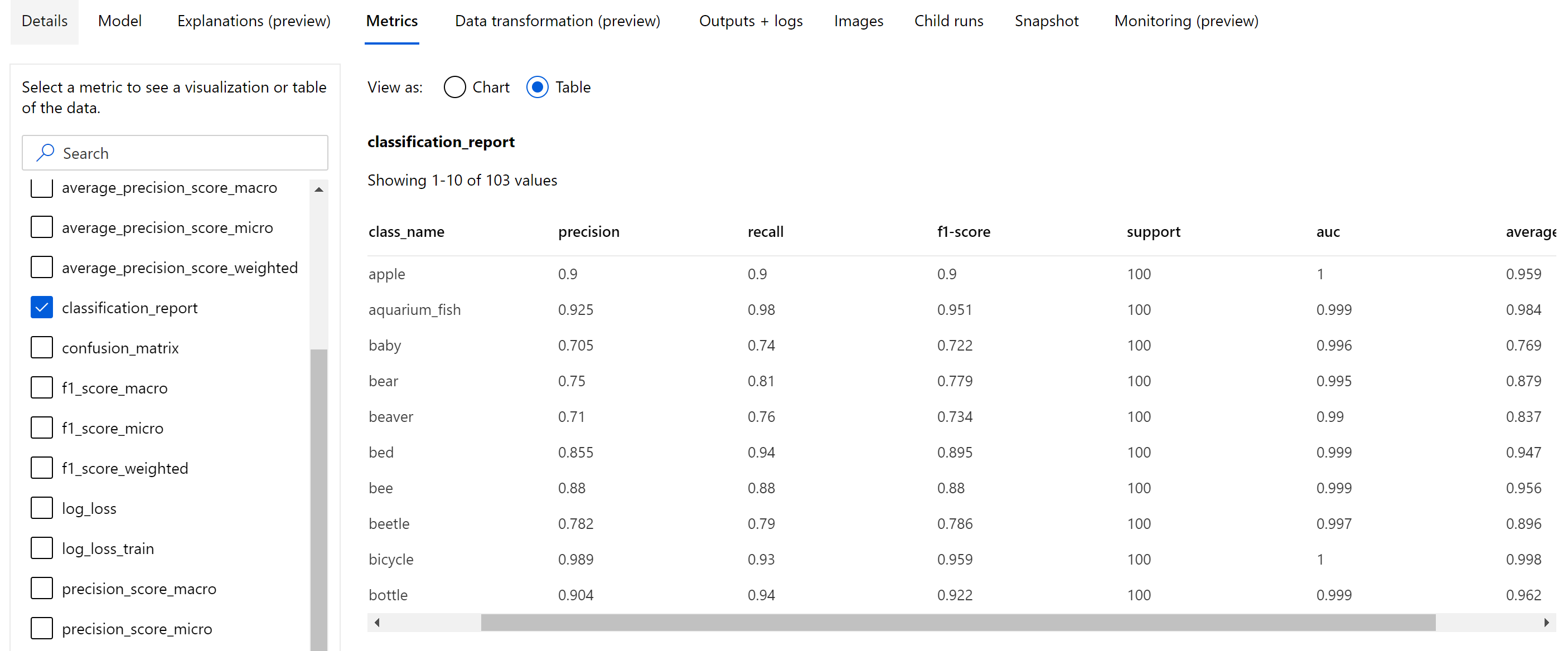
Afgezien van de scalaire metrische gegevens die zijn vastgelegd op epoch-niveau, registreren afbeeldingsclassificatiemodel ook samenvattingsstatistieken zoals verwarringsmatrix, classificatiegrafieken, waaronder ROC-curve, precisie-relevante curve en classificatierapport voor het model uit het beste tijdvak waar we de hoogste primaire metrische score (nauwkeurigheid) krijgen.

Classificatierapport biedt de waarden op klasseniveau voor metrische gegevens, zoals precisie, relevante overeenkomsten, f1-score, ondersteuning, auc en average_precision met verschillende niveaus van gemiddelde- micro, macro en gewogen, zoals hieronder wordt weergegeven. Raadpleeg de definities van metrische gegevens uit de sectie metrische classificatiegegevens .

Metrische gegevens over objectdetectie en instantiesegmentatie

Elke voorspelling van een afbeeldingsobjectdetectie of exemplaarsegmentatiemodel is gekoppeld aan een betrouwbaarheidsscore. De voorspellingen met een betrouwbaarheidsscore die groter zijn dan de scoredrempel zijn uitvoer als voorspellingen en worden gebruikt in de metrische berekening, waarvan de standaardwaarde specifiek is voor het model en waarnaar kan worden verwezen vanaf de pagina hyperparameterafstemming (box_score_threshold hyperparameter).

De metrische berekening van een afbeeldingsobjectdetectie- en exemplaarsegmentatiemodel is gebaseerd op een overlappingsmeting die is gedefinieerd door een metrische waarde genaamd IoU (Intersection over Union), die wordt berekend door het overlapgebied tussen de grondwaar en de voorspellingen te delen door het gebied van samenvoeging van de grondwaar en de voorspellingen. De IoU die wordt berekend op basis van elke voorspelling wordt vergeleken met een overlappingsdrempel die een IoU-drempelwaarde wordt genoemd, waarmee wordt bepaald hoeveel een voorspelling moet overlappen met een door de gebruiker geannoteerde grondwaar om als een positieve voorspelling te worden beschouwd. Als de IoU die is berekend op basis van de voorspelling kleiner is dan de overlappingsdrempel, wordt de voorspelling niet beschouwd als een positieve voorspelling voor de bijbehorende klasse.

De primaire metriek voor de evaluatie van afbeeldingsobjectdetectie- en instantiesegmentatiemodellen is de gemiddelde gemiddelde precisie (mAP). De mAP is de gemiddelde waarde van de gemiddelde precisie (AP) in alle klassen. Geautomatiseerde ML-objectdetectiemodellen ondersteunen de berekening van mAP met behulp van de onderstaande twee populaire methoden.

Metrische gegevens van Pascal VOC:

Pascal VOC mAP is de standaardwijze van mAP-berekeningen voor objectdetectie-/exemplaarsegmentatiemodellen. De mAP-methode pascal VOC berekent het gebied onder een versie van de precisie-relevante curve. Eerste p(ri), dat precisie bij relevante overeenkomsten is, wordt berekend voor alle unieke relevante waarden. p(ri) wordt vervolgens vervangen door maximale precisie verkregen voor elke relevante r' >= ri. De precisiewaarde neemt monotonisch af in deze versie van de curve. Pascal VOC mAP meetwaarde wordt standaard geëvalueerd met een IoU-drempelwaarde van 0,5. In deze blog vindt u een gedetailleerde uitleg van dit concept.

COCO-metrische gegevens:

De COCO-evaluatiemethode maakt gebruik van een geïnterpoleerde methode van 101 punten voor AP-berekening, samen met gemiddelden van meer dan tien IoU-drempelwaarden. AP@[.5:.95] komt overeen met het gemiddelde AP voor IoU van 0,5 tot 0,95 met een stapgrootte van 0,05. Geautomatiseerde ML registreert alle 12 metrische gegevens die zijn gedefinieerd door de COCO-methode, inclusief de AP en AR(gemiddelde relevante overeenkomsten) op verschillende schaalaanpassingen in de toepassingslogboeken, terwijl in de gebruikersinterface voor metrische gegevens alleen de mAP met een IoU-drempelwaarde van 0,5 wordt weergegeven.

Tip

De evaluatie van het afbeeldingsobjectdetectiemodel kan coco-metrische gegevens gebruiken als de validation_metric_type hyperparameter is ingesteld op 'coco' zoals uitgelegd in de sectie hyperparameterafstemming .

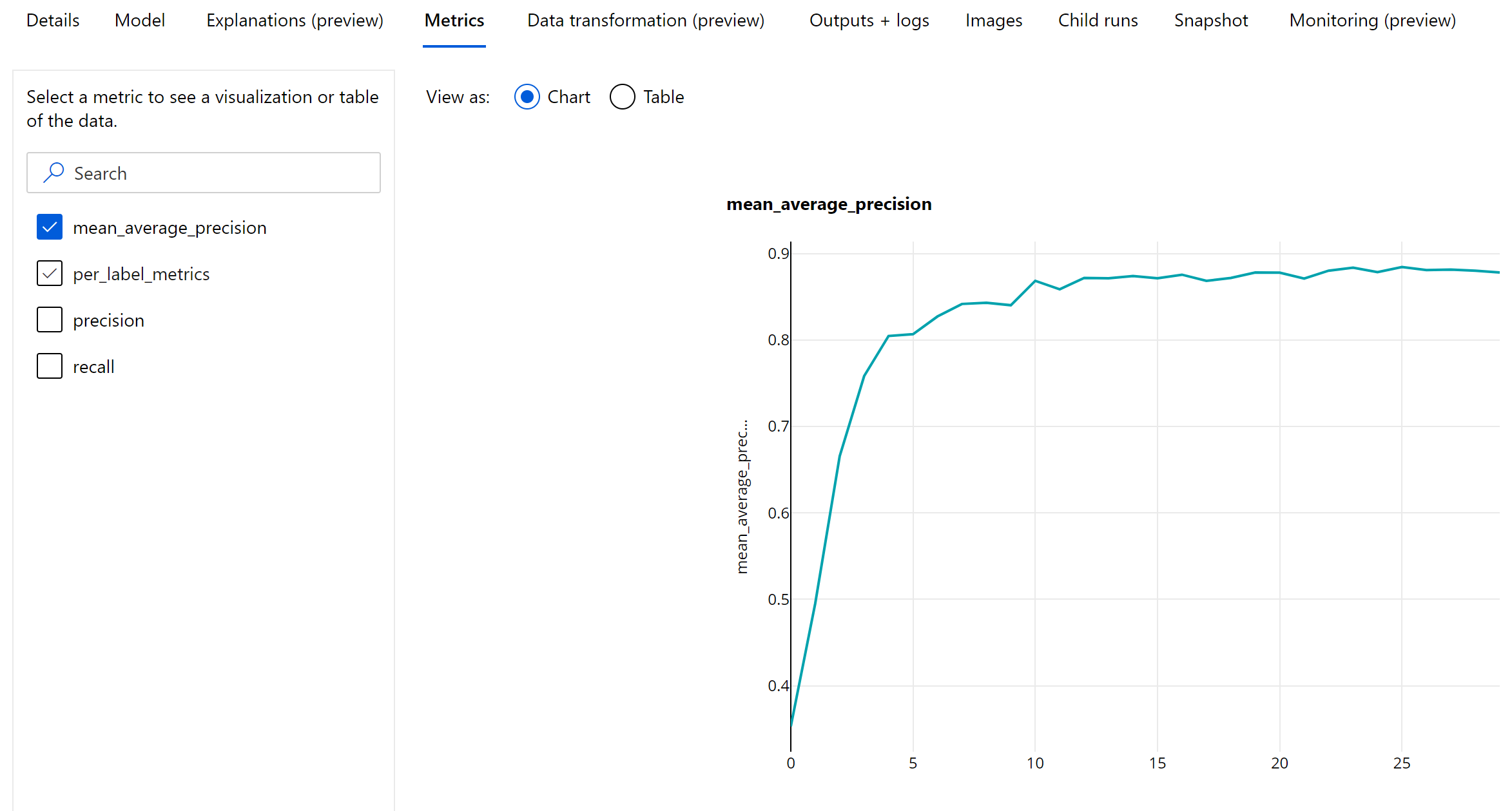
Metrische gegevens op epoch-niveau voor objectdetectie en exemplaarsegmentatie

De mAP-, precisie- en relevante waarden worden vastgelegd op epoch-niveau voor afbeeldingsobjectdetectie-/exemplaarsegmentatiemodellen. De metrische gegevens mAP, precisie en relevante overeenkomsten worden ook geregistreerd op klasseniveau met de naam 'per_label_metrics'. De per_label_metrics moet worden weergegeven als een tabel.

Notitie

Metrische gegevens op epoch-niveau voor precisie, relevante overeenkomsten en per_label_metrics zijn niet beschikbaar bij gebruik van de 'coco'-methode.

Verantwoordelijk AI-dashboard voor het best aanbevolen AutoML-model (preview)

Het Azure Machine Learning Responsible AI-dashboard biedt één interface waarmee u verantwoorde AI in de praktijk effectief en efficiënt kunt implementeren. Verantwoordelijk AI-dashboard wordt alleen ondersteund met behulp van tabelgegevens en wordt alleen ondersteund voor classificatie- en regressiemodellen. Het brengt verschillende volwassen verantwoordelijke AI-hulpprogramma's samen op het gebied van:

• Modelprestatie- en billijkheidsevaluatie
• Gegevens verkennen
• Interpreteerbaarheid van machine learning
• Foutenanalyse

Hoewel metrische gegevens en grafieken voor modelevaluatie goed zijn voor het meten van de algemene kwaliteit van een model, zijn bewerkingen zoals het inspecteren van de redelijkheid van het model, het bekijken van de uitleg (ook wel bekend als welke gegevensset een model bevat dat wordt gebruikt om de voorspellingen te doen), het inspecteren van de fouten en potentiële blinde vlekken essentieel bij het oefenen van verantwoorde AI. Daarom biedt geautomatiseerde ML een verantwoordelijk AI-dashboard waarmee u verschillende inzichten voor uw model kunt observeren. Zie hoe u het dashboard voor verantwoorde AI in de Azure Machine Learning-studio kunt bekijken.

Bekijk hoe u dit dashboard kunt genereren via de gebruikersinterface of de SDK.

Modeluitleg en functiebelangen

Hoewel metrische gegevens en grafieken voor modelevaluatie goed zijn voor het meten van de algemene kwaliteit van een model, is het controleren van welke gegevenssets een model gebruikt om voorspellingen te doen essentieel bij het oefenen van verantwoorde AI. Daarom biedt geautomatiseerde ML een dashboard voor modeluitleg om de relatieve bijdragen van gegevenssetfuncties te meten en te rapporteren. Bekijk hoe u het dashboard uitleg in de Azure Machine Learning-studio kunt bekijken.

Notitie

Interpreteerbaarheid, beste modeluitleg, is niet beschikbaar voor geautomatiseerde ML-voorspellingsexperimenten die de volgende algoritmen aanbevelen als het beste model of ensemble:

• TCNForecaster
• AutoArima
• ExponentialSmoothing
• Profeet
• Gemiddeld
• Naïef
• Seizoensgemiddelde
• Seizoen naïef

Volgende stappen

• Probeer de voorbeeldnotebooks van het geautomatiseerde machine learning-model uit.
• Voor geautomatiseerde ML-specifieke vragen kunt u contact opnemen met askautomatedml@microsoft.com.