Notitie
Voor toegang tot deze pagina is autorisatie vereist. U kunt proberen u aan te melden of de directory te wijzigen.
Voor toegang tot deze pagina is autorisatie vereist. U kunt proberen de mappen te wijzigen.
Net zoals bits het fundamentele object van informatie in klassieke computing zijn, zijn qubits (kwantumbits ) het fundamentele object van informatie in kwantumcomputing. Om deze correspondentie te begrijpen, bekijkt dit artikel het eenvoudigste voorbeeld: één qubit.
Weergave van een qubit
Hoewel een bit, of binair cijfer, een waarde 0 of 1 kan hebben, kan een qubit een waarde hebben die 0$, $1$ of een kwantumsuperpositie van $0$ en $1$ is$.$$$$
De toestand van één qubit kan worden beschreven door een tweedimensionale kolomvector van eenheidsnorm, dat wil zeggen, de grootte van de waarden moet worden opgeteld tot $1$. Deze vector, de kwantumstatusvector genoemd, bevat alle informatie die nodig is om het kwantumsysteem met één qubit te beschrijven, net zoals één bit alle informatie bevat die nodig is om de status van een binaire variabele te beschrijven. Zie Vector en matrices voor de basisprincipes van vectoren en matrices in kwantumcomputing.
Elke tweedimensionale kolomvector van reële of complexe getallen met norm $1$ vertegenwoordigt een mogelijke kwantumtoestand die wordt bewaard door een qubit. Vertegenwoordigt dus $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$een qubitstatus als $\alpha$ en $\beta$ complexe getallen zijn die voldoen aan $|\alpha|^2 + |\beta|^2 = 1.$
Enkele voorbeelden van geldige kwantumstatusvectoren die qubits vertegenwoordigen, zijn $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ en $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Deze twee vectoren vormen een basis voor de vectorruimte die de toestand van de qubit beschrijft. Dit betekent dat elke kwantumstatusvector kan worden geschreven als een som van deze basisvectoren. Specifiek kunnen de vector $\begin{bmatrix} x \\ y \end{bmatrix}$ worden geschreven als $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Hoewel elke rotatie van deze vectoren als een perfect geldige basis voor de qubit zou dienen, wordt deze specifieke gekozen door deze de rekenkundige basis aan te roepen.
Deze twee kwantumtoestanden komen overeen met de twee toestanden van een klassieke bit, namelijk $0$ en $1$. De standaardconventie is om te kiezen
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$$1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
hoewel de tegenovergestelde keuze even goed kan worden genomen. Uit het oneindige aantal mogelijke kwantumtoestandsvectoren met één qubit komen dus slechts twee overeen met toestanden van klassieke bits; niet alle andere kwantumtoestanden.
Een qubit meten
Hoe een qubit te vertegenwoordigen die wordt uitgelegd, kan men enige intuïtiefheid krijgen voor wat deze toestanden vertegenwoordigen door het concept van meting te bespreken. Een meting komt overeen met het informele idee van 'kijken' naar een qubit, waarmee de kwantumtoestand onmiddellijk wordt samengevouwen tot een van de twee klassieke toestanden $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ of $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Wanneer een qubit wordt gegeven door de kwantumtoestandvector $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ en gemeten, wordt het resultaat $0$ verkregen met kans $|\alpha|^2$ en het resultaat $1$ met kans $|\beta|^2$. Bij resultaat $0$ is $\begin{bmatrix} de nieuwe toestand van de qubit 1 \\ 0 \end{bmatrix}$; op resultaat $1$ is $\begin{bmatrix} de status 0 \\ 1 \end{bmatrix}$. Houd er rekening mee dat deze waarschijnlijkheden maximaal $1$ bedragen vanwege de normalisatievoorwaarde $|\alpha|^2 + |\beta|^2 = 1$.
De eigenschappen van de meting betekenen ook dat het algehele teken van de kwantumstatusvector niet relevant is. Het negeren van een vector is gelijk aan $\alpha\rightpijl -\alpha$ en $\beta\rightpijl -\beta$. Omdat de waarschijnlijkheid van het meten van $0$ en $1$ afhankelijk is van het kwadraat van de grootte van de termen, verandert het invoegen van dergelijke tekens de waarschijnlijkheden totaal niet. Dergelijke fasen worden vaak genoemd "globale fasen" en over het algemeen kan van de vorm $e^{i \phi}$ zijn in plaats van alleen $\pm 1$.
Een laatste belangrijke eigenschap van meting is dat het niet noodzakelijkerwijs alle kwantumtoestandsvectoren beschamen. Als één begint met een qubit in de toestand $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, die overeenkomt met de klassieke toestand $0$, resulteert het meten van deze toestand altijd in het resultaat $0$ en blijft de kwantumstatus ongewijzigd. In dit opzicht, als er alleen klassieke bits zijn (bijvoorbeeld qubits die ofwel $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ of $\begin{bmatrix}0 \\ 1 \end{bmatrix}$) zijn, kan meting het systeem niet beschadigen. Dit betekent dat klassieke gegevens kunnen worden gerepliceerd en bewerkt op een kwantumcomputer, net zoals op een klassieke computer. De mogelijkheid om gegevens in beide toestanden tegelijk op te slaan, is echter wat kwantumcomputing verheft boven wat mogelijk is klassiek en verder berooft kwantumcomputers van de mogelijkheid om kwantumgegevens ongediscriminaliseerd te kopiëren, zie ook de no-clone theorem.
Qubits en transformaties visualiseren met behulp van de Bloch sphere
Qubits kunnen ook in 3D worden afgebeeld met behulp van de Bloch-sfeer representatie. De Bloch sphere biedt een manier om een kwantumtoestand met één qubit (een tweedimensionale complexe vector) te beschrijven als een driedimensionale reële vector. Dit is belangrijk omdat het ons in staat stelt om statussen met één qubit te visualiseren en daardoor redeneringen te ontwikkelen die waardevol kunnen zijn bij het begrijpen van multi-qubitstatussen (waarbij de Bloch sphere-representatie helaas afbreekt). De Bloch bol kan als volgt worden gevisualiseerd:
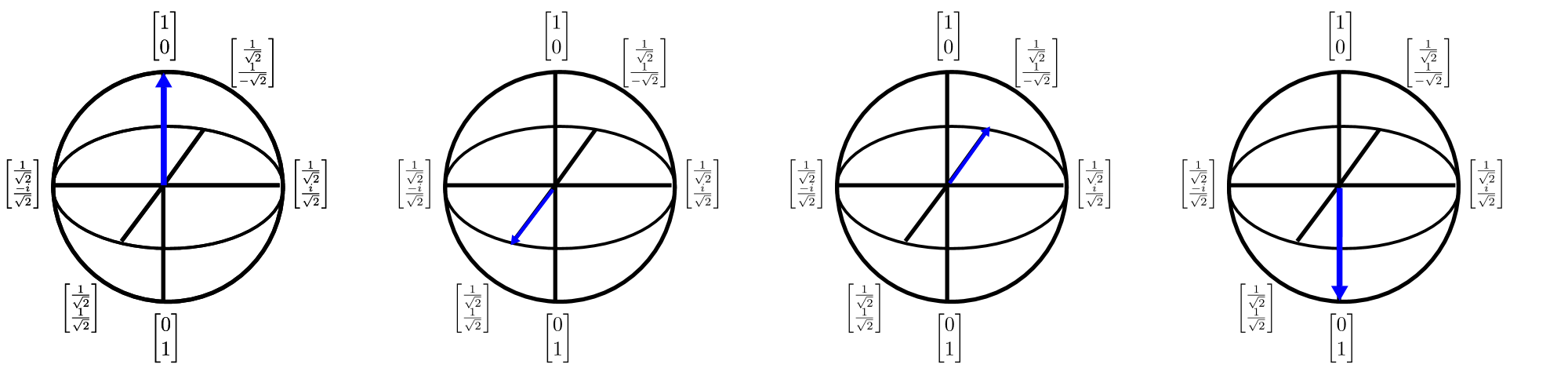
De pijlen in dit diagram geven de richting aan waarin de kwantumstatusvector wijst en elke transformatie van de pijl kan worden beschouwd als een draaiing over een van de kardinaliteitsassen. Hoewel het denken over een kwantumberekening als een reeks rotaties een krachtige intuïtieve kennis is, is het lastig om deze intuïtieve methode te gebruiken om algoritmen te ontwerpen en te beschrijven. Q# vermindert dit probleem door een taal op te geven voor het beschrijven van dergelijke rotaties.
Bewerkingen met één qubit
Kwantumcomputers verwerken gegevens door een universele set kwantumpoorten toe te passen die elke rotatie van de kwantumstatusvector kunnen emuleren. Dit begrip van universaliteit is vergelijkbaar met het begrip universaliteit voor traditionele (bijvoorbeeld klassieke) computing waarbij een poortset als universeel wordt beschouwd als elke transformatie van de invoerbits kan worden uitgevoerd met behulp van een eindig lengtecircuit. In kwantumcomputing zijn de geldige transformaties die we mogen uitvoeren op een qubit unitaire transformaties en metingen. De toegevoegde bewerking of het complex geconjugeerde transponeren is van cruciaal belang voor quantum computing, omdat het nodig is om kwantumtransformaties te omkeren.
Bewerkingen met één qubit of kwantumpoorten met één qubit kunnen worden geclassificeerd in twee categorieën: Clifford-poorten en de niet-Clifford-poorten. Niet-Clifford poorten bestaan alleen uit de T-poort (ook wel de \pi/8-poort genoemd).
$$ T=\begin{bmatrix} 1 & 0 \ 0 & e^{i\pi/4}\end{bmatrix}. $$
De standaardset single-qubit Clifford-poorten, die standaard zijn opgenomen in Q#, bevatten
$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \ 1& 0 \end{bmatrix}= HT^4H, $$
$$ Y =\begin{bmatrix} 0 & -i \ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\ 0&-1 \end{bmatrix}=T^4. $$
Hier worden de bewerkingen $X$, $Y$ en $Z$ vooral vaak gebruikt en worden Pauli-operators genoemd na hun maker Wolfgang Pauli. Samen met de niet-Clifford-poort (de $T-gate$) kunnen deze bewerkingen worden samengesteld om elke unitaire transformatie op één qubit te benaderen.
Hoewel de vorige de populairste primitieve poorten vormen voor het beschrijven van bewerkingen op het logische niveau van de stack (denk aan het logische niveau als het niveau van het kwantumalgoritmen), is het vaak handig om minder eenvoudige bewerkingen op algoritmeniveau te overwegen, bijvoorbeeld bewerkingen dichter bij een functiebeschrijvingsniveau. Gelukkig zijn er ook methoden beschikbaar voor het implementeren van unitairs op hoger niveau, waardoor algoritmen op hoog niveau kunnen worden geïmplementeerd zonder alles expliciet te ontleden naar Clifford- en T-gates.
De eenvoudigste primitieve is de enkele qubit-rotatie. Er worden doorgaans drie draaiingen met één qubit beschouwd: $R_x$, $R_y$ en $R_z$. Als u de actie van de draaiing $R_x(\theta)$ wilt visualiseren, kunt u zich bijvoorbeeld voorstellen dat u uw rechtervinger langs de richting van de $x-as$ van de Bloch-bol wijst en de vector met uw hand draait door een hoek van $\theta/2$ radialen. Deze verwarrende factor van $2$ komt voort uit het feit dat orthogonale vectoren $180^\circ$ apart zijn wanneer ze zijn uitgezet op de Bloch-bol, maar eigenlijk $90^\circ$ graden van elkaar liggen geometrisch. De bijbehorende unitaire matrices zijn:
$$ \begin{align*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& 0\\ 0& e^{i\theta/2}\end{bmatrix}, \\& R_x(\theta) = e^{-i\theta X/2}= HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& R_y(\theta) = e^{-i\theta Y/2}= SHR_z(\theta)HS^\dagger=\begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}. \end{uitlijnen*}$$
Net zoals elke drie draaiingen samen kunnen worden gecombineerd om een willekeurige draaiing in drie dimensies uit te voeren, is het te zien in de weergave van de Bloch-bol dat elke unitaire matrix ook kan worden geschreven als een reeks van drie draaiingen. In het bijzonder geldt dat er voor elke unitair matrix $U$$\alpha,\beta,\gamma,\delta$ bestaan zodanig dat $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Zo vormen $R_z(\theta)$ en $H$ ook een universele poortset, hoewel het geen discrete set is, omdat $\theta$ elke waarde kan aannemen. Daarom zijn dergelijke continue poorten cruciaal voor kwantumberekeningen, met name op het ontwerpniveau van het kwantumalgoritmen. Om een fouttolerante hardware-implementatie te bereiken, zullen ze uiteindelijk worden gecompileerd in discrete poortreeksen die deze rotaties nauwkeurig nabootsen.