What is entanglement?
Entanglement is one of the key features of quantum mechanics that distinguishes it from classical mechanics.
But what is entanglement? How does it work? And why is it so important for quantum information?
Understanding quantum entanglement
Imagine that you have two qubits, $A$ and $B$. The qubits are independent from each other, which means that the information about the state of qubit $A$, whatever it is, belongs only to qubit $A$. Similarly the information about the state of qubit $B$ belongs to qubit $B$. You can describe the state of each qubit. In this case, the qubits are not entangled, because they aren't sharing any information.
Now imagine that you entangle the qubits (you'll learn how to do this later). If qubits $A$ and $B$ are entangled, then the information about the state of qubit $A$ is not independent of the state of qubit $B$. When entangled, information is shared between both qubits, and there's no way to infer the state of qubit $A$ or state of qubit $B$. You can only describe the state of the global system, not the state of the individual qubits.
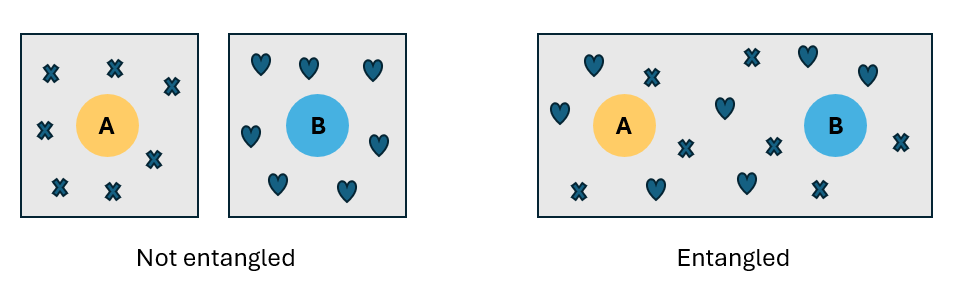
Entanglement is a quantum correlation between two or more particles. If two particles are entangled, they cannot be described independently, but only as a whole system.
Describing quantum entanglement
Imagine two qubits $A$ and $B$ such that the state of the global system $\ket{\phi}$ is:
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
Note
In Dirac notation, $\ket{0_A 0_B}= |0\rangle_\text{A} |0\rangle_\text{B}$. The first position corresponds to the first qubit, and the second position corresponds to the second qubit.
The global system $\ket{\phi}$ is in a superposition of the states $|00\rangle$ and $|11\rangle$. If you measure both qubits, only two outcomes are possible: $\ket{00}$ and $\ket{11}$, and each has the same probability of $\frac{1}{2}$.
But what is the individual state of qubit $A$? And of qubit $B$? If you try to describe the state of qubit $A$ without considering the state of qubit $B$, you would fail. Subsystems $A$ and $B$ are entangled, which means that they are correlated, and cannot be described independently.
Tip
If you're familiar with algebra and Dirac notation, a good exercise is to try to modify the $\ket{\phi}$ state to get something like the state of qubit $A$ times the state of qubit $B$. If you try to expand the parenthesis, get the common factor, etc, you'll see that it's not possible.
The quantum state $\ket{\phi}$ is a special entangled state, called Bell state. There are four Bell states.
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{00} + \frac1{\sqrt2}\ket{11}$$ $$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11} $$ $$ \ket{\psi^{+}}=\frac1{\sqrt2}\ket{01} + \frac1{\sqrt2}\ket{10} $$ $$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1{\sqrt2}\ket{10} $$
Using entanglement as a resource
At this point, you might be wondering what's the big deal about entanglement?
When two particles are entangled, subsystems are correlated and cannot be described independently. But here's the interesting part: the measurement outcomes are also correlated. That is, whatever operation happens to the state of one qubit in an entangled pair, also affects to the state of the other qubit.
For example, consider the $\ket{\phi^{+}}$ state,
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{00} + \frac1{\sqrt2}\ket{11}$$
If you measure both qubits, you get either $|00\rangle$ or $|11\rangle$ with equal probability. There's zero probability of obtaining the states $|01\rangle$ and $|10\rangle$.
But what happens if you measure only one qubit?
If you measure only the qubit $A$ and you get the $|0\rangle$ state, this means that the global system collapses to the state $\ket{00}$. This is the only possible outcome, since the probability of measuring $|01\rangle$ is zero.
Therefore, without measuring the qubit $B$ you can be positive that the second qubit is also in $|0\rangle$ state. The measurement outcomes are correlated because the qubits are entangled.
Entanglement can exist between two particles even if they are separated by large distances. This correlation is stronger than any classical correlation, and it is a key resource for quantum information processing tasks such as quantum teleportation, quantum cryptography, and quantum computing.