Função D3DXSHEvalHemisphereLight (D3dx9math.h)

Observação

A biblioteca de utilitários D3DX (D3DX 9, D3DX 10 e D3DX 11) foi preterida e não tem suporte para aplicativos da Windows Store.

Observação

Em vez de usar essa função, recomendamos que você use a função de biblioteca Spherical Harmonics MathXMSHEvalHemisphereLight.

Avalia uma luz que é uma interpolação linear entre duas cores sobre a esfera.

Sintaxe

HRESULT D3DXSHEvalHemisphereLight(
  _In_       UINT        Order,
  _In_ const D3DXVECTOR3 *pDir,
  _In_       D3DXCOLOR   Top,
  _In_       D3DXCOLOR   Bottom,
  _In_       FLOAT       *pROut,
  _In_       FLOAT       *pGOut,
  _In_       FLOAT       *pBOut
);

Parâmetros

Order [in]

Tipo: UINT

Ordem da avaliação harmônica esférica (SH). Deve estar no intervalo de D3DXSH_MINORDER para D3DXSH_MAXORDER, inclusive. A avaliação gera coeficientes Order². O grau da avaliação é Order - 1.

pDir [in]

Tipo: const D3DXVECTOR3*

Ponteiro para o vetor de direção do eixo do hemisfério (x, y, z) no qual avaliar as funções de base SH. Consulte Observações.

Superior [in]

Tipo: D3DXCOLOR

A cor do céu.

Inferior [in]

Tipo: D3DXCOLOR

A cor do solo.

pROut [in]

Tipo: FLOAT*

Ponteiro para o vetor SH de saída para o componente vermelho.

pGOut [in]

Tipo: FLOAT*

Ponteiro para o vetor SH de saída para o componente verde.

pBOut [in]

Tipo: FLOAT*

Ponteiro para o vetor SH de saída para o componente azul.

Valor retornado

Tipo: HRESULT

Se a função for bem-sucedida, o valor retornado será D3D_OK. Se a função falhar, o valor retornado poderá ser: D3DERR_INVALIDCALL.

Comentários

A interpolação é feita linearmente entre os dois pontos, não sobre a superfície da esfera (ou seja, se o eixo era (0,0,1) é linear em Z, não no ângulo azimutal). A função de iluminação esférica resultante é normalizada para que um ponto em uma superfície perfeitamente difusa sem sombreamento e um normal apontado na direção pDir resulte em radiação de saída com um valor de 1 (se a cor superior fosse branca e a cor inferior fosse preta). Este é um modelo muito simples onde Top representa a intensidade do "céu" e Bottom representa a intensidade do "chão".

Na esfera com raio de unidade, conforme mostrado na ilustração a seguir, a direção pode ser especificada simplesmente com theta, o ângulo sobre o eixo z na direção à direita e phi, o ângulo de z.

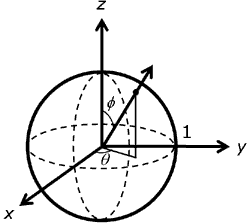
As equações a seguir mostram a relação entre as coordenadas cartesianas (x, y, z) e esféricas (theta, phi) na esfera de unidade. O ângulo theta varia acima do intervalo de 0 a 2 pi, enquanto phi varia de 0 a pi.

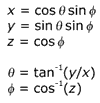
Requisitos

Requisito	Valor
parâmetro	D3dx9math.h
Biblioteca	D3dx9.lib

Confira também

Funções Matemáticas

Transferência de radiação pré-computada (Direct3D 9)