Теоретические основы поиска по алгоритму Гровера

В этой статье подробно описана теория математических принципов, на основе которых работает поиск по алгоритму Гровера.

Практическая реализация алгоритма Гровера для решения математических задач см. в разделе "Реализация алгоритма поиска Гровера".

Формулировка задачи

Алгоритм Гровера ускоряет решение для неструктурированных поисков данных (или проблемы поиска), выполняя поиск меньше, чем любой классический алгоритм. Любую задачу поиска можно выразить с помощью абстрактной функции $f(x)$, принимающей элементы поиска $x$. Если элемент $x$ является решением задачи поиска, $f(x)=1$. Если элемент $x$ не является решением, $f(x)=0$. Задача поиска состоит в поиске любого элемента $x_0$, для которого $f(x_0)=1$.

Действительно, любая проблема, которая позволяет проверить, является ли заданное значение $x$ допустимым решением ( &квор; Да или нет проблемы&кво;) можно сформулировать с точки зрения проблемы поиска. Ниже приводятся некоторые примеры:

• Логическая проблема удовлетворенности: соответствует ли набор логических значений $x$ интерпретации (назначение значений переменным), удовлетворяющих заданной логическому формуле?
• Проблема с продавцом: описывает ли $x$ самый короткий возможный цикл, соединяющий все города?
• Проблема поиска базы данных: содержит ли таблица базы данных запись $x$?
• Проблема целочисленной факторизации: является ли фиксированное число $N$ делимым числом по числу $x$?

Задачу, которую решает алгоритм Гровера, можно выразить следующим образом: для классической функции $f(x):\{0,1\}^n \rightarrow\{0,1\}$, где $n$ обозначает размер пространства поиска в битах, найти входное значение $x_0$, для которого $f(x_0)=1$. Сложность этого алгоритма определяется количеством использований функции $f(x)$. В классических вычислениях в худшем случае приходится определять значение $f(x)$ в общей сложности $N-1$ раз, где $N=2^n$, то есть отдельно проверять все возможности. После $N-1$ элементов должен быть последний элемент. Квантовый алгоритм Гровера может решить эту проблему намного быстрее, обеспечивая квадратичное ускорение. "Квадратичный" здесь означает, что потребуется всего $\sqrt{N}$ вычислений функции вместо прежних $N$.

Структура алгоритма

Предположим, есть $N=2^n$ подходящих элементов для задачи поиска, и они индексируются путем присвоения каждому элементу целого числа от $0$ до $N-1$. Далее предположим, что существует $M$ разных допустимых входных значений, что означает, что существует $M$ входных значений, для которых $f(x)=1$. Шаги алгоритма будут следующими:

1. Начните с регистра из $n$ кубитов, находящихся в состоянии $\ket{0}$.
2. Подготовьте для этого регистра равномерную суперпозицию, применив операцию $H$ к каждому кубиту регистра: $$|\text{регистр}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
3. Примените следующие операции к регистру $N_{\text{optimal}}$ times:
   1. Фазовый оракул $O_f$, который применяет условный сдвиг фазы $-1$ к элементам решения.
   2. Примените $H$ к каждому кубиту в регистре.
   3. Условный фазовый сдвиг $-1$ к каждому состоянию базиса вычислений, за исключением $\ket{0}$. Это можно представить в виде унитарной операции $-O_0$, так как $O_0$ представляет условный фазовый сдвиг только для $\ket{0}$.
   4. Примените $H$ к каждому кубиту в регистре.
4. Измерьте регистр, чтобы получить индекс элемента, который с очень высокой вероятностью является решением.
5. Проверьте, является ли это решение допустимым. Если нет, начните снова.

$N_\text{оптим.}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ обозначает оптимальное количество итераций, при котором достигается максимальная вероятность получения правильного элемента при измерении регистра.

Примечание.

Совместное применение шагов 3.b, 3.c и 3.d обычно известно в литературе как оператор диффузии Гровера.

Итоговая унитарная операция, примененная к регистру, выглядит так:

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{оптим.}}}H^{\otimes n}$$

Пошаговое отслеживание состояния регистра

Чтобы продемонстрировать этот процесс, давайте отследим все математические преобразования состояния регистра для простого примера, в котором используются всего два кубита и есть допустимый элемент $\ket{01}.$

1. Регистр начинается в состоянии: $$|\text{регистр}\rangle=|00\rangle$$

2. После применения $H$ к каждому кубиту его состояние изменится так: $$|\text{регистр}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$

3. Затем применяется оракул фазы и получается: $$|\text{регистр}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$

4. И еще раз применим $H$ для каждого кубита: $$|\text{регистр}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$

5. Теперь применим условный фазовый сдвиг ко всем состояниям, кроме $\ket{00}$: $$|\text{регистр}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$

6. Наконец, первая итерация Гровера заканчивается повторным применением $H$ и получается: $$|\text{регистр}\rangle=\ket{{01}$$

   Следуя вышеуказанным инструкциям, допустимый элемент можно найти за одну итерацию. Как вы увидите позже, это связано с N=4 и одним допустимым элементом, $N_\text{optimal}=1$.

Геометрическое объяснение

Чтобы понять, почему алгоритм Гровера дает нужный результат, давайте изучим его в геометрической форме. Пусть $\ket{\text{плохо}}$ описывает суперпозицию всех состояний, которые не являются решениями задачи поиска. Если существует $M$ допустимых решений, получим следующее:

$$\ket{\text{плохо}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

Состояние $\ket{\text{хорошо}}$ определяется как суперпозиция всех состояний, которые являются решением проблемы поиска:

$$\ket{\text{хорошо}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

Так как ни один элемент не может одновременно быть подходящим и неподходящим, хорошо и плохо являются взаимоисключающими множествами, а значит состояния $\ket{\text{хорошо}}$ и $\ket{\text{плохо}}$ ортогональны. Эти два состояния формируют ортогональный базис плоскости в векторном пространстве. С помощью этой плоскости мы можем визуализировать работу алгоритма.

Теперь предположим, что $\ket{\psi}$ является произвольным состоянием в пределах плоскости, сформированной состояниями $\ket{\text{хорошо}}$ и $\ket{\text{плохо}}$. Любое состояние в этой плоскости можно выразить так:

$$\ket{\psi}=\alpha\ket{\text{хорошо}} + \beta\ket{\text{плохо}}$$

где $\alpha$ и $\beta$ являются действительными числами. Теперь мы введем оператор отражения $R_{\ket{\psi}}$, где $\ket{\psi}$ представляет любое состояние кубитов в пределах заданной плоскости. Этот оператор определяется следующим образом:

$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$

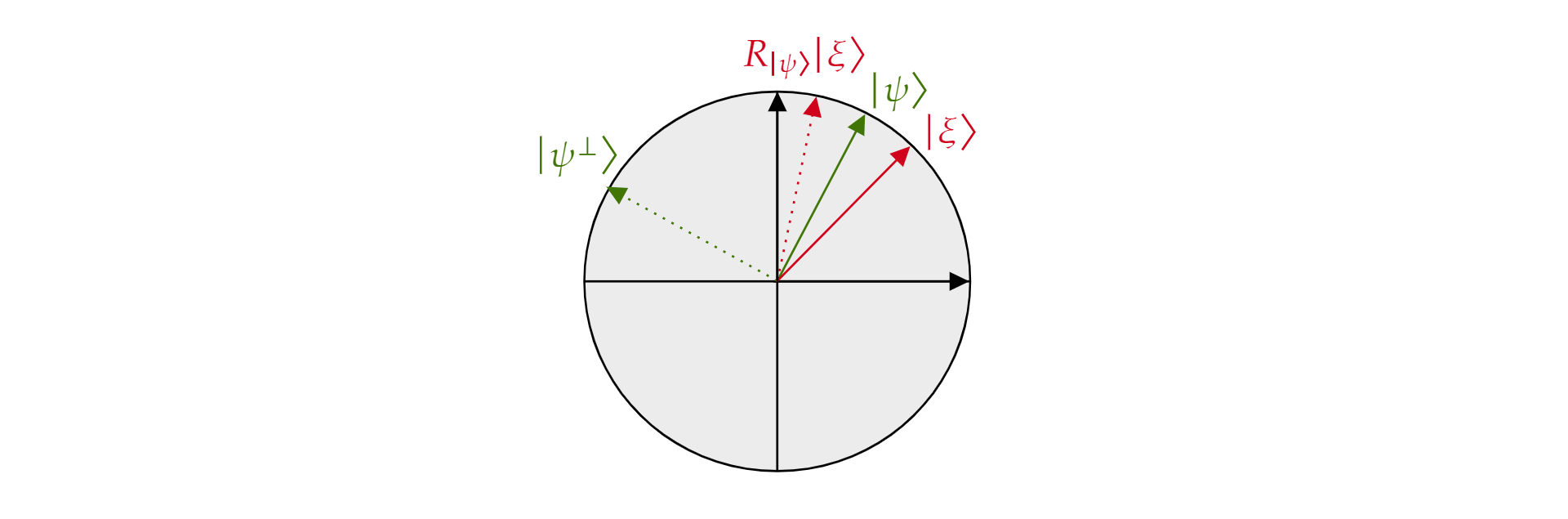
Он называется оператором отражения для $\ket{\psi}$, так как геометрически его можно представить как отражение направления $\ket{\psi}$. Для понимания этого возьмем ортогональный базис плоскости, сформированный $\ket{\psi}$, и ортогональное дополнение к нему $\ket{\psi^{\perp}}$. Любое состояние $\ket{\xi}$ в этой плоскости можно разложить по такому базису:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Если в одном из них используется оператор $R_{\ket{\psi}}$ для $\ket{\xi}$:

$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

Оператор $R_\ket{\psi}$ инвертирует компоненты, ортогональные к $\ket{\psi}$, но сохраняет неизменным компонент $\ket{\psi}$. Таким образом, $R_\ket{\psi}$ создает отражение относительно$\ket{\psi}$.

В алгоритме Гровера после первого применения $H$ к каждому кубиту получаем в качестве начального состояния равномерную суперпозицию всех состояний. Это можно записать так:

$$\ket{\text{все}}=\sqrt{\frac{M}{N}}\ket{\text{хорошо}} + \sqrt{\frac{N-M}{N}}\ket{\text{плохо}}$$

Таким образом, это состояние существует в пределах плоскости. Обратите внимание, что вероятность получения правильного результата при измерении из равной суперпозиции просто $|\braket{\text{хороша}|{\text{all}}}|^2=M/N$, что является то, что вы ожидаете от случайного предположения.

Оракул $O_f$ добавляет отрицательную фазу к каждому решению задачи поиска. Его можно записать как отражение относительно оси $\ket{\text{плохо}}$:

$$O_f = R_{\ket{\text{плохо}}}= 2\ket{\text{плохо}}\bra{\text{плохо}} - \mathcal{I}$$

Аналогичным образом, условный фазовый сдвиг $O_0$ по сути создает инвертированное отражение относительно состояния $\ket{0}$:

$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$

Зная об этом, можно легко убедиться, что операция диффузии Гровера $-H^{\otimes n} O_0 H^{\otimes n}$ также является отражением относительно состояния $\ket{все}$. Выполните такую операцию:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{все}}\bra{\text{все}} - \mathcal{I}= R_{\ket{\text{все}}}$$

Мы доказали, что каждая итерация алгоритма Гровера является сочетанием двух отражений: $R_\ket{\text{плохо}}$ и $R_\ket{\text{все}}$.

Совокупный результат каждой итерации Гровера аналогичен вращению угла $2\theta$ в направлении против часовой стрелки. К счастью, угол $\theta$ очень легко найти. Угол $\theta$ измеряется между известными направлениями $\ket{\text{все}}$ и $\ket{\text{плохо}}$, и его можно найти с помощью скалярного произведения. Известно, что $\cos{\theta}=\braket{\text{все}|\text{плохо}}$, поэтому необходимо вычислить $\braket{\text{все}|\text{плохо}}$. Разложение $\ket{\text{все}}$ по векторам $\ket{\text{плохо}}$ и $\ket{\text{хорошо}}$ дает следующее:

$$\theta = \arccos{\left(\braket{\text{все}|\text{плохо}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

Угол между состоянием регистра и $\ket{\text{хорошим}}$ состоянием уменьшается при каждой итерации, что приводит к повышению вероятности измерения допустимого результата. Чтобы вычислить эту вероятность, просто необходимо вычислить $|\braket{\text{хороший}|\text{регистр}}|^2$. Обозначив угол между $\ket{\text{хорошо}}$ и $\ket{\text{регистр}}$$\gamma как (k)$, где $k$ соответствует числу итераций, получим следующее:

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

А это означает, что вероятность успешного измерения составляет:

$$P(\text{успех}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

Оптимальное число итераций

Так как вероятность успешного поиска можно выразить как функцию от числа итераций, мы можем найти оптимальное число итераций $N_{\text{оптим.}}$, найдя наименьшее натуральное число, которое (приближенно) дает максимальную вероятность успеха для функции.

Известно, что $\sin^2{x}$ достигает своего первого максимума при $x=\frac{\pi}{2}$, поэтому:

$$\frac{\pi}{{2}=(2k_{\text{оптим.}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Результат выполнения команды:

$$k_{\text{оптим.}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$

Где на последнем шаге $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.

Поэтому вы можете выбрать $N_optimal, чтобы быть $N_\text{\text{optimal}=}$\left\lfloor \pi{4}\sqrt{\frac{}{N M}}}{-\frac{{1}{2}\right\rfloor.\frac{$

Анализ сложности

Из предыдущего анализа известно, что $O\left(\sqrt{\frac{N}{M}}\right)$ запросов оракула $O_f$ необходимо, чтобы найти допустимый элемент. Но можно ли реализовать этот алгоритм эффективно по критерию затрат времени? $O_0$ основывается на вычислении логических операций по $n$ битов и гарантированно выполняется с использованием $O(n)$ вентилей. Есть также два уровня $n$ вентилей Адамара. Для обоих этих компонентов потребуется не более $O(n)$ вентилей на каждую итерацию. Поскольку $N=2^n$, отсюда следует, что $O(n)=O(log(N))$. Это означает, что потребуется $O\left(\sqrt{\frac{N}{M}}\right)$ итераций, по $O(log(N))$ вентилей на каждую, а общая сложность по времени (без учета затрат на реализацию оракула) составляет $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.

Общая сложность алгоритма в конечном счете зависит от сложности реализации O_f$ oracle$. Если оценка функции гораздо сложнее на квантовом компьютере, чем на классическом, общая среда выполнения алгоритма будет длиннее в квантовом случае, хотя технически, она использует меньше запросов.

Ссылки

Дополнительные сведения об алгоритме Гровера можно получить в любом из следующих источников:

• Оригинальная работа Лова К. Гровера
• Раздел алгоритмов квантового поиска Nielsen, M. A. &ампер; Чуанг, И. Л. (2010). Quantum Computation and Quantum Information.
• Алгоритм Гровера на Arxiv.org

Связанный контент

• Запутанность в квантовых вычислениях
• Векторы и матрицы
• T ворота и фабрики T
• Несколько кубитов