Kuantum devresi diyagramı kuralları

Bazen kuantum algoritmalarını bir devre diyagramında anlamak, eşdeğer yazılı matris gösterimine göre daha kolaydır. Bu makalede kuantum devresi diyagramlarının ve kurallarının nasıl okunduğu açıklanmaktadır.

Daha fazla bilgi için bkz . Kuantum devreleri diyagramlarını görselleştirme.

Kuantum devresi diyagramlarını okuma

Kuantum devresinde zaman soldan sağa doğru akar. Kuantum geçitleri, en soldaki geçidin kubitlere ilk uygulanan geçit olduğu kronolojik sırayla sıralanır.

Örnek olarak aşağıdaki kuantum devresi diyagramını alın:

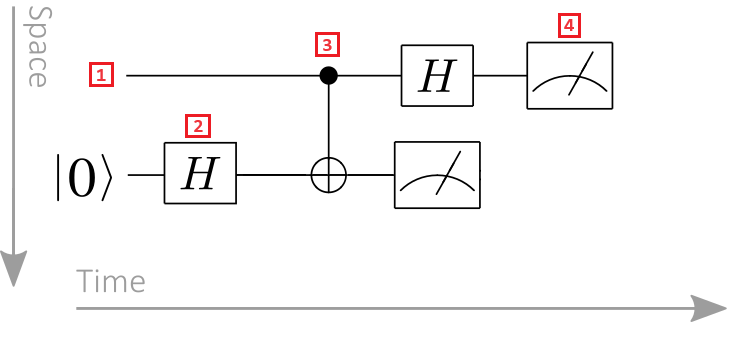
1. Kubit yazmaç: Kubit yazmaçları yatay çizgiler olarak görüntülenir ve her satır bir kubiti temsil eder. Üst satır, 0 etiketiyle belirtilmiş kubit yazmacıdır, ikinci satır ise 1 etiketiyle belirtilmiş kubit yazmacıdır ve bu şekilde devam eder.
2. Kuantum kapısı: Kuantum işlemleri, kuantum geçitleri tarafından temsil edilir. Kuantum kapısı terimi klasik mantık kapılarına benzer. Bir veya daha fazla kubit yazmaç üzerinde hareket eden geçitler kutu olarak belirtilir. Bu örnekte, simgesi hadamard işlemini temsil eder.
3. Kontrollü kapı: Kontrollü kapılar iki veya daha fazla kubit üzerinde hareket eder. Bu örnekte, simge bir CNOT geçidini temsil etti. Siyah daire denetim kubitini, daire içindeki çarpı ise kubiti target temsil eder.
4. Ölçüm işlemi: Ölçüm simgesi bir ölçüm işlemini temsil eder. Ölçüm işlemi giriş olarak bir kubit yazmaç alır ve klasik bilgileri çıkarır.

Kuantum geçitlerini uygulama

Zaman soldan sağa doğru aktığı için en soldaki geçit önce uygulanır. Örneğin, aşağıdaki kuantum devresinin eylemi ünitermatris $CBA$'dır.

Not

Matris çarpması karşıt kurala uyar: önce en sağdaki matris uygulanır. Ancak kuantum devresi diyagramlarında önce en soldaki kapı uygulanır. Bu fark bazen karışıklığa yol açabilir, bu nedenle doğrusal cebirsel gösterimi ile kuantum devresi diyagramları arasındaki bu önemli farkı not etmek önemlidir.

Kuantum devrelerinin girişleri ve çıkışları

Kuantum devresi diyagramında, kuantum kapısına giren kablolar kuantum kapısına giriş olan kubitleri, kuantum geçidinden çıkan kablolar ise kuantum geçidinden çıkan kubitleri temsil eder.

Kuantum kapısı girişlerinin sayısı, kuantum geçidinin çıktı sayısına eşittir. Bunun nedeni kuantum işlemlerinin ünitesel olması ve dolayısıyla geri döndürülebilir olmasıdır. Bir kuantum kapısı girişlerden daha fazla çıkışa sahipse, geri alınamaz ve bu nedenle üniter olmaz, bu bir çelişkidir.

Bu nedenle, bir devre diyagramında çizilen herhangi bir kutuya giren ve çıkan kablo sayısının tam olarak aynı olması gerekir.

Çok kubitli işlemler

Çok kubitli devre diyagramları, tek kubitli diyagramlara benzer kuralları izler. Örneğin, iki kubitli birim işlem $B$ (H S$ X)\otimes olarak $tanımlanabilir, dolayısıyla eşdeğer kuantum devresi aşağıdaki gibidir:

$B$'yi, devrenin kullanıldığı bağlama bağlı olarak, iki adet tek-kubitli yazmaç yerine tek bir iki-kubitli yazmaç üzerinde bir eyleme sahip olarak da görüntüleyebilirsiniz.

Bu tür soyut devre diyagramlarının belki de en kullanışlı özelliği, karmaşık kuantum algoritmalarının temel geçitlere kadar derlemek zorunda kalmadan üst düzeyde açıklanmasıdır. Bu, algoritma içindeki alt yordamların her birinin nasıl çalıştığına ilişkin tüm ayrıntıları anlamanıza gerek kalmadan büyük bir kuantum algoritması için veri akışı hakkında bir sezgi elde edebilirsiniz.

Kontrollü kapılar

Kuantum denetimli geçitler, bir denetim kubiti belirli bir durumdaysa kubite target tek kubitli bir geçit uygulayan iki kubitli geçitlerdir.

Örneğin, tek bir kubitin değeri $\LambdaG$ işleminin uygulanmasını kontrol ettiği $(G)$olarak belirtilen kuantum kontrollü bir kapıyı düşünün. Denetimli kapı $\Lambda(G),$ aşağıdaki ürün durumu girişi örneğine bakılarak anlaşılabilir:

$$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi}+ G \beta\ket{{1}\ket{\psi}$$

Başka bir ifadeyle, denetim kubiti yalnızca değeri $1$ olduğunda, denetimli kapı $\psi$ yazmacına $G$ uygular. Genel olarak, bu denetimli işlemler devre diyagramlarında aşağıdaki sembolle açıklanmıştır:

Burada siyah daire, geçidin denetlendiği kuantum bitini, dikey bir tel ise denetim kubiti 1$ değerini $aldığında uygulanan üniteyi belirtir.

Özel durumlar için $G=X$ ve $G=Z$, kapıların kontrol edilen versiyonunu tanımlamak için aşağıdaki gösterim kullanılır (kontrollü X kapısı CNOT kapısıdır):

Q#, bir işlemin denetimli sürümünü otomatik olarak oluşturmak için yöntemler sağlar ve bu da programcının bu işlemleri el ile kodlamak zorunda kalmamasını sağlar. Bunun bir örneği aşağıda gösterilmiştir:

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

Klasik kontrollü kapılar

Kuantum geçitleri, ölçümün sonucunun klasik bir denetim biti işlevi gördüğü bir ölçümden sonra da uygulanabilir.

Aşağıdaki simge, klasik olarak kontrol edilen bir kapıyı temsil eder; burada $G$, klasik kontrol bitinin $1$ değerine göre uygulanır.

Ölçüm operatörü

Ölçüm işlemleri bir kubit yazmaç alır, bunu ölçer ve sonucu klasik bilgi olarak çıkartır.

Ölçüm işlemi bir ölçüm simgesiyle gösterilir ve her zaman bir kubit yazmaç girişi olarak alır (düz çizgiyle gösterilir) ve klasik bilgileri (çift çizgiyle gösterilir) çıkarır. Özellikle, ölçüm işleminin simgesi şöyle görünür:

Q# içinde Measureişleci ölçüm işlemini uygular.

Örnek: Birimsel dönüşüm

CNOT$\text{_}(H{01} 1)\otimes$ünitesel dönüştürmeyi göz önünde bulundurun. Bu geçit dizisi, en üst düzeyde dolanık iki kubitli bir durum oluşturduğundan kuantum bilişimi için temel öneme sahiptir:

$$\text{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}} (\ket{{00} + \ket{11})$$

Bu veya daha karmaşık olan işlemler kuantum algoritmalarında ve kuantum hata düzeltmesinde yaygın olarak bulunur.

Bu dolanık kuantum durumunu hazırlamak için devre diyagramı şu şekildedir:

Hadamard kapısının arkasındaki simge, siyah dairenin kontrol kubitini, daire içindeki çarpının ise target kubitini gösterdiği bir CNOT kapısını temsil eder. Bu kuantum devresi iki kubit (veya bir kubitten oluşan eşdeğer iki yazmaç) üzerinde hareket ediyor olarak gösterilir.

Örnek: ışınlanma devresi diyagramı

Kuantum ışınlaması, devre bileşenlerinin gösterilmesi için en iyi kuantum algoritmalarından biridir.

Kuantum ışınlaması, bir kuantum durumunun, gönderen ve alıcı arasında paylaşılan dolanık durum ve bunlar arasındaki klasik iletişim yardımıyla bir kubitten diğerine iletilmesini sağlayan bir protokoldür.

Öğrenme amacıyla gönderene Alice, alıcı Bob, ışınlanacak kubite ise ileti kubiti adı verilir. Alice ve Bob her biri bir kubit tutar ve Alice'in ileti kubiti olan ek bir kubiti vardır.

Aşağıdaki devre diyagramında ışınlama protokolü gösterilmektedir:

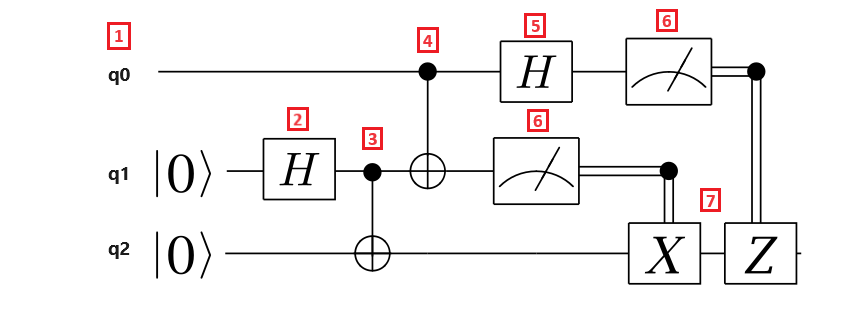
Işınlama protokolünün adımlarını ayıralım:

1. Kubit yazmaç q0 ileti kubiti, kubit yazmaç q1 Alice'in kubiti ve kubit yazmaç q2 ise Bob'un kubitidir. Mesaj kubiti bilinmeyen bir durumda ve Alice ve Bob'ın kubitleri $\ket{0}$ durumunda.
2. Alice'in kubitine bir Hadamard kapısı uygulanır. Çünkü kubit $\ket{0}$ durumunda olduğundan, sonuçta elde edilen durum $\frac{1}{\sqrt{{2}}(\ket{{0} + \ket{1})$ olur.
3. CNOT kapısı, Alice ve Bob'ın kubitlerine uygulanır. Alice'in kubiti denetim kubiti, Bob'ın kubiti ise kubittir target . Sonuçta elde edilen durum ($\frac{ + {1}{\sqrt{2}}\ket{00})\ket{'dir{11}$. Alice ve Bob artık dolanık bir durumu paylaşıyorlar.
4. CNOT kapısı, ileti kubiti ve Alice'in kubiti üzerine uygulanır. Alice'in kubiti de Bob'un kubitiyle dolanık olduğundan, sonuçta elde edilen durum üç kubit dolanık bir durumdur.
5. İleti kubitine bir Hadamard kapısı uygulanır.
6. Alice iki kubitini ölçer ve ölçüm sonuçlarını Bob'a söyler, ancak bu devreye yansıtılmamaktadır. Ölçüm sonuçları 00, 01, 10 veya 11 değerlerini alabilen iki klasik bittir.
7. Pauli kapıları X ve Z, sonuç bitinin 1 değerine bağlı olarak Bob'un kübitine klasik olarak uygulanır. Sonuçta elde edilen durum, özgün ileti kubit durumudur.

İlgili içerik

• Kuantum dolanıklığı
• Grover algoritması
• Kuantum Ara Gösterimi
• Vektörler ve matrisler