Grover'ın arama algoritması teorisi

Bu makalede Grover algoritmasının çalışmasını sağlayan matematiksel ilkelerin ayrıntılı teorik açıklamasını bulacaksınız.

Grover algoritmasının matematiksel sorunları çözmeye yönelik pratik bir uygulaması için bkz . Grover arama algoritmasını uygulama.

Sorunun açıklaması

Grover algoritması, aramayı klasik algoritmalardan daha az adımda çalıştırarak yapılandırılmamış veri aramalarına (veya arama sorununa) yönelik çözümü hızlandırır. Herhangi bir arama görevi, x arama öğelerini$$ kabul eden bir soyut f(x)$ işleviyle $ifade edilebilir. x$ öğesi $arama görevinin $çözümüyse f(x)=1$. x$ öğesi $bir çözüm değilse f$(x)=0$. Arama sorunu, f(x_0)=1$ gibi $x_0$ herhangi bir öğeyi $bulmaktan oluşur.

Gerçekten de, belirli bir x$ değerinin $geçerli bir çözüm olup olmadığını denetlemenize olanak tanıyan herhangi bir sorun (&bir quot; evet veya hayır sorun") arama sorunu açısından formüle edilebilir. Aşağıda bazı örnekler verilmiştir:

• Boole doyumlanabilirliği sorunu: Boole değerleri $$ kümesi, verilen Boole formülünü karşılayan bir yorum mu (değişkenlere değer ataması) ?
• Seyahat eden satıcı sorunu: x$, tüm şehirleri birbirine bağlayan mümkün olan en kısa döngünün ne olduğunu açıklıyor mu$?
• Veritabanı arama sorunu: Veritabanı tablosu x$ kaydı $içeriyor mu?
• Tamsayı çarpanları belirleme sorunu: Sabit N$ sayısı x$ sayısına $$göre bölünebiliyor mu?

Grover algoritmasının çözmeyi hedeflediği görev şu şekilde ifade edilebilir: klasik bir işlev $olan f(x):\0,1\{}^n \rightok\{0,1\}$; burada $n$ arama alanının bit boyutudur, f(x_0)=1$ için $bir giriş $x_0$ bulun. Algoritmanın karmaşıklığı f(x)$ işlevinin $kullanım sayısıyla ölçülür. Klasik olarak, en kötü durum senaryosunda $f(x)$ toplam $N-1$ kez değerlendirilmelidir; burada $N=2^n$, tüm olasılıklar denenmektedir. N-1$ öğeden sonra $son öğe olmalıdır. Grover'ın kuantum algoritması bu sorunu çok daha hızlı çözebilir ve ikinci dereceden bir hız sağlar. Burada ikinci dereceden, N ile karşılaştırıldığında$$ yalnızca N}$ değerlendirmesinin $\sqrt{gerekli olacağı anlamına gelir.

Algoritmanın özeti

Arama görevi için N=2^n$ uygun öğe olduğunu $ve her öğeye 0'dan $$ N-1'e $$bir tamsayı atayarak dizine alındıklarını varsayalım. Ayrıca, M farklı geçerli girişler olduğunu $varsayalım; yani f(x)=1$ için $M$ girişleri vardır$.$ Ardından algoritmanın adımları aşağıdaki gibidir:

1. durumunda $\ket{0}$başlatılan n$ kubit yazmaç $ile başlayın.
2. Yazmaç her kubitine H uygulayarak $kaydı tekdüzen bir süper pozisyona hazırlayın: $$|\text{register}\rangle=\frac{1}{\sqrt{N\sum}}_{x=0}^{N-1}|x$\rangle$$
3. Yazmaç $N_{\text{ en iyi}}$ zamanlara aşağıdaki işlemleri uygulayın:
   1. Aşama kahini$,$ çözüm öğeleri için -1$ koşullu faz kaydırması $uygulayan O_f.
   2. Kayıttaki her kubite H$ uygulayın$.
   3. -1'in $$ koşullu fazdan hariç $\ket{0}$her hesaplama temeli durumuna kayması. Bu, -O_0 birim işlemiyle $temsil edilebilir, O_0$ $yalnızca koşullu aşama kaydırmasını $\ket{0}$ temsil eder.$
   4. Kayıttaki her kubite H$ uygulayın$.
4. Çok yüksek olasılıkla çözüm olan bir öğenin dizinini almak için yazmaç değerini ölçün.
5. Geçerli bir çözüm olup olmadığını denetleyin. Aksi takdirde yeniden başlayın.

$\text{N_optimal=}\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{2}\frac{1}{\right\rfloor$, kaydı ölçerek doğru öğeyi alma olasılığını en üst düzeye çıkaran en uygun yineleme sayısıdır.

Not

3.b, 3.c ve 3.d adımlarının ortak uygulaması genellikle literatürde Grover'un difüzyon operatörü olarak bilinir.

Yazmaç için uygulanan genel birim işlemi:

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

Kaydın durumunu adım adım takip edin

İşlemi göstermek için, yalnızca iki kubitin bulunduğu ve geçerli öğenin $\ket{01}olduğu basit bir durum için yazmaç durumunun matematiksel dönüşümlerini takip edelim.$

1. Yazmaç şu durumda başlar: $$|\text{kayıt}\rangle=|00\rangle$$

2. Her kubite H uygulandıktan $sonra yazmaç şu duruma dönüşür: $$|\text{register={4}}}\rangle\frac{\sum{1}{\sqrt{_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}++)\ket{10}\ket{11}$$$

3. Ardından, aşama kahini şu bilgileri almak için uygulanır: $$|\text{register}\rangle=\frac12({00}\ket{-{01}\ket{++)\ket{\ket{{10}{11}$$

4. Ardından $H$, her kubit üzerinde yeniden hareket eder ve verir: $$|\text{register}\rangle\frac=12(\ket{{00}+\ket{{01}-{10}\ket{+)\ket{{11}$$

5. Artık koşullu aşama kaydırması şu durumlar dışında $\ket{00}$her duruma uygulanır: $$|\text{register}\rangle\frac=12(\ket{{00}-\ket{{01}+{10}\ket{-)\ket{{11}$$

6. Son olarak, ilk Grover yinelemesi şunu almak için yeniden H$ uygulanarak $sona erer: $$|\text{register}\rangle=\ket{{01}$$

   Yukarıdaki adımları izleyerek geçerli öğe tek bir yinelemede bulunur. Daha sonra göreceğiniz gibi, bunun nedeni N=4 ve tek bir geçerli öğe ( $N_\text{optimal}=1$) içindir.

Geometrik açıklama

Grover algoritmasının neden çalıştığını görmek için geometrik bir perspektiften algoritmayı inceleyelim. Arama $\ket{\text{sorununa çözüm olmayan tüm durumların süper konumu kötü}}$ olsun. M$ geçerli çözümleri olduğunu $varsayalım:

$$\ket{\text{hatalı}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

İyi durum$\ket{\text{}}$, arama sorununa çözüm olan tüm durumların süper konumu olarak tanımlanır:

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

bir öğe geçerli ve geçerli olmadığından iyi ve kötü birbirini dışlayan kümeler olduğundan, iyi}}$ ve $\ket{\text{kötü}}$ durumları $\ket{\text{ortogonaldir. Her iki durum da vektör uzayında bir düzlemin ortogonal temelini oluşturur. Algoritmayı görselleştirmek için bu düzlemi kullanabilirsiniz.

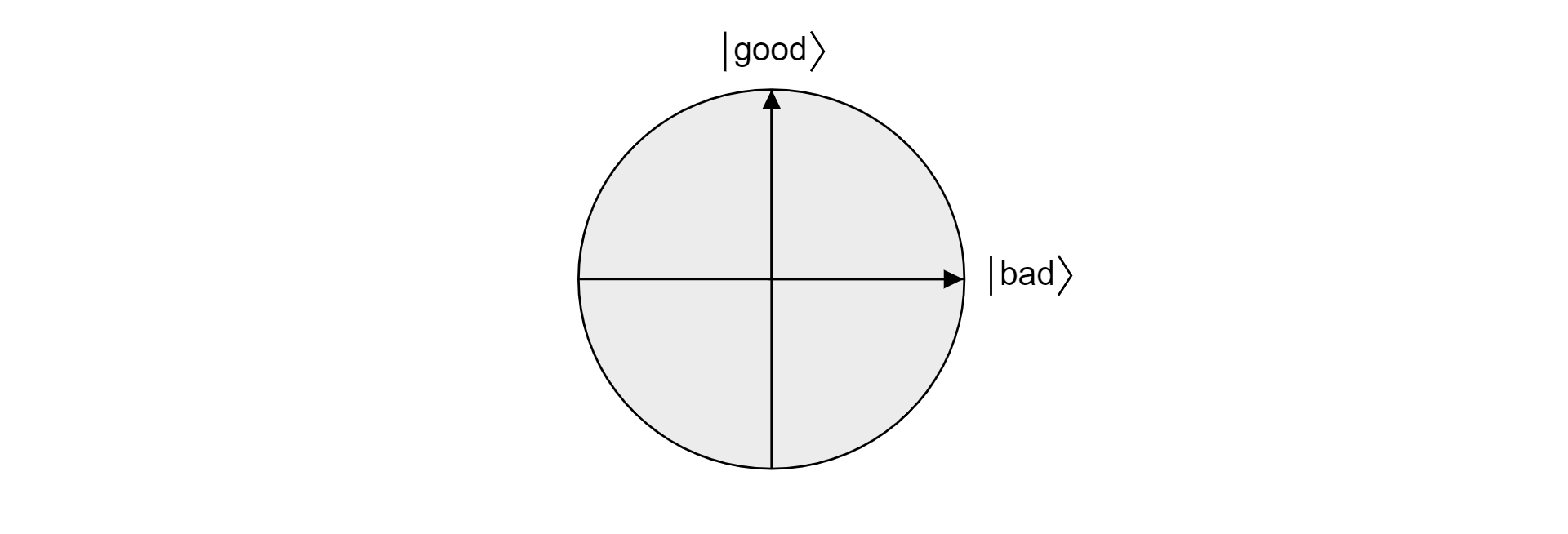
Şimdi, uçakta iyi ve kötü}}$ tarafından yayılan $\ket{\text{rastgele bir durum olduğunu varsayalım$\ket{\psi}$.$\ket{\text{}}$ Bu uçakta yaşayan tüm eyaletler şu şekilde ifade edilebilir:

$$\ket{\psi}=\alpha\ket{\text{iyi}} + \beta\ket{\text{kötü}}$$

$\beta$ ve $\alpha$ gerçek sayılardır. Şimdi R_ yansıma işlecini ${\ket{\psi}}$tanıtalım. $\ket{\psi}$ Burada uçakta herhangi bir kubit durumu yaşanacak. işleç şu şekilde tanımlanır:

$${\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$

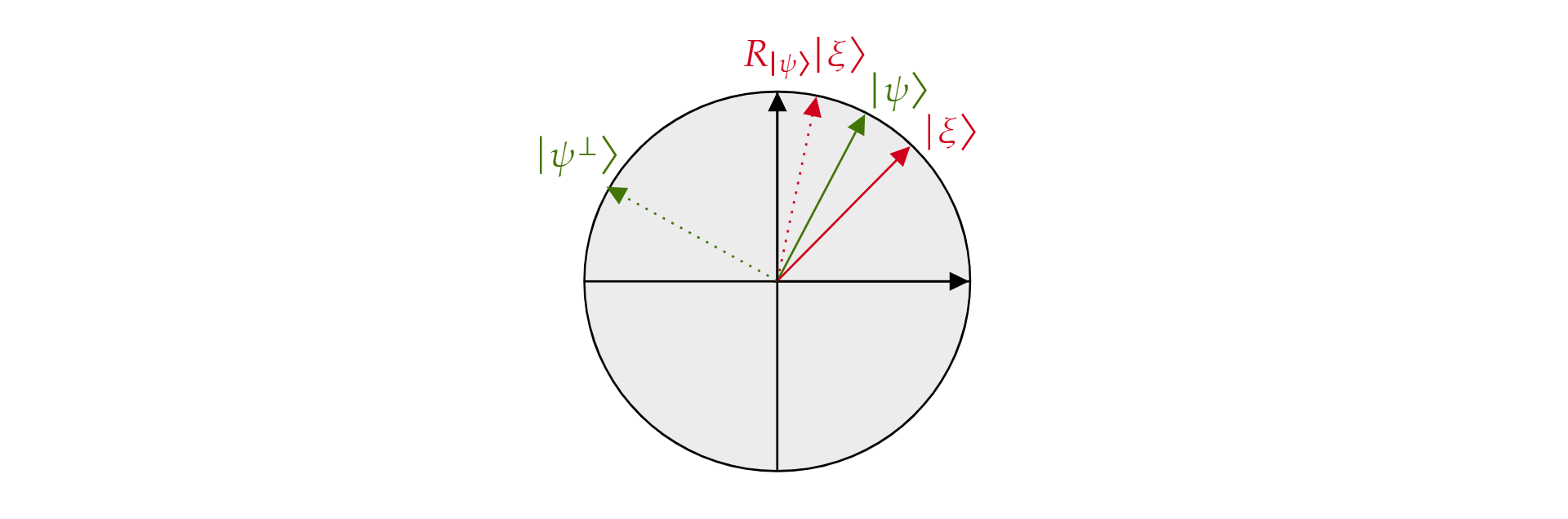
Geometrik olarak yönü hakkında yansıma olarak yorumlanabildiği için, bu, hakkında $\ket{\psi}$ $\ket{\psi}$yansıma işleci olarak adlandırılır. Bunu görmek için, tarafından oluşturulan $\ket{\psi}$ düzlemin ortogonal temelini ve ortogonal tamamlayıcısı $\ket{\psi^{\perp}}$ alın. Düzlemin herhangi bir durumu $\ket{\xi}$ şu şekilde ayrıştırılabilir:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Biri \xi}$ için işleç $R_{\ket{\psi}}$ $\ket{uygularsa:

$${\ket{\psi}}\ket{R_\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

operatör $R_\ket{\psi}$ bileşeni ortogonal olarak $\ket{\psi}$ ters çevirir ancak bileşeni değişmeden bırakır $\ket{\psi}$ . Bu nedenle, $R_\ket{\psi}$ hakkında $\ket{\psi}$bir yansımadır.

Grover algoritması, H'nin$ her kubite ilk uygulanmasından $sonra tüm eyaletlerin tekdüzen süper pozisyonuyla başlar. Bu şu şekilde yazılabilir:

$$\ket{\text{tüm}}\sqrt{\frac{=M}{N}}\ket{\text{iyi}} + \sqrt{\frac{N-M}{N}}\ket{\text{kötü}}$$

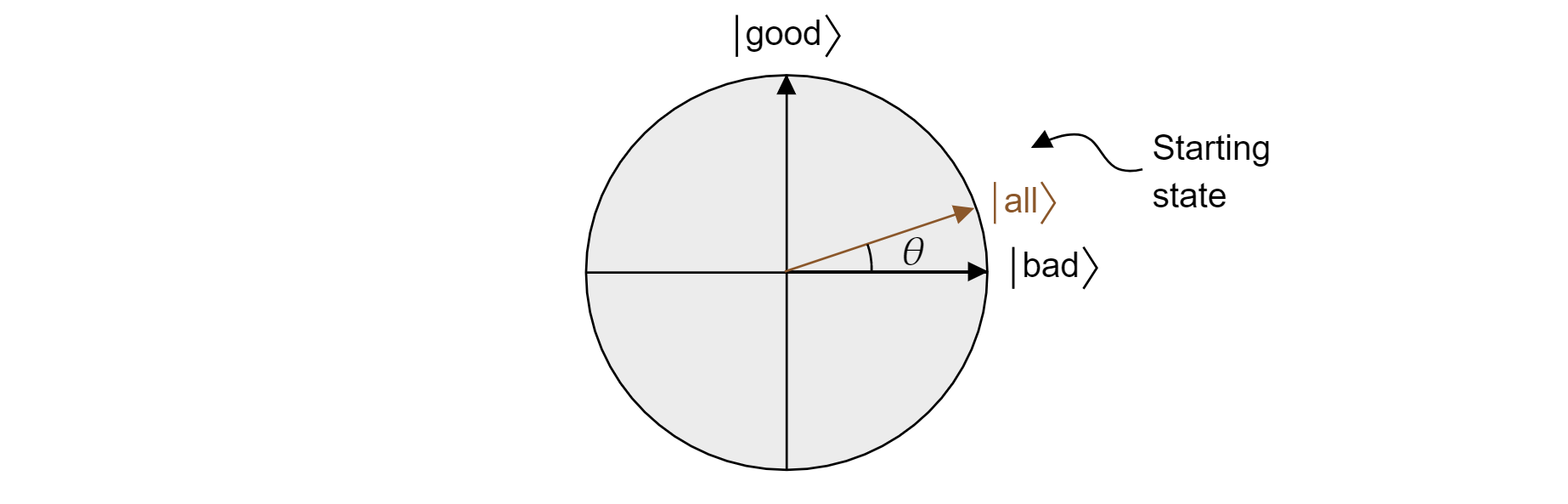
Ve böylece devlet uçakta yaşıyor. Eşit süper pozisyondan ölçüm yaparken doğru bir sonuç elde etme olasılığının yalnızca $|\braket{\text{iyi}}}|}|{\text{ olduğunu unutmayın^2=M/N$, rastgele bir tahminden bekleyebileceğiniz şey budur.

Oracle $O_f$ , arama sorununun herhangi bir çözümüne olumsuz bir aşama ekler. Bu nedenle, hatalı}}$ eksen hakkında $\ket{\text{bir yansıma olarak yazılabilir:

$$= O_f R_{\ket{\text{bad=}}} 2\ket{\text{bad}}\bra{\text{}} - \mathcal{I}$$

Benzer şekilde, koşullu faz kaydırma $O_0$ durumu $\ket{0}$hakkında yalnızca ters bir yansımadır:

$$O_0 R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I =}$$

Bu olguyu bilerek Grover difüzyon işleminin $-H^{\otimes n} O_0 H^{\otimes n}$ işleminin de durumla $\ket{}$ilgili bir yansıma olduğunu denetlemek kolaydır. Yalnızca şunu yapın:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^ n H^{\otimes{\otimes n}}\ket{0}\bra{{0} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{}} - \mathcal{I}= R_all{\ket{\text{}}}$$

Grover algoritmasının her yinelemesinin, R_bad}}$ ve $R_\ket{\text{all}}$ olmak R_\ket{\text{ iki yansımanın $bileşimi olduğu gösterilmiştir.

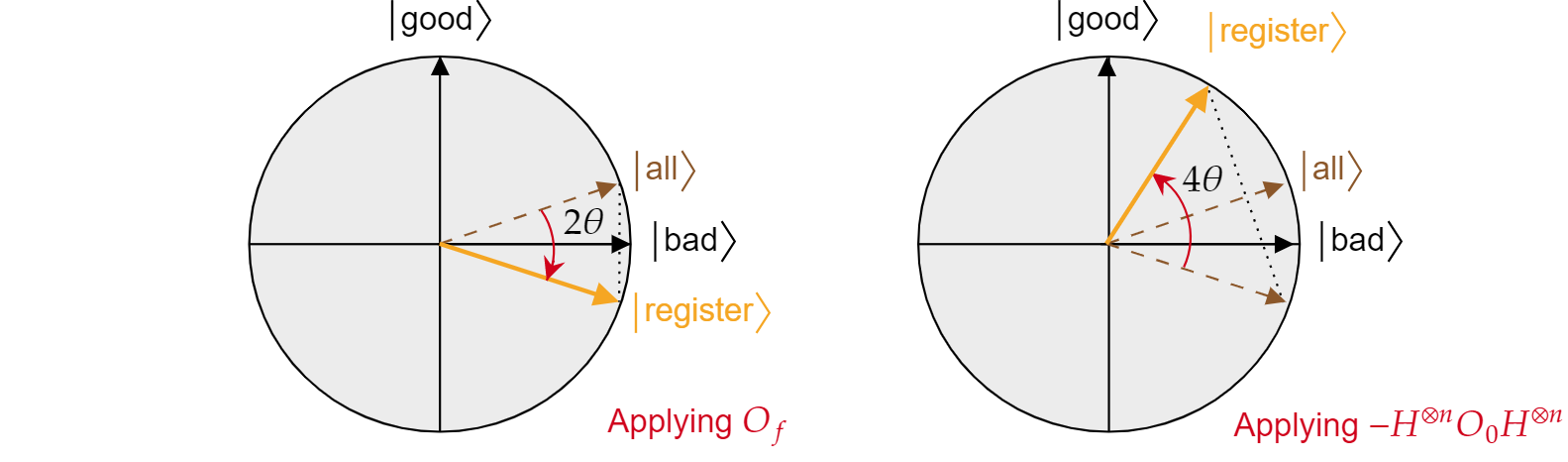
Her Grover yinelemesinin birleşik etkisi, 2\theta$ açısını $saat yönünün tersine döndürmedir. Neyse ki \theta$ açısını $bulmak kolaydır. \theta$ yalnızca tüm}}$ ve $\ket{\text{kötü}}$ arasındaki $\ket{\text{açı olduğundan$, açıyı bulmak için skaler ürünü kullanabilirsiniz. \cos{\theta'nın}=\braket{\text{tamamen}|\text{kötü}}$ olduğu bilinmektedir$, bu nedenle tüm}|\text{kötü}}$ değerlerin hesaplanması $\braket{\text{gerekir. Kötü ve $\ket{\text{iyi}}$ açısından tümünün $\ket{\text{}}$ ayrıştırmasından}}$ $\ket{\text{şu şekildedir:

$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

Yazmaç durumu ile $\ket{\text{iyi}}$ durum arasındaki açı her yinelemede azalır ve bu da geçerli bir sonucu ölçme olasılığının daha yüksek olmasına neden olur. Bu olasılığı hesaplamak için iyi bir yazmaç}}|^2$ hesaplamanız}|\text{$|\braket{\text{ yeterlidir. good}}$ ve $\ket{\text{register$\gamma}}$ (k)$ arasındaki $\ket{\text{açıyı belirten, burada $k$ yineleme sayısıdır:

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

Bu nedenle başarı olasılığı şu şekildedir:

$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

En iyi yineleme sayısı

Başarı olasılığı, yineleme sayısının bir işlevi olarak yazılabildiği için, başarı olasılığı işlevini en üst düzeye çıkaran en küçük pozitif tamsayı hesaplanarak en uygun yineleme $sayısı N_{\text{optimal}}$ bulunabilir.

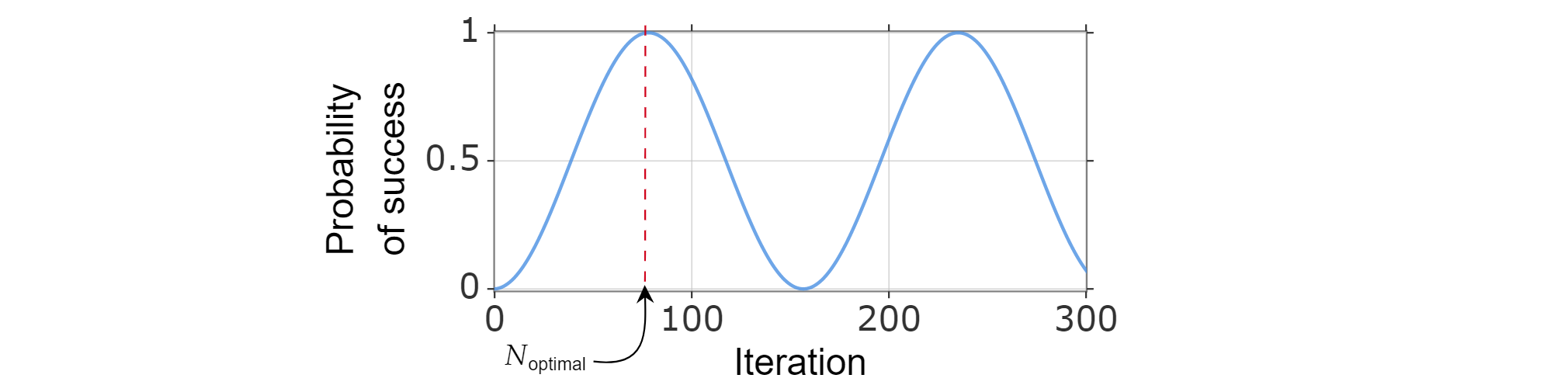
\sin^2{x'in $x=\frac{}$\pi}{2}$ için $ilk üst sınırına ulaştığı bilinmektedir, bu nedenle:

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Bu, şunu verir:

$${\text{k_optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi{4}\sqrt{\frac{}{N}{M-O}}\frac{1}{2}\left(\sqrt\frac{M}{N)}\right$$

Burada son adımda , $\arccos \sqrt{1-x=\sqrt{}x} + O(x^{3/2})$.

Bu nedenle, N_optimal öğesini N_\text{optimal\left}=\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{1}{2}\frac{\right\rfloor$ olarak $seçebilirsiniz.$}$\text{

Karmaşıklık analizi

Önceki analizde geçerli $bir öğeyi bulmak için kahin $O_f$ O\left(\sqrt{\frac{N}{M}}\right)$ sorguları gerekir. Ancak algoritma, zaman karmaşıklığı açısından verimli bir şekilde uygulanabilir mi? $$ O_0, n$ bit üzerinde $Boole işlemlerini hesaplamayı temel alır ve O(n)$ geçitleri kullanılarak $uygulanabilir olduğu bilinmektedir. Ayrıca iki katman $n$ Hadamard kapısı vardır. Bu nedenle bu bileşenlerin her ikisi de yineleme başına yalnızca $O(n)$ geçitleri gerektirir. N=2^n$ olduğundan$, O$(n)=O(log(N))$ değerini izler. Bu nedenle, $yineleme başına O\left(\sqrt{\frac{N}{M}}\right)$ yinelemeleri ve $O(günlük(N))$ geçitleri gerekiyorsa, toplam zaman karmaşıklığı (oracle uygulamasını hesaba katmadan) O\left(\sqrt{\frac{N}{M}}günlüğü(N)\right)$ olur$.

Algoritmanın genel karmaşıklığı, oracle $O_f$ uygulamasının karmaşıklığına bağlıdır. Bir işlev değerlendirmesi kuantum bilgisayarda klasik bir bilgisayara göre çok daha karmaşıksa, teknik olarak daha az sorgu kullansa da genel algoritma çalışma zamanı kuantum durumunda daha uzun olacaktır.

Başvurular

Grover algoritması hakkında bilgi edinmeye devam etmek istiyorsanız aşağıdaki kaynaklardan herhangi birini de kontrol edebilirsiniz:

• Orijinal kağıt: Lov K. Grover
• Nielsen, M. A.'nın kuantum arama algoritmaları bölümü. &Amp; ^ Chuang, I. L. (2010). Kuantum Hesaplaması ve Kuantum Bilgileri.
• grover algoritması Arxiv.org

İlgili içerik

• Kuantum bilişiminde dolanıklık
• Vektörler ve matrisler
• T kapıları ve T fabrikaları
• Birden çok kubit